Інженеру часто доводиться вирішувати алгебраїчні та трансцендентні рівняння, що може представляти собою самостійну задачу чи є складовою частиною більш складних задач. В обох випадках практична цінність чисельного методу в значній мірі визначається швидкістю та ефективністю отримання розв’язку. Вибір необхідного алгоритму для розв’язку рівнянь залежить від характеру задачі, яка розглядається. Розглянемо основні теоретичні поняття та практичні рекомендації при розв’язку нелінійних рівнянь на ЕОМ.
При вирішенні практичних інженерних задач часто доводиться зустрічатися з розв’язанням рівнянь виду
![]() , (4.1)
, (4.1)
або ![]() (4.2)
(4.2)
де ![]() ,
, ![]() та
та ![]() – нелінійні функції, визначенні на деякій числовій множині
– нелінійні функції, визначенні на деякій числовій множині ![]() , яка називається областю допустимих значень рівняння.
, яка називається областю допустимих значень рівняння.
Рівняння виду (4.1) або (4.2) називаються нелінійними рівняннями. Всі нелінійні рівняння можна поділити на алгебраїчні та трансцендентні (рис.4.1)
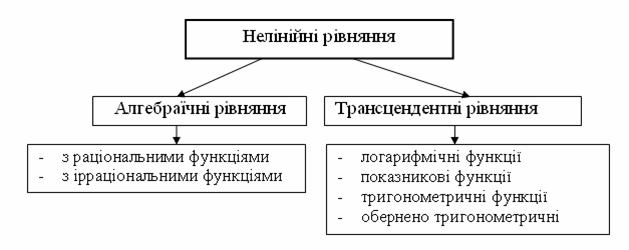
Рисунок 4.1 – Класифікація нелінійних рівнянь
Функція називається алгебраїчною, якщо для отримання значення
функції на заданої множині Х потрібно здійснити арифметичні операції та піднесення в степінь з раціональним або ірраціональним показником. Рівняння, які містять алгебраїчні функції називаються нелінійними алгебраїчними рівняннями.
До трансцендентних функцій відносять всі неалгебраїчні функції:
Показникові ах, логарифмічні ![]() ,
,![]() , тригонометричні sin x, cos x, tgx, ctgx, обернені тригонометричні
, тригонометричні sin x, cos x, tgx, ctgx, обернені тригонометричні ![]() та інші.
та інші.
Нелінійні рівняння, які містять трансцендентні функції називаються нелінійними трансцендентними рівняннями.
Розв’язком нелінійного рівняння на ЕОМ називається вектор ![]() , координати якого
, координати якого ![]() при підстановці в початкове рівняння перетворює його в тотожність.
при підстановці в початкове рівняння перетворює його в тотожність.
В нелінійному рівнянні виду
![]() (4.3)
(4.3)
і-та координата вектора ![]() називається і- тим коренем рівняння, а а1, а2, …, ат - коефіцієнтами рівняння (4.3).
називається і- тим коренем рівняння, а а1, а2, …, ат - коефіцієнтами рівняння (4.3).
Процес розв’язання нелінійних рівнянь вигляду (4.1) або (4.2) на ЕОМ розбивається на два етапи:
1. відокремлення коренів;
2. уточнення коренів.
Перший етап іноді можна виконувати вручну, другий же виконується за допомогою спеціальних методів уточнення коренів та програм. Розглянемо особливості етапу відокремлення коренів.
Корінь ![]() рівняння
рівняння ![]() , вважається відокремленим на відрізку
, вважається відокремленим на відрізку ![]() , якщо на цьому відрізку дане рівняння не має інших коренів.
, якщо на цьому відрізку дане рівняння не має інших коренів.
Відокремити корені – це означає розбити всю область допустимих значень ![]() (ОДЗ) на відрізки, в кожному з яких міститься один корінь (рис 4.2). Відокремлення коренів можна здійснити двома способами – графічним та аналітичним.
(ОДЗ) на відрізки, в кожному з яких міститься один корінь (рис 4.2). Відокремлення коренів можна здійснити двома способами – графічним та аналітичним.
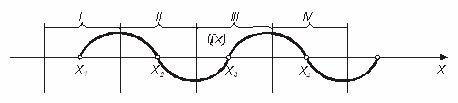
Графічний метод. Будують графік функції ![]() для рівняння виду
для рівняння виду ![]() або представляють рівняння у вигляді
або представляють рівняння у вигляді ![]() та будують графіки функцій
та будують графіки функцій ![]() та
та ![]() . Значення дійсних коренів рівняння є абсцисами точок перетину графіка функції
. Значення дійсних коренів рівняння є абсцисами точок перетину графіка функції ![]() з віссю
з віссю ![]() або абсцисами точок перетину графіків функцій
або абсцисами точок перетину графіків функцій ![]() та
та ![]() . Відрізки, в яких знаходиться тільки по одному кореню, легко знаходяться наближено.
. Відрізки, в яких знаходиться тільки по одному кореню, легко знаходяться наближено.
Приклад 4.1. Знайти наближено графічним способом корені рівняння ![]() .
.
Розв’язок. Перепишемо рівняння наступним чином: ![]() Функції в лівій і правій частині рівняння мають спільну область визначення: інтервал
Функції в лівій і правій частині рівняння мають спільну область визначення: інтервал ![]() . Тому будемо шукати корені саме на цьому інтервалі.
. Тому будемо шукати корені саме на цьому інтервалі.
Будуємо графіки функцій ![]() і
і ![]() (рис. 4.3).
(рис. 4.3).
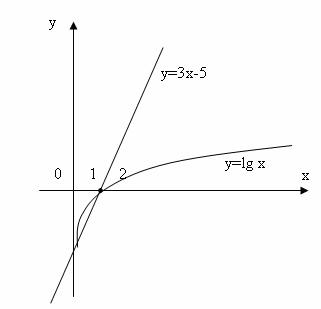
Пряма ![]() перетинає логарифмічну криву в двох точках з абсцисами х1
перетинає логарифмічну криву в двох точках з абсцисами х1![]() 0.00001 і х2
0.00001 і х2![]() 1.75. На рисунку 4.4 важко показати перетин графіків цих двох функцій в першій точці, але, враховуючи, що нижня вітка логарифмічної кривої необмежено прямує до осі Оу, можливо уявити, що перетин цих двох графіків пройде поблизу точки перетину графіка функції
1.75. На рисунку 4.4 важко показати перетин графіків цих двох функцій в першій точці, але, враховуючи, що нижня вітка логарифмічної кривої необмежено прямує до осі Оу, можливо уявити, що перетин цих двох графіків пройде поблизу точки перетину графіка функції ![]() і осі Оу. Абсциса точки перетину наближено дорівнює 0.00001. Отже корені рівняння х1
і осі Оу. Абсциса точки перетину наближено дорівнює 0.00001. Отже корені рівняння х1![]() 0.00001 і х2
0.00001 і х2![]() 1.75.
1.75.

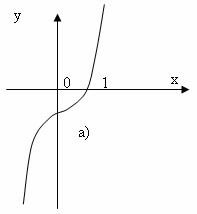
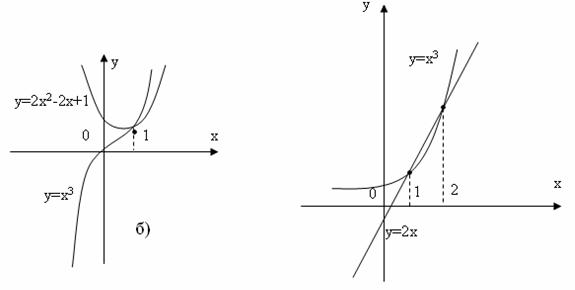
Приклад 4.2. Розв’язати графічно рівняння х3-2х2+2х-1=0.
Розв’язок. Перший спосіб: Побудуємо графік функції y=x3-2x2+2x-1 і визначимо абсциси точок перетину цього графіка з віссю Ох. Крива перетинає Ох в точці х=1, звідси витікає, що рівняння має один корінь (рис.4.5.а). (Відмітимо, що алгебраїчне рівняння третього степеня має один або три дійсних кореня. Так як крива перетинає вісь абсцис тільки в одній точці, то дане рівняння має тільки один дійсний корінь. Інші два кореня - комплексні.)
Другий спосіб: Представимо дане рівняння в вигляді х3=2х2-2х+1 і побудуємо графіки функцій y=х3 і y=2х2-2х+1. Знайдемо абсцису точки перетину цих графіків; отримаємо х=1 (рис.4.5.б), або область, де знаходиться точка перетину (тобто корінь рівняння).
Приклад 4.3. Знайти графічно корені рівняння ![]() .
.
Розв’язок. Будуємо графіки функцій ![]() та
та ![]() . Ці графіки перетинаються в двох точках, абсциси яких рівні. Дане рівняння має два кореня
. Ці графіки перетинаються в двох точках, абсциси яких рівні. Дане рівняння має два кореня ![]() та
та ![]() . (рис.4.6).
. (рис.4.6).
Аналітичний метод. Аналітично корні рівняння ![]() можна відокремити, використовуючи деякі властивості функцій та однією з розглянутих нижче теорем.
можна відокремити, використовуючи деякі властивості функцій та однією з розглянутих нижче теорем.
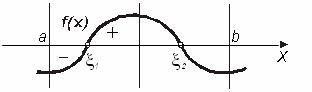
Теорема 1. Якщо функція ![]() неперервна на відрізку
неперервна на відрізку ![]() і приймає на кінцях цього відрізку значення різних знаків, то всередині відрізка
і приймає на кінцях цього відрізку значення різних знаків, то всередині відрізка ![]() існує хоча б один корінь рівняння
існує хоча б один корінь рівняння ![]() (рис.4.7).
(рис.4.7).
Теорема 2. Якщо функція ![]() неперервна та монотонна на відрізку
неперервна та монотонна на відрізку ![]() і приймає на кінцях відрізка значення різних знаків, то всередині відрізка
і приймає на кінцях відрізка значення різних знаків, то всередині відрізка ![]() існує корінь рівняння
існує корінь рівняння ![]() , і цей корінь єдиний (рис.4.8.а).
, і цей корінь єдиний (рис.4.8.а).
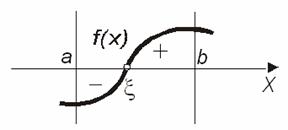
Теорема 3. Якщо функція ![]() неперервна на відрізку
неперервна на відрізку ![]() і приймає на кінцях цього відрізку значення різних знаків, а похідна
і приймає на кінцях цього відрізку значення різних знаків, а похідна ![]() зберігає постійний знак всередині відрізка, то всередині відрізка існує єдиний корінь рівняння
зберігає постійний знак всередині відрізка, то всередині відрізка існує єдиний корінь рівняння ![]() (рис.4.8.б).
(рис.4.8.б).
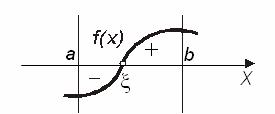
Для відокремлення коренів аналітичним методом можна рекомендувати наступний алгоритм:
1. Дослідити дане рівняння на монотонність і неперервність, визначити область допустимих та граничних значень.
2. Знайти ![]() – першу похідну, прирівняти її до нуля та знайти критичні точки.
– першу похідну, прирівняти її до нуля та знайти критичні точки.
3. Скласти таблицю знаків функції ![]() , використовуючи для
, використовуючи для ![]() значення критичних точок, граничних значень з ОДЗ і точок, отриманих на першому кроці при аналізі даного рівняння.
значення критичних точок, граничних значень з ОДЗ і точок, отриманих на першому кроці при аналізі даного рівняння.
4. Визначити інтервали, на кінцях яких функція приймає значення протилежних знаків. Всередині цих інтервалів існує по одному і тільки одному кореню.
Приклад 4.4. Відокремити корені рівняння x3+3x2-24x+1=0
Розв’язок.
1. ОДЗ рівняння (-![]() )
)
2. Визначимо першу похідну функції f(x): f'(x)=3x2+6x-24 та критичні точки, для чого f'(x)=0: x1=-4; x2=2
3. Складемо таблицю знаків виду
x |
- |
-4 |
2 |
+ |
Sign f(x) |
- |
+ |
- |
+ |
В результаті аналізу таблиці отримаємо три відрізка на яких функція змінює знак: (- ![]() ,-4], [-4,2], [2,
,-4], [-4,2], [2, ![]() ).
).
Розширимо таблицю, щоб отримати точні значення кінців відрізків
x |
- |
-7 |
-6 |
-5 |
-4 |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
+ |
Sign f(x) |
- |
- |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
- |
- |
- |
+ |
+ |
Аналіз таблиці дозволяє обрати три відрізка, на яких функція f(x) змінює знак.
4) Наступним етапом дослідження рівняння на ЕОМ є етап уточнення значення кореня з заданою ![]() на кожному відрізку.
на кожному відрізку.
Розглянемо суть другого етапу наближеного розв’язання нелінійних рівнянь – уточнення коренів, тобто доведення їх до заданого степеню точності. Для уточнення коренів нелінійного рівняння з заданою похибкою ![]() на деякому відрізку
на деякому відрізку ![]() на ЕОМ в інженерній практиці найбільш широко використовують:
на ЕОМ в інженерній практиці найбільш широко використовують:
Всі ці методи являються ітераційними, тобто побудовані на алгоритмах, в яких одна з їх частин повторюється багаторазово, при чому кількість повторень залежить від початкових даних (від задано( користувачем похибки, від відрізка дослідження та інше).
Розглянемо особливості цих методів та алгоритмів, на яких вони базуються.
Постановка задачі
Нехай маємо рівняння ![]() , де
, де ![]() – неперервна, монотонна нелінійна функція, яка має на відрізку
– неперервна, монотонна нелінійна функція, яка має на відрізку ![]() єдиний корінь
єдиний корінь ![]() , тобто добуток
, тобто добуток ![]() , причому
, причому ![]() , де
, де ![]() – задана похибка обчислень. Потрібно знайти значення кореня
– задана похибка обчислень. Потрібно знайти значення кореня ![]() з заданою похибкою
з заданою похибкою ![]() (рис. 4.9).
(рис. 4.9).
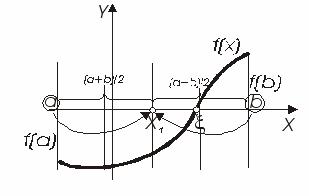
Алгоритм методу (рис.4.9) оснований на багатократному ділені навпіл і звужуванні досліджуваного відрізка ![]() , який отримали в результаті попереднього дослідження функції
, який отримали в результаті попереднього дослідження функції ![]() (відокремлення коренів).
(відокремлення коренів).
Метод половинного ділення – це найпростіший метод уточнення кореня рівняння. Він сходиться для будь-яких неперервних функцій ![]() , в тому числі недиференційованих. Швидкість сходження невелика
, в тому числі недиференційованих. Швидкість сходження невелика
![]() .
.
1. На відрізку ![]() вибираємо точку
вибираємо точку ![]() , яка розділяє його на два рівних відрізки
, яка розділяє його на два рівних відрізки ![]() і
і ![]() , довжина яких рівна і знаходиться за формулою
, довжина яких рівна і знаходиться за формулою
![]()
2. Перевіряємо чи ![]() , якщо так, то
, якщо так, то ![]() – точний корінь початкового рівняння і переходимо до пункту 6.
– точний корінь початкового рівняння і переходимо до пункту 6.
3. У випадку, коли ![]() , то з двох отриманих відрізків
, то з двох отриманих відрізків ![]() і
і ![]() вибираємо той, на кінцях якого функція
вибираємо той, на кінцях якого функція ![]() приймає значення протилежних знаків, тобто, якщо
приймає значення протилежних знаків, тобто, якщо ![]() , тоді залишаємо відрізок
, тоді залишаємо відрізок ![]() і точку
і точку ![]() переносимо в точку
переносимо в точку ![]() (
(![]() ); якщо
); якщо![]() , то залишаємо відрізок
, то залишаємо відрізок ![]() і переносимо точку
і переносимо точку ![]() в точку
в точку ![]() (
(![]() ) і переходимо до пункту 1.
) і переходимо до пункту 1.
4. Процес ділення відрізка навпіл виконується доти, поки на якомусь етапі, або середина відрізка буде коренем, або буде виконана умова закінчення ітераційного процесу: ![]() .
.
5. У цьому випадку за наближене значення кореня вибирають ![]() .
.
6. Вивід результатів. Кінець алгоритму.
7. Відомо, що при цьому похибка не перевищує ![]() , де
, де ![]() – число ітерацій.
– число ітерацій.
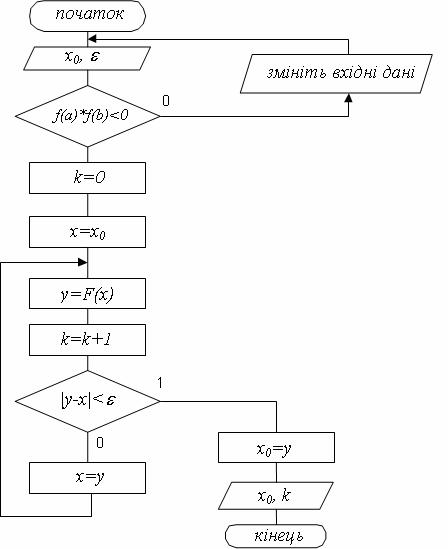
Схема алгоритму розв'язання нелінійного рівняння методом половинного ділення представлена на рисунку 4.10.
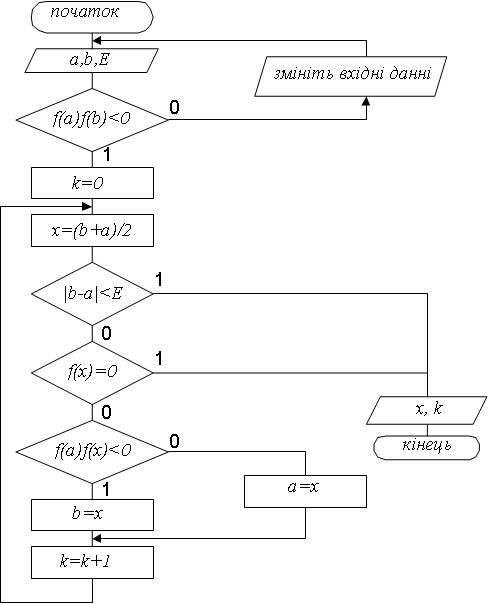
Метод хорд є одним з найбільш поширених методів розв’язання алгебраїчних і трансцендентних рівнянь. В літературі він також зустрічається під назвою "метод лінійного інтерполювання" і "метод пропорційних частин".
Постановка задачі
Розглянемо рівняння ![]() , де
, де ![]() неперервна нелінійна функція, яка на відрізку
неперервна нелінійна функція, яка на відрізку ![]() монотонна, диференційована і має єдиний корінь
монотонна, диференційована і має єдиний корінь ![]() (тобто
(тобто ![]() ). Потрібно знайти наближене значення кореня
). Потрібно знайти наближене значення кореня ![]() з заданою похибкою
з заданою похибкою ![]() .
.
Суть методу хорд полягає в тому, що на достатньо малому відрізку ![]() дуга функції
дуга функції ![]() замінюється хордою ab, яка її стягує. За наближене значення кореня приймається точка х1 перетину хорди з віссю
замінюється хордою ab, яка її стягує. За наближене значення кореня приймається точка х1 перетину хорди з віссю ![]() (рис.4.11.а).
(рис.4.11.а).
Рівняння хорди, яка проходить через точки має вигляд
![]() (4.4)
(4.4)
Знайдемо значення ![]() , для якого
, для якого ![]() , тобто для нерухомого кінця:
, тобто для нерухомого кінця:
![]() (4.5)
(4.5)
Ця формула називається формулою методу хорд. Тепер корінь ![]() знаходиться всередині відрізка
знаходиться всередині відрізка ![]() . Значення кореня
. Значення кореня ![]() можна уточнити за допомогою метода хорд на відрізку
можна уточнити за допомогою метода хорд на відрізку ![]() , тоді нове наближене значення кореня х2 знаходиться за формулою
, тоді нове наближене значення кореня х2 знаходиться за формулою
![]() .
.
Аналогічна для всякого ![]() -го наближення до точного значення кореня
-го наближення до точного значення кореня ![]() даного рівняння використовується формула:
даного рівняння використовується формула:
![]() (4.6)
(4.6)
Процес стягування хордою продовжується багаторазово доти, поки не одержано наближений корінь із заданим степенем точності
![]() (4.7)
(4.7)
де ![]() – наближені значення коренів рівняння
– наближені значення коренів рівняння ![]() , відповідно на
, відповідно на ![]() і
і ![]() -му ітераційному кроці;
-му ітераційному кроці; ![]() – задана точність обчислень.
– задана точність обчислень.
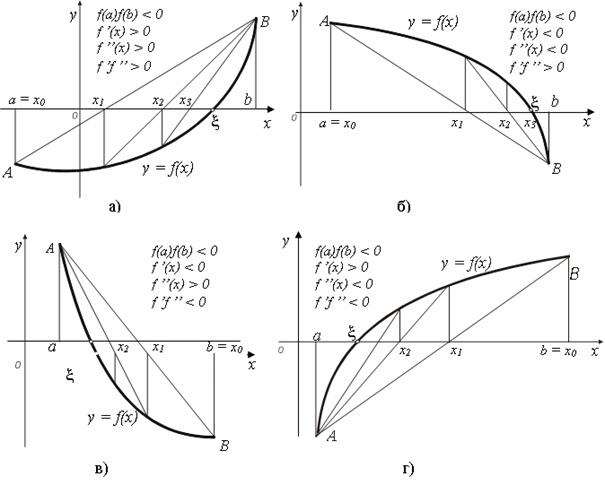
Слід відмітити, що розглянутий випадок (рис.4.11.а) перетину функції ![]() відрізку
відрізку ![]() не є єдиним. Існує ще три варіанти перетину функції, кожний з яких відрізняється напрямком побудови хорд і відповідно рухомими кінцями відрізку. Наприклад, на рис.4.11.а,б рухомий кінець відрізку а, а на рис.4.11.в,г рухомий кінець –
не є єдиним. Існує ще три варіанти перетину функції, кожний з яких відрізняється напрямком побудови хорд і відповідно рухомими кінцями відрізку. Наприклад, на рис.4.11.а,б рухомий кінець відрізку а, а на рис.4.11.в,г рухомий кінець – ![]() і відповідно формула 4.5 для нього має вигляд:
і відповідно формула 4.5 для нього має вигляд:
![]()
Для автоматизації цього алгоритму необхідно розробити правило для автоматичного вибору рухомого кінця хорди і відповідно формули для обчислення наближеного значення кореня. Існує два правила визначення рухомого кінця хорди.
Правило 1. Нерухомим кінцем відрізка є той, для якого знак функції співпадає із знаком другої похідної. Якщо ![]() , то нерухомим є кінець
, то нерухомим є кінець ![]() , а всі наближення до кореня
, а всі наближення до кореня ![]() лежать зі сторони кінця
лежать зі сторони кінця ![]() . Якщо
. Якщо ![]() , то нерухомим є кінець
, то нерухомим є кінець ![]() , а всі наближення до кореня
, а всі наближення до кореня ![]() лежать зі сторони кінця
лежать зі сторони кінця ![]() (рис.4.11.а,б,в,г).
(рис.4.11.а,б,в,г).
Правило 2. Якщо добуток першої на другу похідну функції ![]() більший за нуль:
більший за нуль: ![]() , то рухомий кінець
, то рухомий кінець ![]() ; якщо добуток першої на другу похідну менший за нуль:
; якщо добуток першої на другу похідну менший за нуль: ![]() , то рухомий кінець
, то рухомий кінець ![]() .Схема алгоритму розв'язання нелінійного рівняння методом хорд представлена на рисунку 4.12.
.Схема алгоритму розв'язання нелінійного рівняння методом хорд представлена на рисунку 4.12.
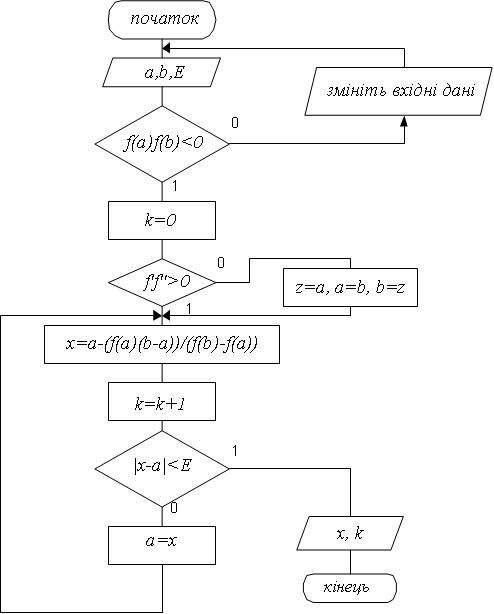
1. Метод половинного ділення та метод хорд розробляються як незалежні підпрограми-функції з вхідними параметрами: a, b, ![]() та вихідними: x, k, де x – наближене значення кореня, k– кількість ітерацій.
та вихідними: x, k, де x – наближене значення кореня, k– кількість ітерацій.
2. В цих підпрограмах-функціях необхідно передбачити перевірку вхідних даних, наприклад, чи дійсно відрізок вибраний так, що функція на його кінцях має різні знаки.
3. Обчислення перших та других похідних здійснюється за допомогою спеціальних функцій, в котрих заданий математичний вигляд похідної.
4. Перед викликом підпрограми-функції, реалізуючої метод необхідно аналітично визначити кількість коренів. Аналітично чи програмно відокремити корені і в циклі по кількості коренів викликати функцію, яка реалізує метод уточнення коренів так, щоб на екрані були виведені всі відрізки, корені на кожному з цих відрізків та кількість ітерацій, за яку був отриманий кожен корінь.
Метод послідовних наближень, розроблений Ньютоном, дуже широко використовується при побудові ітераційних алгоритмів. Його популярність обумовлена тим, що на відміну від двох попередніх методів замість інтерполяції по двом значенням функції в методі Ньютона здійснюється екстраполяція за допомогою дотичної до кривої в одній точці.
Постановка задачі
Нехай корінь рівняння f(x)=0 відокремлений на відрізку ![]() , на якому нелінійна функція f(x)монотонна і має різні знаки на кінцях відрізку, причому похідні
, на якому нелінійна функція f(x)монотонна і має різні знаки на кінцях відрізку, причому похідні ![]() та
та ![]() неперервні та зберігають постійні знаки на всьому відрізку
неперервні та зберігають постійні знаки на всьому відрізку ![]() . Потрібно знайти наближене значення кореня
. Потрібно знайти наближене значення кореня ![]() з заданою похибкою
з заданою похибкою ![]() .
.
Геометричний зміст метода Ньютона полягає в тому, що дуга кривої ![]() на відрізку
на відрізку ![]() замінюється дотичною до цієї кривої, а наближене значення кореня визначається як точка перетину дотичної з віссю Ох, проведеної з одного з кінців досліджуваного відрізку. Рівняння дотичної має вигляд:
замінюється дотичною до цієї кривої, а наближене значення кореня визначається як точка перетину дотичної з віссю Ох, проведеної з одного з кінців досліджуваного відрізку. Рівняння дотичної має вигляд:
![]() .
.
Перший випадок. Нехай f(a)<0, f(b)>0, fў(x)>0, f''(x)>0 (рис. 4.13, а) або f(a)>0, f(b)<0, f'(x)<0, f''(x)<0 (рис. 4.11, б). Проведемо дотичну до кривої ![]() в точці B0(v; f(b)) і знайдемо абсцису точки перетину дотичної з віссю
в точці B0(v; f(b)) і знайдемо абсцису точки перетину дотичної з віссю ![]() . Відомо, що рівняння дотичної в точці B0(b; f(b)) має вид: y-f(b)=f'(b) (x-b).
. Відомо, що рівняння дотичної в точці B0(b; f(b)) має вид: y-f(b)=f'(b) (x-b).
Припускаючи y=0, x=x1, отримаємо
![]() (4.8)
(4.8)
Тепер корінь рівняння знаходиться на відрізку [a, x1]. Застосовуючи знову метод Ньютона, проведемо дотичну до кривої в точці B1(x1; f(x1)) і отримаємо
![]() ,
,
і так далі (рис. 4.13).
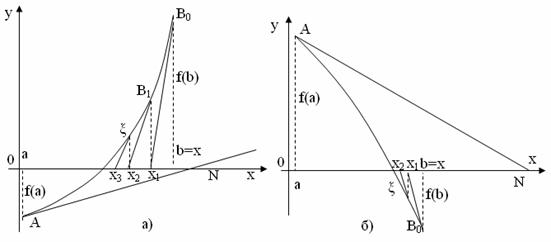
а) функція, яка досліджується, ввігнута (f'(x)>0, f''(x)>0)
б) функція, яка досліджується, опукла (f'(x)<0, f''(x)<0)
Даний процес ітераційний, тому формула для будь-якого n-го кроку ітерації має вигляд:
![]() . (4.9)
. (4.9)
В результаті отримана послідовність наближених значень x1, x2, ..., xn , ..., кожний наступний член якої ближчій до кореня ![]() , ніж попередній. Однак всі xn залишаються більше істинного кореня
, ніж попередній. Однак всі xn залишаються більше істинного кореня ![]() , тобто xn - наближене значення кореня
, тобто xn - наближене значення кореня ![]() з надлишком. Процес визначення кореня продовжується багаторазово доти, поки не одержано наближений корінь із заданим степенем точності
з надлишком. Процес визначення кореня продовжується багаторазово доти, поки не одержано наближений корінь із заданим степенем точності
Другий випадок. Нехай f(a)<0, f(b)>0, fў(x)>0, fўў(x)<0 (рис. 4.14, а) або f(a)>0, f(b)<0, f'(x)<0, f''(x)>0 (рис. 4.14).
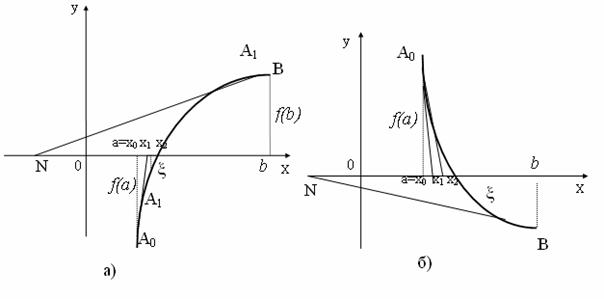
а) функція, яка досліджується, опукла (f'(x)>0, f''(x)<0)
б) функція, яка досліджується, ввігнута (f'(x)<0, f''(x)>0)
Якщо провести дотичну до кривої ![]() в точці B, то вона перетне вісь абсцис в точці, яка не належить відрізку
в точці B, то вона перетне вісь абсцис в точці, яка не належить відрізку ![]() . Тому проведемо дотичну в точці А0(a; f(a)) і запишемо її рівняння для даного випадку: y - f(a) = f'(a) (x - a).
. Тому проведемо дотичну в точці А0(a; f(a)) і запишемо її рівняння для даного випадку: y - f(a) = f'(a) (x - a).
Припускаючи, що y = 0, x = x1, отримаємо
![]() (4.10)
(4.10)
Корінь x знаходиться тепер на відрізку [x1, b]. Застосовуючи знову метод Ньютона, проведемо дотичну до кривої в точці A1(x1; f(x1)) і отримаємо
![]() ,
,
і загалом 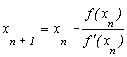 . (4.11)
. (4.11)
В результаті отримаємо послідовність наближених значень x1, x2,..., xn ,..., кожний наступний член якої ближчій до істинного кореня x, ніж попередній, т.б. xn - наближене значення кореня x з недостачею.
Порівнюючи формули (4.10), (4.11) з раніше виведеними, (а також враховуючи випадки, які розглядаються на рисунках 4.14а,б помічаємо, що вони відрізняються одна від одної тільки вибором початкового наближення: в першому випадку за x0 приймався кінець b відрізка, в другому - кінець а.
При виборі початкового наближення кореня необхідно використовувати наступне правило: за початкову точку слід вибирати той кінець відрізка [a, b], в якому знак функції співпадає зі знаком другої похідної. В першому випадку f(b)Чf''(x)>0 і початкова точка b=x0, в другому f(a)Ч f''(x)>0 і в якості початкового наближення беремо a=x0.
Для оцінки похибки можна користуватися загальною формулою
![]() , (4.12)
, (4.12)
де ![]() (ця формула підходить і до метода хорд).
(ця формула підходить і до метода хорд).
В тому випадку, коли відрізок ![]() настільки малий, що на ньому виконується умова М2<2m1 , де M2
настільки малий, що на ньому виконується умова М2<2m1 , де M2![]() , а
, а ![]() , точність наближення на n-му кроці інтерполяційного процесу оцінюється наступним чином: якщо
, точність наближення на n-му кроці інтерполяційного процесу оцінюється наступним чином: якщо 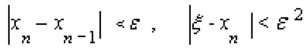 .
.
Якщо похідна f'(x) мало змінюється на відрізку ![]() , то для спрощення обчислень можна користуватися формулою
, то для спрощення обчислень можна користуватися формулою
![]() , (4.13)
, (4.13)
тобто значення похідної в початковій точці достатньо обчислити тільки один раз.
Процес побудови дотичної продовжується багаторазово доти, поки ![]() , де
, де ![]() – задана точність обчислень;
– задана точність обчислень; ![]() – наближені значення кореня рівняння
– наближені значення кореня рівняння ![]() , відповідно на
, відповідно на ![]() та і - тому ітераційному кроці. На рисунку 4.15 представлена схема алгоритму цього методу.
та і - тому ітераційному кроці. На рисунку 4.15 представлена схема алгоритму цього методу.
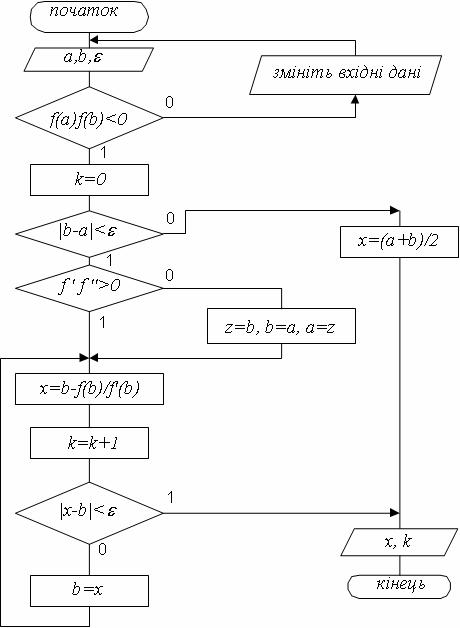
Правило 1. Якщо добуток першої на другу похідну функції ![]() більший за нуль:
більший за нуль: ![]() , то рухомий кінець
, то рухомий кінець ![]() ; якщо добуток першої на другу похідну менший за нуль:
; якщо добуток першої на другу похідну менший за нуль: ![]() , то рухомий кінець
, то рухомий кінець ![]() , тобто дотична будується в кінці
, тобто дотична будується в кінці ![]() .
.
Правило 2. Якщо знак функції на кінці відрізку співпадає зі знаком другої похідної, то цей кінець відрізка є рухомим, і в цій точці будується дотична.
Методи хорд і дотичних дають наближення кореня з різних сторін відрізку ![]() . Тому їх часто використовують в поєднанні один з одним, і процес уточнення кореня
. Тому їх часто використовують в поєднанні один з одним, і процес уточнення кореня ![]() нелінійного рівняння (4.1) проходить скоріше.
нелінійного рівняння (4.1) проходить скоріше.
Постановка задачі
Нехай дано рівняння (4.1)![]() , де
, де ![]() неперервна нелінійна функція, яка на відрізку
неперервна нелінійна функція, яка на відрізку ![]() монотонна, диференційована і має єдиний корінь
монотонна, диференційована і має єдиний корінь ![]() (тобто
(тобто ![]() ). Потрібно знайти наближене значення кореня
). Потрібно знайти наближене значення кореня ![]() з заданою похибкою
з заданою похибкою ![]() .
.
Використаємо комбінований метод хорд і дотичних з урахуванням поведінки функції на відрізку ![]() . Якщо f'(x)Чf''(x)>0, то метод хорд дає наближення кореня з недостачею, а метод дотичних – з залишком (рис.4.16.а,б). Якщо ж f'(x)Чf''(x)<0, то методом хорд отримуємо значення
. Якщо f'(x)Чf''(x)>0, то метод хорд дає наближення кореня з недостачею, а метод дотичних – з залишком (рис.4.16.а,б). Якщо ж f'(x)Чf''(x)<0, то методом хорд отримуємо значення
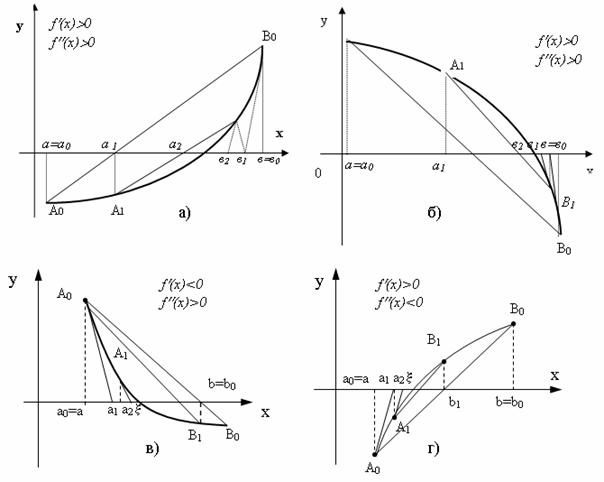
методом дотичних – з недостачею (рис.4.16.в,г). Однак в усіх випадках справжній корінь ![]() знаходиться між наближеними коренями, які отримані за методом хорд і методом дотичних, тобто виконується нерівність а< хn < x < хn<b, де хn – наближене значення кореня з недоліком,
знаходиться між наближеними коренями, які отримані за методом хорд і методом дотичних, тобто виконується нерівність а< хn < x < хn<b, де хn – наближене значення кореня з недоліком, ![]() `- з надлишком.
`- з надлишком.
Суть методу полягає в тому, що на досить малому відрізку ![]() (отриманому при відокремлені коренів) дуга функції
(отриманому при відокремлені коренів) дуга функції ![]() з одного кінця відрізка стягується хордою, а з другого – дотичною. Тобто, якщо сумістити обидва методи, то після знаходження коренів відрізок
з одного кінця відрізка стягується хордою, а з другого – дотичною. Тобто, якщо сумістити обидва методи, то після знаходження коренів відрізок ![]() на кожному кроці ітерації звужується шляхом переносу кінців відрізка
на кожному кроці ітерації звужується шляхом переносу кінців відрізка ![]() в точки перетину хорди та дотичної з віссю
в точки перетину хорди та дотичної з віссю ![]() .
.
Наближене значення кореня нелінійного рівняння визначається відповідно до таких правил:
Правило 1. Якщо добуток першої на другу похідну функції ![]() більший за нуль:
більший за нуль: ![]() , (рис. 4.16 а, б) то рухомим для методу хорд є кінець a, і наближене значення кореня з боку кінця a обчислюється за формулою хорд:
, (рис. 4.16 а, б) то рухомим для методу хорд є кінець a, і наближене значення кореня з боку кінця a обчислюється за формулою хорд:
![]() . (4.14)
. (4.14)
Для методу дотичних рухомим є кінець ![]() , і наближене значення кореня обчислюється за формулою дотичних:
, і наближене значення кореня обчислюється за формулою дотичних:
![]() . (4.15)
. (4.15)
Правило 2. Якщо добуток першої на другу похідну функції ![]() менший за нуль:
менший за нуль: ![]() (рис. 4.16 в, г), то рухомим для методу хорд є кінець b, і наближене значення кореня з боку кінця b обчислюється за формулою хорд:
(рис. 4.16 в, г), то рухомим для методу хорд є кінець b, і наближене значення кореня з боку кінця b обчислюється за формулою хорд:
![]() . (4.16)
. (4.16)
Для методу дотичних рухомим є кінець a, і наближене значення кореня обчислюється за формулою дотичних:
![]() . (4.17)
. (4.17)
Комбінований метод дуже зручний при оцінці похибки обчислень. Ітераційний процес продовжується доти, поки не стане виконуватися нерівність ![]() . За наближене значення кореня приймають
. За наближене значення кореня приймають ![]() , де
, де ![]() і
і ![]() – наближені значення кореня відповідно з недостачею та з надлишком.
– наближені значення кореня відповідно з недостачею та з надлишком.
Схема алгоритму методу представлено на рисунку 4.17.
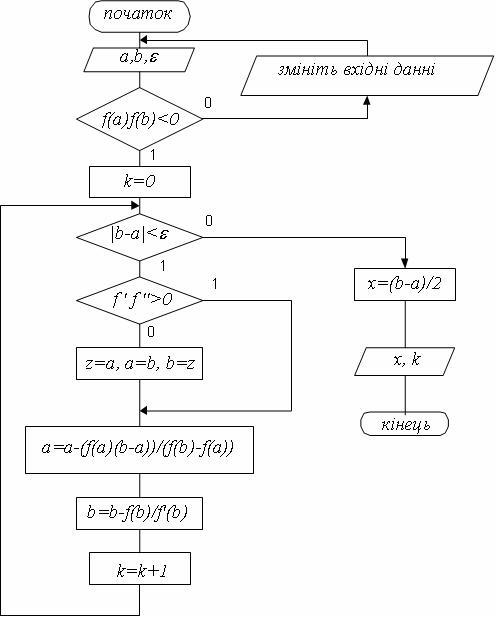
Суть методу полягає у заміні початкового рівняння
![]() (4.18)
(4.18)
еквівалентним йому рівнянням
![]() , (4.19)
, (4.19)
Постановка задачі
Нехай задано рівняння ![]() , де
, де ![]() – неперервна нелінійна функція. Потрібно визначити корінь
– неперервна нелінійна функція. Потрібно визначити корінь ![]() цього рівняння, який знаходиться на відрізку
цього рівняння, який знаходиться на відрізку ![]() з заданою похибкою
з заданою похибкою ![]() .
.
Виберемо довільним способом ![]() і підставимо його в праву частину рівняння (4.18); тоді отримаємо
і підставимо його в праву частину рівняння (4.18); тоді отримаємо ![]() . Потім це значення
. Потім це значення ![]() підставимо знову в праву частину рівняння (4.19) і отримаємо
підставимо знову в праву частину рівняння (4.19) і отримаємо ![]() (рис. 4.18 а,б). Повторюючи цей процес, отримаємо послідовність чисел
(рис. 4.18 а,б). Повторюючи цей процес, отримаємо послідовність чисел ![]() . При цьому можливі два випадки:
. При цьому можливі два випадки:
Приведемо без доказу теорему, яка виражає умову, при якій ітераційний процес розв’язку нелінійного рівняння методом ітерацій на ЕОМ збігається.
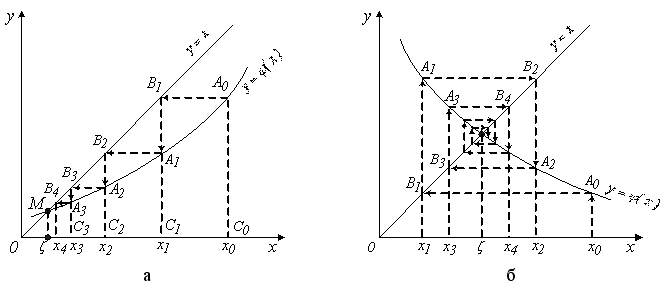
Теорема. Нехай на відрізку ![]() знаходиться єдиний корінь рівняння
знаходиться єдиний корінь рівняння ![]() та у всіх точках цього відрізку похідна
та у всіх точках цього відрізку похідна ![]() задовольняє нерівності
задовольняє нерівності ![]() . Якщо при цьому виконується і умова
. Якщо при цьому виконується і умова ![]() , то ітераційний процес збігається, а за нульове наближення
, то ітераційний процес збігається, а за нульове наближення ![]() можна взяти число з відрізку
можна взяти число з відрізку ![]() .
.
Розв’яжемо один етап ітерацій. Виходячи із заданого на попередньому кроці значення ![]() , обчислюємо
, обчислюємо ![]() . Якщо
. Якщо ![]() , покладемо
, покладемо ![]() і виконаємо наступну ітерацію. Якщо ж
і виконаємо наступну ітерацію. Якщо ж ![]() , то обчислення закінчують, за наближене значення кореня приймають величину
, то обчислення закінчують, за наближене значення кореня приймають величину ![]() .
.
При використанні методу простих ітерацій основною операцією є вибір функції ![]() в рівнянні
в рівнянні ![]() , яку слід підібрати так, щоб
, яку слід підібрати так, щоб ![]() і швидкість сходження послідовності
і швидкість сходження послідовності ![]() до кореня
до кореня ![]() тим вища, чим менше число
тим вища, чим менше число ![]() . Схема алгоритму метода ітерацій представлена на рисунку 4.19.
. Схема алгоритму метода ітерацій представлена на рисунку 4.19.
Таким чином, необхідна точність буде досягнута, якщо виконується нерівність |хn – xn - 1 | ![]() 0,00002. За нульове наближення можна прийняти будь-який із кінців відрізка (-0,725; -0,7) і будь-яку точку усередині нього. Нехай х0= -0,7. Обчислення зводимо в наступну таблицю:
0,00002. За нульове наближення можна прийняти будь-який із кінців відрізка (-0,725; -0,7) і будь-яку точку усередині нього. Нехай х0= -0,7. Обчислення зводимо в наступну таблицю:
Достатньо велика кількість інженерних задач на проміжному етапі вирішення зводиться до вирішення системи нелінійних рівнянь. Це одна з найважчих задач з точки зору реалізації її на ЕОМ. Одним із найбільш простих алгоритмів її рішення є метод Ньютона. Це найбільш розповсюджений метод розв’язання систем нелінійних рівнянь. Його популярність обумовлена тим, що в порівнянні з методом простої ітерації він забезпечує найбільш швидку збіжність. В основі методу Ньютона лежить представлення всіх n рівнянь у вигляді рядів Тейлора.
Розглянемо алгоритм методу Ньютона.
Нехай дана система нелінійних рівнянь виду
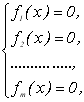 (4.20)
(4.20)
де ![]() – неперервно-диференційні функції.
– неперервно-диференційні функції.
2. Алгоритм методу базується на розкладі кожної функції системи в околі точки з координатами ![]() в ряд Тейлора.
в ряд Тейлора.
![]() члени рядів вищих порядків (
члени рядів вищих порядків (![]() тощо).
тощо).
1. Початкова система буде мати вигляд:
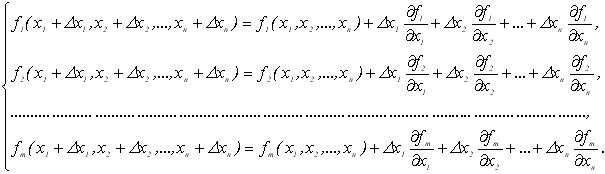 (4.21)
(4.21)
2. Припустимо, що прирости ![]() вибрані таким чином, що точки з координатами
вибрані таким чином, що точки з координатами ![]() є коренями даної системи рівнянь з заданим степенем наближення
є коренями даної системи рівнянь з заданим степенем наближення ![]() . Тоді ліву частину рівнянь системи (4.21) можна прирівняти до нуля, тобто система рівнянь (4.21) буде мати вигляд:
. Тоді ліву частину рівнянь системи (4.21) можна прирівняти до нуля, тобто система рівнянь (4.21) буде мати вигляд:
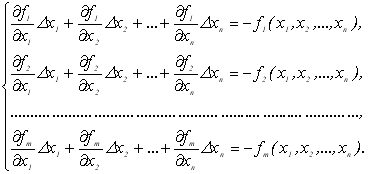 (4.22)
(4.22)
Або в матричній формі система (4.22) буде мати вигляд:
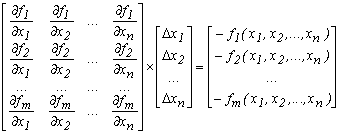 (4.23)
(4.23)
де 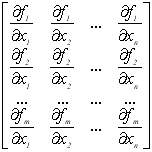 – матриця Якобі .
– матриця Якобі .
3. В результаті таких перетворень система рівнянь може розглядатися як система лінійних алгебраїчних рівнянь відносно ![]() . В такому випадку, якщо врахувати, що заданий вектор х початкових наближень виду:
. В такому випадку, якщо врахувати, що заданий вектор х початкових наближень виду:
![]() ,
,
можливо розв'язувати систему відносно вектора приросту ![]() , та знайти розв'язок системи, як сума попереднього значення та вектора
, та знайти розв'язок системи, як сума попереднього значення та вектора ![]() :
:
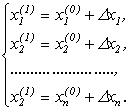 (4.24)
(4.24)
Дану задачу можна розв'язати з будь-якої точки, вибравши вектор початкових наближень.
4. Процес розв’язання системи нелінійних рівнянь (4.20) з використанням системи лінійних алгебраїчних рівнянь (4.23) відносно ![]() - ітераційний, та буде продовжуватись до тих пір, поки всі координати вектору приростів не стануть менше за абсолютною величиною заданої похибки
- ітераційний, та буде продовжуватись до тих пір, поки всі координати вектору приростів не стануть менше за абсолютною величиною заданої похибки ![]() , тобто
, тобто ![]() .
.
Схема алгоритму метода Ньютона представлена на рисунку 4.20.
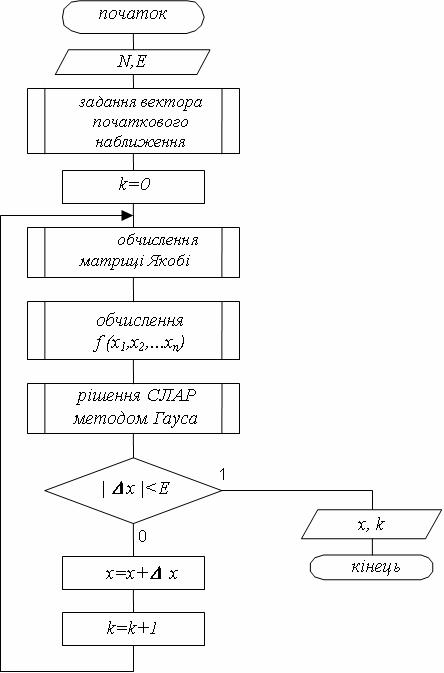
Приклад. Стійкість складної конструкції жорстких балок описується системою нелінійних рівнянь виду:
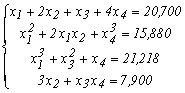
Розв’язати дану систему нелінійних рівнянь методом Ньютона.
Розв’язок. Для того, щоб розв’язати дану систему нелінійних рівнянь методом Ньютона необхідно перетворити систему до вигляду (4.23). Для цього знайдемо спочатку частині похідні всіх рівнянь системи в початкової точці для формування матриці Якобі, яка буде мати вигляд:
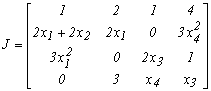
За допомогою програми, що складена відповідно алгоритму, який представлений на рисунку 4.20, для знаходження вектора розв’язку Х багаторазово методом Гауса розв’яжемо на ЕОМ систему виду:
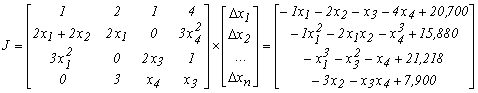
відносно вектору поправки ![]() з початковими значеннями змінних
з початковими значеннями змінних ![]() та з заданою похибкою
та з заданою похибкою ![]() , з яких починається ітераційний процес.
, з яких починається ітераційний процес.
В результаті можна отримати наступні результати:
Номер ітерації |
|
|
|
|
0 |
1.0000 |
1.0000 |
1.0000 |
1.0000 |
1 |
2,75037 |
4,6763 |
7,8958 |
0,1753 |
2 |
1,3448 |
5,2971 |
5,9494 |
0,7029 |
3 |
1,4775 |
3,8437 |
4,3419 |
1,7983 |
4 |
1,5427 |
6,2434 |
4,1204 |
0,6376 |
5 |
1,2364 |
5,7274 |
4,3436 |
0,9163 |
6 |
1,2024 |
5,5986 |
4,2995 |
1,0002 |
7 |
1,2000 |
5,6000 |
4,3000 |
1,0000 |
8 |
1,2000 |
5,6000 |
4,3000 |
1,0000 |
1. Щуп Т. Решение инженерных задач на ЕВМ. – М.: Мир, 1982. – 235с.
2. Демидович Б. П., Марон И. А. Основы вычислительной математики. – М.: Наука, 1970. – 664 с.
3. Демидович Б. П., Марон И. А., Шувалова Е. З. Численные методы анализа. – М.: Мир, 1967
4. Мак – Кракен Д., Дрон У. Численные методы и програмирование на фортране. – М.: Мир, 1977. – 584 с.
5. Бахвалов Н. С. Численные методы . Т. И. Анализ, алгебра, обычные диференциальные уравнения. – М.: Наука, 1975. – 631 с.
6. Краскевич В. Є., Зеленський К. Х., Гречко В. И. Численные методы в инженерных исследованиях. – К.: Высшая шк.., 1986. – 263 с.
7. Рисс Ф., Секефальви – Надь Б. Лекции по функциональному анализу – М.: Мир, 1979.
8. Плис А.И., Сливина Н.А. Mathcad. Математический практикум для инженеров и экономистов: – М.: Финансы и статистика, 2003. – 656с.
9. В.И. Бердышев, Ю.Н. Субботин. Численные методы приближения функций. – Средне-Уральское книжное книжное издательство, 1979.
10. Ортега Дж., Рейнболдт В. Итерационные методы решения нелинейных систем уравнений со многими неизвестными. – М.: Мир, 1975. – 558 с.
1. Які рівняння відносяться до нелінійних?
2. Які рівняння відносяться до трансцендентних?
3. Що є розв‘язком нелінійного рівняння?
4. Відокремити корені рівняння
![]() ,
, ![]()
5. Класифікація рівнянь, трансцендентні та алгебраїчні рівняння.
6. Які рівняння відносяться до трансцендентних рівнянь?
7. Які рівняння відносяться до алгебраїчних рівнянь?
8. Суть відокремлення коренів нелінійних рівнянь.
9. Суть методів уточнення коренів.
10. Які способи використовуються для відокремлення коренів?
11. В чому суть аналітичного методу відокремлення коренів?
12. Які теореми використовуються для аналітичного методу відокремлення коренів?
13. В чому суть алгоритму методу половинного ділення? Дайте геометричну інтерпретацію цього методу.
14. Графічна інтерпретація методу половинного ділення та основні формули методу.
15. В чому суть алгоритму методу хорд? Дайте геометричну інтерпретацію цього методу.
16. Графічна інтерпретація методу хорд та основні формули методу.
17. В чому суть алгоритму методу січних? Дайте геометричну інтерпретацію цього методу.
18. Графічна інтерпретація методу січних та основні формули методу.
19. В чому суть алгоритму комбінованого методу? Дайте геометричну інтерпретацію цього методу.
20. Графічна інтерпретація комбінованого методу та основні формули.
21. В чому суть алгоритму автоматизації пошуку рухомого кінця хорди?
22. В чому суть алгоритму автоматизації пошуку рухомого кінця січної?
23. Покажіть особливості методу ітерацій та його обмеження.
24. Графічна інтерпретація методу ітерацій та основні формули методу.
25. Розробить підпрограму - функцію для уточнення коренів нелінійного рівняння методом ітерацій.26.