Розглянемо особливості загального підходу до розв’язання СЛАР наближеними методами.

     3.2 Загальний підхід до розв’язання СЛАР наближеними методами

Розглянемо систему лінійних алгебраїчних рівнянь виду:

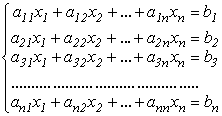                    (3.2)

Для розв’язання системи (3.2) методами послідовних наближень необхідно виконати наступні кроки:

1) Кожне рівняння системи розділити на діагональний елемент а_kk, де k=1,2...n, n – кількість рівнянь в системі, і перетворити кожне рівняння системи відносно координат вектора, індекс якого співпадає з номером рівняння:

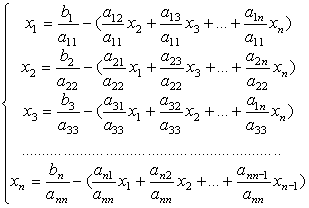          (3.3)

     2) Нехай , а , де k=1,2…n; i=1,2…n. Тоді система (3.3) матиме вигляд:

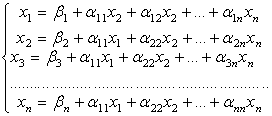               (3.4)

Така система називається зведеною до нормального вигляду.

     3) Представимо систему (3.4) в матричному вигляді:

,     (3.5)

або векторному

.                         (3.6)

Якщо деяким чином визначити, так званий, вектор початкових значень , який знаходиться в правій частині (3.6), то можна отримати певні значення вектора .

В якості вектора початкових наближень вибирають:

4) Якщо вектор початкових наближень підставити в праву частину системи (3.5) або (3.6), то вона прийме вигляд:

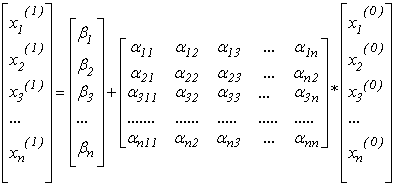
aбо ,

легко розв’язується, тому що в правої частині містить всі визначені елементи, і дозволяє отримати розв’язок системи, який називається вектором першого наближення .

5) Перевіряється виконання умови закінчення ітераційного процесу пошуку розв’язку системи (3.2) виду:

                         (3.7),

де - задана похибка результатів розв’язання задачі.

Якщо умова (3.7) не виконується, то підставляється в праву частину (3.5) або (3.6) і знаходиться з системи виду:

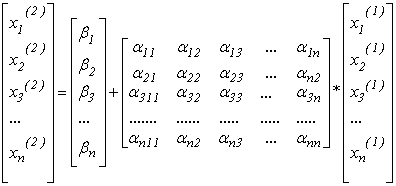
aбо .

6) Знову перевіряється виконання умови закінчення ітераційного процесу пошуку розв’язку системи (3.2)

.

Якщо умова не виконується, то підставляється в праву частину (3.5) і знаходиться з системи виду:

.

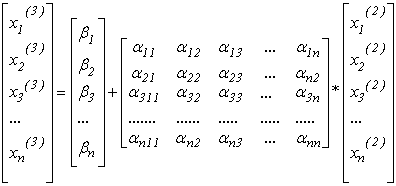і т.д.

7) Етапи 4 та 5 повторюються до тих пір поки на якому-небудь к - ому кроці не виконується умова

.                    (3.8)

Таким чином, процес пошуку розв’язку системи (3.2) наближеними методами з заданою похибкою є ітераційним, а умовою виходу з цього процесу є умова (3.8).

     3.3 Умови збіжності ітераційного процесу

Описаний вище алгоритм дозволяє отримати розв’язок системи (3.2) близький до точного (з заданою похибкою ) тільки в тому випадку, коли ітераційний процес пошуку розв’язку СЛАР збігається.

Теорема про збіжність. Ітераційний процес пошуку розв’язку системи лінійних алгебраїчних рівнянь виду (3.5) наближеними методами збігається, якщо будь-яка канонічна норма матриці .

Канонічною нормою матриці називається будь-яке дійсне додатне число, яке визначається за такими умовами:

перша канонічна норма – це максимальна з сум модулів елементів матриці коефіцієнтів по стрічкам:

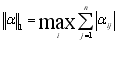,                    (3.9)

     друга канонічна норма – це максимальна з сум модулів елементів матриці коефіцієнтів по стовбцям:

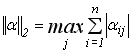,                    (3.10)

     третя канонічна норма – це корінь квадратний з сум квадратів модулів всіх елементів матриці коефіцієнтів :

.

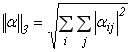Наслідок 1: Ітераційний процес розв’язання системи (3.4) збігається, якщо сума модулів елементів стрічок матриці коефіцієнтів або сума модулів елементів її стовбців менш одиниці, тобто виконується умова

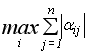<1     або умова  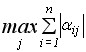    <1.     (3.11)

Наслідок 2: Ітераційний процес розв’язання системи (3.4) збігається, якщо елементи головної діагоналі більше суми модулів елементів відповідної стрічки крім діагонального елементу цієї стрічки, тобто виконується умова:

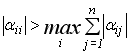     або умова  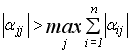   .     (3.12)

Приклад.

Визначити, чи збігається ітераційний процес для системи рівнянь

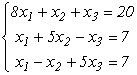або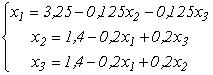

Матриця даної системи має вигляд:

Визначаємо норми:

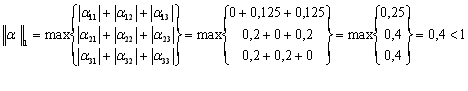
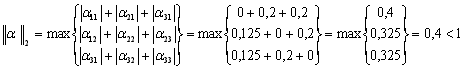
Таким чином, перша та друга канонічні норми менш одиниці, тобто ітераційний процес для даної системи збігається.

Розглянемо особливості алгоритмів наближених методів.

     3.4 Метод послідовних наближень (метод Якобі)

Нехай задана система лінійних алгебраїчних рівнянь виду (3.2). Метод послідовних наближень (метод Якобі) відноситься до ітераційних методів, тому потребує перетворити дану систему до нормального вигляду (3.5) та знайти канонічні норми матриці , для того щоб визначити умови збіжності ітераційного процесу (3.9) - (3.11) пошуку розв’язку системи с заданою похибкою відповідно теоремі про збіжність. Якщо жодна з умов (3.3) – (3.11) не виконується, то дану систему необхідно перетворити по певним правилам, та знову перевірити умови збіжності ітераційного процесу (3.9) – (3.11). Якщо жодна з умов знову не виконується, то метод послідовних наближень не має сенсу використовувати. Якщо хоча б одна з умов (3.9) – (3.11) виконується, то ітераційний процес пошуку розв’язку системи с заданою похибкою збігається і метод послідовних наближень можна використовувати.

По-перше, вибирається певне значення вектору початкових наближень , яке підставляється в праву частину системи рівнянь виду:

,     (3.13)

що легко розв’язується для знаходження вектора розв’язку першого наближення , тому що в правої частині містить всі визначені елементи.

По-друге, перевіряється виконання умови закінчення ітераційного процесу виду:

де - задана похибка результатів розв’язання задачі. Якщо умова не виконується, то підставляється в праву частину системи (3.5) і знаходиться :

та знову перевіряється виконання умови закінчення ітераційного процесу виду:

.

За аналогією будь-яке (К+1)-е наближення можна обчислити за формулою:

, де к=0,1,2.....               (3.14)

Якщо послідовність , що отримана в результаті ітераційного процесу, має границю , то ця границя є розв’язком системи. Умова закінчення ітераційного процесу має вигляд:

,                    (3.15)

де - задана похибка результатів розв’язання системи.

Алгоритмічно перевірка умови (3.15) представляє собою алгоритм пошуку максимального відхилення між координатами вектора і і порівняння його з заданою похибкою .

Алгоритм методу послідовних наближень зображено на рисунку 3.1

    

Оцінка похибки метода Якобі

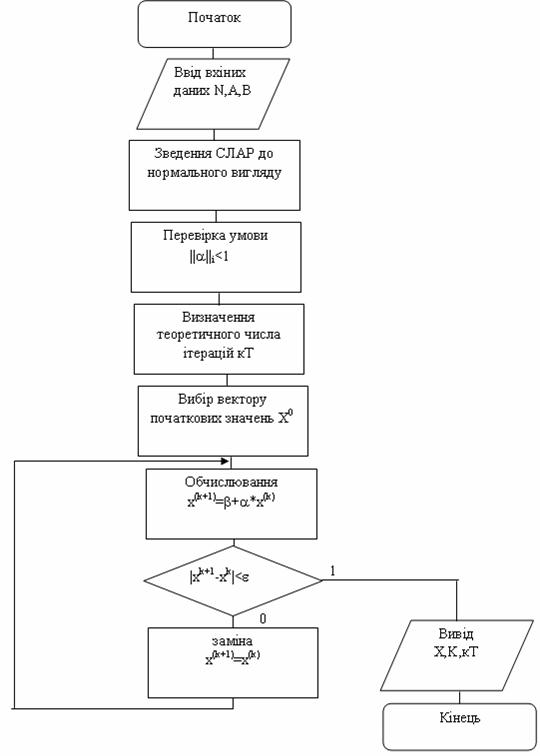
Якщо задана допустима похибка обчислень і x - вектор точного розв’язку системи лінійних рівнянь, а -те наближення до вектору точного розв’язку, то для оцінки похибки метода послідовних наближень використовується формула:

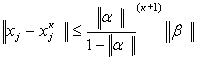,               (3.16)

де - одна з 3 норм матриці ; - аналогічна норма вектора ; - кількість ітерацій, необхідна для досягнення потрібної точності .

     3.5 Метод Гауса-Зейделя

Метод Зейделя являє собою модифікацію метода послідовних наближень, при чому у методі Зейделя при обчисленні і-ої координати вектора розв’язку - го наближення використовуються значення всіх (і-1) координат вектора - е наближення обчислені раніше. Розглянемо метод більш детально.

Нехай початкова система лінійних алгебраїчних рівнянь приведена до нормального вигляду:

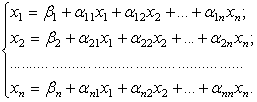               (3.17)

Алгоритм Гауса-Зейделя

Вибрати значення координат вектора початкових наближень

Визначити значення першої координати вектора першого наближення з першого рівняння системи:

Підставити в друге рівняння системи значення першої координати, яке обчислено на попередньому кроці

Отримані значення координат першого наближення , підставляємо у третє рівняння системи (3.14)

для знаходження третій координати і т.д.

1. Для знаходження останньої координати вектора першого наближення в останнє рівняння системи треба підставити значення всіх (n-1) координат (), які отримані на попередніх кроках та значення координати

6. Аналогічно будують друге, третє та інші наближення. Так для вектора (k+1) -го наближення за методом Зейделя використовуют наступні формули:

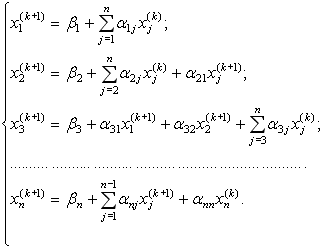          (3.18)

Умови збіжності ітераційного процесу Зейделя

Даний процес розв’язання СЛАР - ітераційний, тому важливим є аналіз умов збіжності ітераційного процесу. Процес Зейделя для системи лінійних рівнянь збігається до точного розв’язку с заданою похибкою при будь-якому виборі вектора початкових наближеннь, якщо будь яка норма матриці менша 1, тобто якщо:

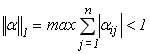                         (3.19)

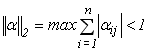                         (3.20)

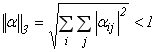                         (3.21)

Відомо, що процес Зейделя сходиться до точного розв’язку СЛАР швидше ніж метод послідовних наближень.

Приклад. Знайти першу та другу норми та проаналізувати умови збіжності ітераційного процесу для матриці , яка має вигляд :

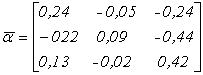
Очевидно, що процес ітерації для даної системи сходиться до точного розв’язку, не дивлячись на те, що

{0,59; 0,16; 1,1}=1,1>1.

Оцінка похибки методу Гауса-Зейделя

Якщо - точне значення вектора розв’язку системи лінійних рівнянь; а - к-е наближення, обчислене за методом      Гауса-Зейделя, то для оцінки похибки цього метода використовується формула:

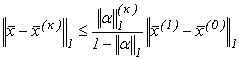               (3.22)

     3.6 Метод верхньої релаксації

В основі метода верхньої релаксації використовується алгоритм та обчислювальна схема метода Гауса-Зейделя, але на відміну від нього нові значення координат вектора к-го наближення визначаються за формулами:

,               (3.23)

де - уточнене значення змінної по методу Гауса-Зейделя, - параметр релаксації, значення якого визначається з інтервалу . При =1 метод тотожний методу Гауса-Зейделя. Швидкість збіжності ітераційного процесу залежить від значення .

     Література

1. Щуп Т. Решение инженерных задач на ЕВМ. – М.: Мир, 1982. – 235с.

2. Демидович Б. П., Марон И. А. Основы вычислительной математики. – М.: Наука, 1970. – 664 с.

3. Демидович Б. П., Марон И. А., Шувалова Е. З. Численные методы анализа. – М.: Мир, 1967Волков Е. А. Численные методы. – М.: Наука, 1988.

4. Мак – Кракен Д., Дрон У. Численные методы и програмирование на фортране. – М.: Мир, 1977. – 584 с.

5. Бахвалов Н. С. Численные методы . Т. И. Анализ, алгебра, обычные диференциальные уравнения. – М.: Наука, 1975. – 631 с.

     Питання та задачі до самостійної роботи

1. Дати визначення слідуючим термінам: розв’язання СЛАР, норма матриці, норма вектора, достатня умова сходження.

2. Дати порівняльну характеристику алгоритмів методу послідовного наближення та методу Гауса-Зейделя.

3. Суть алгоритму наближених методів розв’язання СЛАР.

4. Умова збіжності ітераційного процесу наближених методів.

5. Привести СЛАР:

9,9х1 -1,5х2+2,6х3=0;

0,4х₁+13,6х₂-4,2х₃=8,2;

0,7х₁+0,4х₂+7,1х₃=-13;

до нормального вигляду.

6. Записати достатню умову зближення ітераційного процесу.

7. Оцінка похибки метода послідовних наближень та метода Гауса-Зейделя.

8. Суть алгоритму метода послідовних наближень.

< Зміст >