Лекція № 2

     ЧИСЕЛЬНІ МЕТОДИ РОЗВ’ЯЗАННЯ СИСТЕМ ЛІНІЙНИХ АЛГЕБРАЇЧНИХ РІВНЯНЬ НА ЕОМ

 

Інженеру часто доводиться вирішувати алгебраїчні і трансцендентні рівняння і системи рівнянь, що можуть являти собою самостійну задачу (наприклад, аналіз рівноваги сил в жорсткій системі балок, або дослідження умов та параметрів рівноваги хімічної реакції, тощо) або частину більш складних задач. В обох випадках практична цінність чисельного методу в значній мірі визначається швидкістю і ефективністю отримання розв‘язку. Розглянемо найбільш відомі чисельні методи і ефективні алгоритми розв‘язання систем лінійних алгебраїчних рівнянь.

     2.1 Основні поняття та визначення

Системою лінійних алгебраїчних рівнянь (СЛАР) називають систему виду:

                    (2.1)

де     , () – невідомі; , () – вільні члени системи; , () – коефіцієнти системи.

В матричному вигляді рівняння (2.1) прийме вигляд:

,

де     ={} – вектор невідомих; ={} – вектор

вільних членів; ={} – матриця коефіцієнтів СЛАР.

Розв’язком системи лінійних алгебраїчних рівнянь (2.1) називають вектор , координати якого {} при підстановці у систему, що розв’язують, перетворюють кожне рівняння системи в тотожність .

Кількість невідомих m в системі називають порядком СЛАР. Систему лінійних алгебраїчних рівнянь називають сумісною, якщо вона має хоча б один ненульовий розв’язок. В протилежному випадку СЛАР називають несумісною. СЛАР називається визначеною, якщо вона має тільки один розв’язок (випадок, коли m=n). Систему називають невизначеною, якщо вона має безліч розв’язків (m№n). Система називається виродженою, якщо головний визначник системи дорівнює нулю. Система називається невиродженою, якщо головний визначник системи не дорівнює нулю.

Дві системи називаються еквівалентними, якщо ці системи сумісні, визначені і мають однаковий розв’язок.

СЛАР можна розв'язати на ЕОМ чисельними методами, якщо вона сумісна, визначена, невироджена.

     2.2 Класифікація методів розв’язання СЛАР на ЕОМ

Для розв’язання СЛАР на ЕОМ традиційно використовують дві групи чисельних методів, що представлені на рисунку 2.1:

     Рисунок 2.1. – Класифікація чисельних методів

  •  точні (метод Гауса, метод Гауса з вибором головного елементу, метод Гауса з одиничною матрицею, метод Гауса з перетвореною матрицею, метод Гауса-Халецького, метод Гауса-Жордана, метод Крамера);

  •  наближені (метод послідовних ітерацій, метод Гауса-Зейделя, метод векторів зміщень).

    До точних методів відносять методи, які дозволяють отримати точний розв’язок системи (2.1) за відповідну кількість операцій перетворення без урахування похибок заокруглення.

    До наближених методів відносять методи, які дозволяють отримати розв‘язок системи (2.1) у вигляді границі послідовності векторів , яка збігається до точного розв’язку системи, де:

         2.3 Особливості методів Гауса

    Найбільш відомим з точних методів розв’язання системи лінійних алгебраїчних рівнянь (2.1) є методи Гауса, суть яких полягає в тому, що система рівнянь, яка розв’язується, зводиться до еквівалентної системи з верхньою трикутною матрицею. Невідомі знаходяться послідовними підстановками, починаючи з останнього рівняння перетвореної системи. Алгоритми Гауса складаються із виконання однотипних операцій, які легко формалізуються. Однак, точність результату й витрачений на його отримання час у більшості випадків залежить від алгоритму формування трикутної матриці системи. У загальному випадку алгоритми Гауса складаються з двох етапів:

    Прямий хід, в результаті якого СЛАР (2.1), що розв‘язується, перетворюється в еквівалентну систему з верхньою трикутною матрицею коефіцієнтів виду:

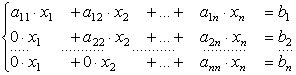                   (2.2)

    Зворотній хід дозволяє визначити вектор розв‘язку починаючи з останнього рівняння системи (2.2) шляхом підстановки координат вектора невідомих, отриманих на попередньому кроці.

    Відомо декілька різних алгоритмів отримання еквівалентної системи з верхньою трикутною матрицею. Розглянемо найбільш відомі з них.

         2.3.1 Метод Гауса з послідовним виключенням невідомих

    Метод Гауса з послідовним виключенням невідомих (базовий метод)засновано на алгоритмі, в основі якого лежить послідовне виключення невідомих вектора з усіх рівнянь, починаючи з (і+1)–го, шляхом елементарних перетворень: перемноження обох частин рівняння на будь-яке число, крім нуля; додавання (віднімання) до обох частин одного рівняння відповідних частин другого рівняння, помножених на будь-яке число, крім нуля.

    Суть алгоритму розглянемо на прикладі системи, яка складається з трьох лінійних алгебраїчних рівнянь з трьома невідомими:

                        (2.3)

    1) Перевіримо, щоб принаймні один із коефіцієнтів , , не дорівнював нулю. Якщо, наприклад, , тоді необхідно переставити рівняння так, щоб коефіцієнт при x1 у першому рівнянні не дорівнював нулю.

    2) Обчислюється множник:

    .                              (2.4)

    3) Перше рівняння системи (2.3) множиться на і віднімається від другого рівняння системи, отриманої після перестановки рівнянь, якщо вона була необхідною. Результат обчислення має вигляд:

    ,     (2.5)

    але 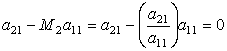. (2.6)

    Тоді виключається із другого рівняння.

    Позначимо нові коефіцієнти:

              (2.7)

    Тоді друге рівняння системи (2.3) набуває вигляду:

    .                    (2.8)

    Далі необхідно звільнитися від коефіцієнта при в третьому рівнянні системи (2.3) за аналогічним алгоритмом

    4) Обчислюється множник для третього рівняння:

    .                              (2.9)

    5) Перше рівняння системи (2.3) множиться на і віднімається від третього рівняння. Коефіцієнт при стає нулем, і третє рівняння набуває вигляду:

    ,                              (2.10)

    де ,                         (2.11)

    ,                              (2.12)

    .                              (2.13)

    Перетворена таким чином система рівнянь (2.3) набуває вигляду:

                   (2.14)

    Ця система рівнянь еквівалентна початковій і має певні переваги, оскільки входить тільки до першого рівняння. Спробуємо тепер виключити з останнього рівняння. Якщо , а , тоді переставимо друге й третє рівняння так, щоб . Інакше система вироджена і має безліч розв’язків.

    7) Обчислюємо множник .                    (2.15)

    8) Друге рівняння системи (2.11) помножується на М3ўў і віднімається від 3-го рівняння:

    .          (2.16)

    При цьому коефіцієнт біля дорівнює нулю:

    ,                         (2.17)

    ,                    (2.18)

    ,                         (2.19)

    Отримаємо           .               (2.20)

    Замінивши в системі (2.14) третє рівняння на (2.20), отримаємо систему рівнянь виду:

                   (2.21)

    Таку систему називають системою з трикутною матрицею коефіцієнтів, що еквівалентна СЛАР (2.3). Процес знаходження такої системи називається прямим ходом Гауса. Знайти розв’язок такої системи просто: із 3-го рівняння знайти , підставити результат у друге і знайти , підставити і в 1-е рівняння системи (2.21) і знайти за формулами:

    ,                              (2.22)

    ,                         (2.23)

    .                    (2.24)

    Процес знаходження вектора розв’язку системи (2.3) називають зворотнім ходом метода Гауса.

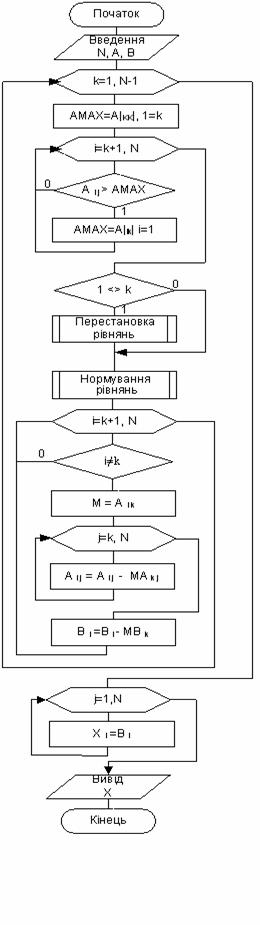
    На рисунку 2.2 показана схема алгоритму метода Гауса з послідовним виключенням для розв’язання системи із N рівнянь з N невідомими.

        
         Рисунок 2.2. – Схема алгоритму розв’язання системи лінійних алгебраїчних рівнянь методом Гауса.

    Ця схема відповідає розглянутому алгоритму і може бути використана при розробці програми. Блок “Перестановка рівнянь так, щоб ” означає деякий алгоритм, який дає змогу не допустити помилки “ділення на 0”. Якщо прямувати до можливого зменшення помилок округлення, то можна використати алгоритм з вибиранням головного елементу.

    Призначення індексів в схемі алгоритму (рисунок 2.2):

    к – номер рівняння, яке віднімається від інших, а також номер невідомого, яке виключається із залишених к-рівнянь;

    i – номер рівняння, із якого в даний момент виключається невідоме;

    j – номер стовпця.

         2.3.2 Метод Гауса за схемою Халецького

    Алгоритм метода включає також прямий і зворотній хід. Кінцевою метою прямого ходу є отримання СЛАР, яка еквівалентна заданій, з верхньою трикутною матрицею коефіцієнтів. Для цього матрицю коефіцієнтів початкової системи рівнянь А розбивають на дві трикутні:

    ,                         (2.25)

    де матриця С – нижня трикутна матриця; D – верхня трикутна матриця з одиничною головною діагоналлю:

    ; .

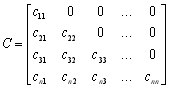    Алгоритм визначення коефіцієнтів матриць C i D.

    1) Обчислюється перший стовпець матриці С, перший рядок матриці D і за формулами:

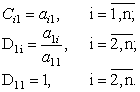                        (2.26)

                             (2.27)

    2) Обчислюються елементи другого стовпця матриці С:

    ,               (2.28)

    елементи другого рядка матриці D: , (2.29)

    і елемент :      .     (2.30)

    3) Обчислюють елементи третього стовпця матриці С:

                   (2.31)

    елементи третього рядка матриці D:

    ,                    (2.32)

    елемент у3

    ,                    (2.33)

    і т.д.

    Схема алгоритму метода Гауса за схемою Халецького показана на рисунку 2.3.

        
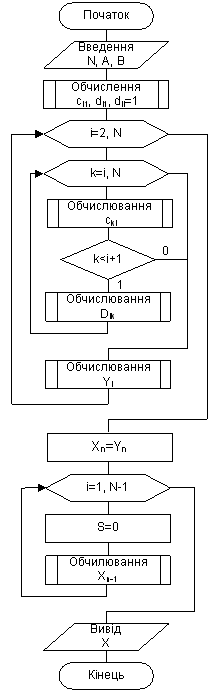
         Рисунок 2.3. – Схема алгоритму розв’язання лінійних алгебраїчних рівнянь методом Гауса за схемою Халецького

    Загальний вигляд формул для обчислення , , елементів матриць С, D i Y:

    ,               (2.34)

    ,                    (2.35)

    ,               (2.36)

    ,                         (2.37)

         2.3.3 Метод Гауса з вибором головного елемента

    Ідея цього методу виникла у зв’язку з тим, що коефіцієнти СЛАР є параметрами реальних інженерних систем та в більшості є наближеними значеннями, тому що отримані звичайно в результаті вимірювання або як статистичні дані. Для таких систем рівнянь при обчисленні масштабного множника

                                  (2.38)

    можлива ситуація при визначені , що ділення наближеного числа на достатньо мале число веде до різкого збільшення похибки методу. Тому для того, щоб не збільшувати похибку результату необхідно виконувати такі дії:

    1) в системі (2.1) необхідно знайти з k-го стовпця найбільший за абсолютним значенням коефіцієнт ak j ;

    2) переставити k-те рівняння з рівнянням у якому знаходиться цій максимальний коефіцієнт;

    3) масштабний множник буде обчислюватись за формулою (2.38), де  – максимальний коефіцієнт, а тому похибка розв’язання СЛАР у результаті арифметичних операцій не збільшується.

    Схема алгоритму метода Гауса з вибором головного елемента (прямий та обернений хід) показана на рисунку 2.4.

        
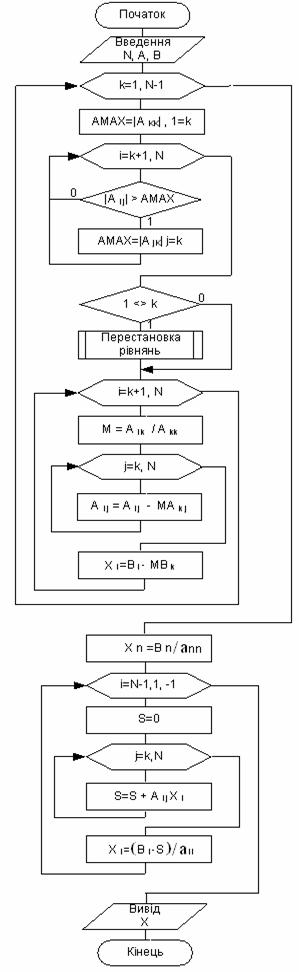
         Рисунок 2.4. – Схема алгоритму метода Гауса з вибором головного елемента
     

         2.3.4 Метод Гауса з одиничними коефіцієнтами

    В цьому методі зроблена спроба зменшити недоліки перших двох методів пов’язаних з багаторазовим діленням одного наближеного числа на інше. Для цього перед введенням масштабного множника k-те рівняння системи ділиться один раз на діагональний елемент так, щоб коефіцієнт при , а масштабний множник Мі буде дорівнювати ak j. Результатом прямого ходу є система, еквівалентна СЛАР (2.1), з одиничними коефіцієнтами на головній діагоналі виду:

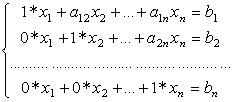                   (2.39)

    Дана система схожа на систему (2.2), яка отримується в результаті прямого ходу базового методу Гауса з послідовним вилученням невідомих і відрізняється від неї тільки діагональними коефіцієнтами. Для отримання такої системи необхідно використовувати алгоритм, який включає в себе наступні етапи:

    1. Організація циклу по всім рівнянням від 1 до N-1 (k = 1, 2, …, N-1).

    2. В кожному k-му стовпці визначається номер l-го рівняння з головним елементом (тобто номер l-го рівняння, в якому знаходиться коефіцієнт при зі всіх рівнянь починаючи з k-го до N-го).

    3. Якщо номер цього рівняння l не дорівнює k (l<>k), тоді необхідно переставити місцями l-е рівняння з k-м.

    4. Нормування k-го рівняння, тобто ділення всіх коефіцієнтів k-го рівняння на (головний елемент при ), включаючи .

    5. Перетворення всіх і-х рівнянь, починаючи з (k+1) до N у відповідності з базовим алгоритмом Гауса з метою отримати еквівалентну систему з верхньою трикутною матрицею коефіцієнтів.

    6. Кінець циклу по k.

    Формула зворотного ходу для систем виду (2.39) спрощується і має вигляд:

                        (2.40)

    Схема алгоритму методу Гауса з одиничними діагональними коефіцієнтами наведена на рисунку 2.5.

        
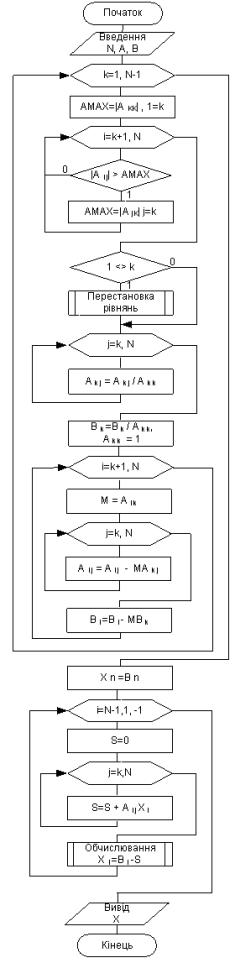
         Рисунок 2.5. – Схема алгоритму метода Гауса з одиничними коефіцієнтами
     

         2.3.5 Метод Гауса-Жордана

    Особливістю метода Гауса-Жордана є перетворення системи (2.1) (прямий хід) до еквівалентної з одиничною матрицею коефіцієнтів виду:

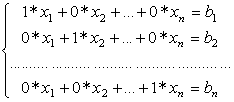         ,          (2.41)

    тобто системи, яка містить тільки одиничну діагональ.

    Для отримання такої системи в прямий хід алгоритму базового методу Гауса (з послідовним виключенням невідомих) додатково вводяться такі дії:

    1. Організація циклу по k по всім рівнянням від 1 до N -1 (k = 1, 2, …, N-1).

    2. Процедура вибору головного елементу в кожному k-му стовпці при ;

    3. Процедура нормування k-го рівняння системи, тобто в k-му рівнянні кожен коефіцієнт ak j розділити на , включаючи , так, щоб коефіцієнт =1.

    4. Перетворення всіх рівнянь системи, починаючи з 1-го до N у відповідності з базовим алгоритмом Гауса з метою отримати еквівалентну систему з одиничною діагоналлю. В даному випадку для розрахунку коефіцієнтів ai j використовуються ті самі формули, що і в базовому алгоритмі Гауса:

    ; ; ,

    але використовуються вони для всіх рівнянь з 1-го до N крім k-го, в якому остається коефіцієнт рівний одиниці.

    5. Кінець циклу по k.

    Обернений хід методу Гауса-Жордана дуже простий і використовує наступні формули:

    x k=b k , при k=1,2,…,n.

    Схема алгоритму методу Гауса-Жордана представлена на рисунку 2.6.

        
         Рисунок 2.6. – Схема алгоритму методу Гауса-Жордана

         Література

    1. Щуп Т. Решение инженерных задач на ЕВМ. – М.: Мир, 1982. – 235с.

    2. Демидович Б. П., Марон И. А. Основы вычислительной математики. – М.: Наука, 1970. – 664 с.

    3. Демидович Б. П., Марон И. А., Шувалова Е. З. Численные методы анализа. – М.: Мир, 1967Волков Е. А. Численные методы. – М.: Наука, 1988.

    4. Мак – Кракен Д., Дрон У. Численные методы и програмирование на фортране. – М.: Мир, 1977. – 584 с.

    5. Бахвалов Н. С. Численные методы . Т. И. Анализ, алгебра, обычные диференциальные уравнения. – М.: Наука, 1975. – 631 с.

         Питання та задачі до самостійної роботи

    1. Яку систему називають системою лінійних алгебраїчних рівнянь?

    2. Що називається розв'язком СЛАР?

    3. Яка система називається сумісною і несумісною?

    4. Яка система називається визначеною і невизначеною?

    5. Яка система називається виродженою і невиродженою?

    6. Які системи називаються еквівалентними?

    7. Яку СЛАР можна розв'язати на ЕОМ?

    8. Які методи відносять до точних (дати означення і перелічити методи)?

    9. Які методи відносять до наближених (дати означення і перелічити методи)?

    10. В чому суть алгоритмів методу Гауса?

    11. В чому суть прямого ходу в методах Гауса?

    12. В чому суть зворотного ходу в методах Гауса?

    13. Для чого в методі Гауса з послідовним виключенням елементів вводиться множник М і переставляють рівняння.

    14. Чим відрізняються алгоритми методів Гауса з послідовним виключенням елементів і вибором головного елементу?

    15. Чим відрізняються алгоритми методів Гауса з вибором головного елементу і з одиничною діагоналлю?

    16. Чим відрізняються алгоритми методів Гауса з одиничною діагоналлю і Гауса-Жордана?

    17. В чому суть методу Гауса за схемою Халецького?

    18. Яку систему отримано в результаті прямого ходу методу Гауса-Жордана?

    < Зміст >