Процес оптимізації лежить в основі всієї інженерної діяльності, оскільки класичні функції інженера полягають у тому, щоб, з одного боку, проектувати нові, ефективніші та менш дорогі технічні системи, а з другого - розробляти методи підвищення якості функціонування існуючих систем. Ефективність методів оптимізації, які дозволяють вибирати найкращий варіант без перевірки всіх можливих варіантів, тісно пов'язана із широким використанням досягнень у галузі математики шляхом реалізації ітераційних обчислювальних схем, що опираються на досить обґрунтовані методи та алгоритми із застосуванням обчислювальної техніки.
В даний час, в зв’язку з доступністю персональних комп’ютерів, велика увага приділяється використанню чисельних методів оптимізації в інженерній практиці, які можливо розділити на дві великі групи: методи безумовної і умовної оптимізації. Цей розподіл пов’язаний з різним описом простору проектування. Область дослідження, тобто область, в якій інженер намагається визначити оптимум певної задачі, називають простором проектування.
Простір проектування, який визначається проектними параметрами, зазвичай обмежений низкою умов, пов’язаних з фізичною сутністю задачі і розглядається в у вигляді двох варіантів:
1) якщо проектний параметр один, то зазвичай обмеження пов’язані з його значеннями, тобто область проектування звужується до відрізку дослідження [а, b];
2) якщо проектних параметрів декілька, то обмеження можуть накладатись або на їх значення, обмежуючи область дослідження, або в вигляді взаємозалежності між проектними параметрами, які повинні враховуватись при пошуку рішення (ці залежності в реальних задачах можуть відображати закони природи, економіки, права, наявність необхідних матеріалів і т. ін.).
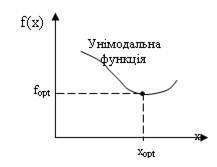
В даному розділі розглядаються методи безумовного одновимірного пошуку оптимуму цільової функції, які базуються на використанні першого варіанту представлення простору проектування, де цільова функція – це вираз (функція), значення якого інженер намагається мінімізувати або максимізувати. При цьому передбачається, що цільові функції, які досліджуються є унімодальними, тобто мають на інтервалі дослідження, який розглядається тільки один оптимум (рис. 13.1). Таке обмеження на характер цільової функції не є таким жорстким, як може здатися, так як багато задач, з якими інженер стикається в своїй практиці, виявляються унімодальними.
Чисельні методи, які орієнтуються на розв’язання задач безумовної оптимізації, можна розділити на три класи:
- методи прямого пошуку, що базуються на обчисленні тільки значень цільової функції;

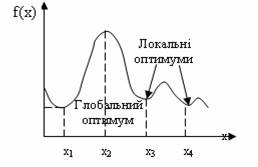
- градієнтні методи, в яких використовуються точні значення перших похідних f(х) ;
- методи другого порядку, в яких поряд з першими похідними використовуються також другі похідні функції f(x).
Задача одновимірної оптимізації ставиться таким чином: значення параметра Х цільової функції f(x), який називають проектним параметром, знаходяться на інтервалі дослідження [a, b]. В процесі пошуку оптимуму цільової функції цей інтервал, який називається інтервалом невизначеності, постійно зменшується (звужується), тому методи одновимірної оптимізації іноді називають методами звуження інтервалу невизначеності.
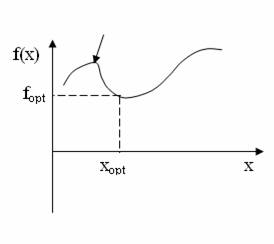
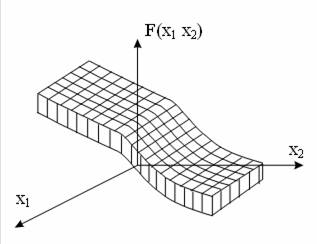
Вибір чисельного методу в першу чергу залежить від виду цільової функції, яка може бути однопараметричною і багатопараметричною (рис. 13.3, 13.4).
Деякі алгоритми оптимізації пристосовані до пошуку максимума, а інші – для пошуку мінімуму.
Однак, незалежно від типу задачі, яка розв’язується на екстремум (оптимум) можливо користуватись одним і тим же алгоритмом, так як задачу мінімізації можливо легко переробити в задачу на пошук мінімуму, змінивши знак цільової функції на протилежний (рис. 13.5).
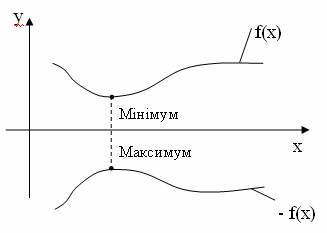
Загальна постановка задачі для методів одновимірної оптимізації ставиться наступним чином: нехай значення параметра Х знаходиться нa відрізку [a,b], а цільова функція унімодальнa в області, яку досліджуємо. Більшість чисельних методів одновимірної оптимізації - це методи звуження відрізка, а саме: метод розділення відрізку навпіл, метод дихотомії, метод золотого перерізу, метод Фібоначчі.
В процесі одновимірної оптимізації цільової функції на ЕОМ можна виділити два етапи:
1) встановлення меж відрізка, на якому реалізується процедура пошуку оптимуму;
2) зменшення відрізка до заданої похибки обчислення ![]() .
.
Перший етап реалізується за допомогою евристичних методів пошуку і є дуже складним. Другий - називають правилом виключення відрізків, реалізують алгоритм пошуку, що дозволяє знайти точку оптимуму шляхом послідовного виключення частин початкового обмеженого відрізка [a, b], тобто за допомогою ітераційних алгоритмів. В якості умови закінчення ітераційного процесу використовується момент, коли підінтервал, що залишився, зменшиться до достатньо малих розмірів (зазвичай для цього задають значення заданої похибки обчислення ![]() ).
).
Очевидно, найбільш природнім способом звуження інтервалу невизначеності для одновимірної унімодальної функції є ділення його на декілька рівних частин з наступним обчисленням значень цільової функції в вузлах отриманої сітки (рис. 13.6).
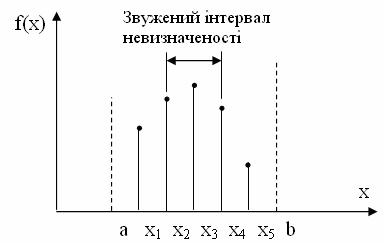
В результаті інтервал невизначеності звужується до двох кроків сітки. Звичайно говорять про дроблення інтервалу невизначеності, яке характеризується коефіцієнтом f. Розділивши інтервал невизначеності на N частин, отримаємо N+1 вузол, і тоді
![]() .
.
Щоб отримати значення f = 0,01, необхідно обчислити цільову функцію в 199 точках, а при f = 0,001 N=1999. Звідси видно, що ефективність цього методу при зменшенні інтервалу невизначеності швидко падає. Напрошується інший варіант: щоб отримати f=0,01, необхідно обчислити спочатку функцію в 19 точках і отримати f = 0,1, а потім обчислити ще 19 значень функції на скороченому інтервалі невизначеності, отримати f = 0,01, зробивши при цьому всього 38, а не 199 обчислень. Таким чином, при деякій винахідливості ефективність пошуку можна різко збільшити.
Суть метода полягає в постійному діленні відрізка дослідження цільової функції [a, b] навпіл і визначенні на ньому координат трьох точок х1, х2, хm. При чому значення їх визначаються як:
![]() , L=b-a,
, L=b-a, ![]() ,
, ![]() .
.
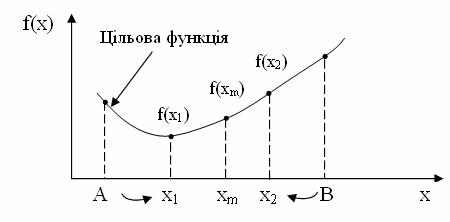
Точки ![]() , поділяють відрізок [a,b] на чотири рівні частини (рис. 13.6), обчислюємо значення цільової функції
, поділяють відрізок [a,b] на чотири рівні частини (рис. 13.6), обчислюємо значення цільової функції ![]() Потім порівнюємо значення
Потім порівнюємо значення ![]() і
і ![]() , якщо
, якщо ![]() , то виключаємо з дослідження відрізок
, то виключаємо з дослідження відрізок ![]() та покладемо
та покладемо ![]() . Тоді середньою точкою нового відрізка [a, b] стає
. Тоді середньою точкою нового відрізка [a, b] стає ![]() . Але якщо
. Але якщо ![]() , то порівнюємо значення цільової функції
, то порівнюємо значення цільової функції ![]() і
і ![]() ; якщо
; якщо ![]() , то виключаємо відрізок
, то виключаємо відрізок ![]() , покладемо
, покладемо ![]() ; якщо
; якщо ![]() , то виключаємо відрізок
, то виключаємо відрізок ![]() та
та ![]() , покладемо
, покладемо ![]() , тобто формуємо новий відрізок дослідження. Обчислюємо L = b - a, якщо
, тобто формуємо новий відрізок дослідження. Обчислюємо L = b - a, якщо ![]() , якщо немає, то знову повертаємося до початку.
, якщо немає, то знову повертаємося до початку.
Даний алгоритм ітераційний, тому зазвичай в якості умови закінчення ітераційного процесу обирають умову ![]() , тобто звуження відрізку виконується до тих пір, поки його величина не зменшиться до заданої обчислювальної похибки
, тобто звуження відрізку виконується до тих пір, поки його величина не зменшиться до заданої обчислювальної похибки ![]() . Алгоритм методу представлений на рис. 13.8.
. Алгоритм методу представлений на рис. 13.8.
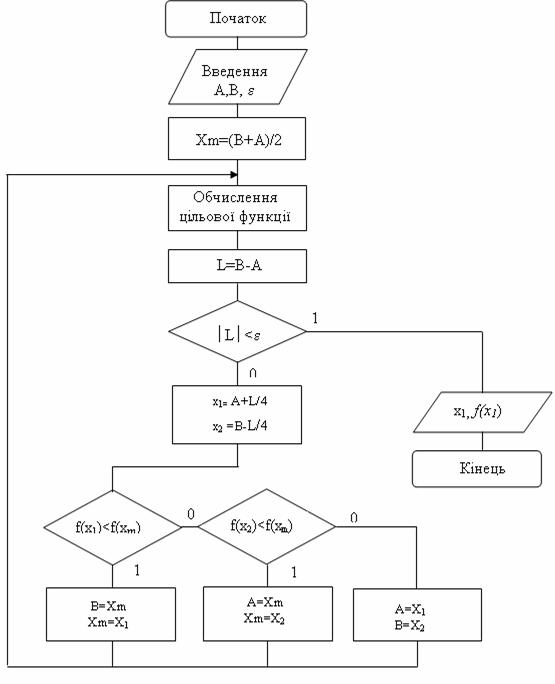
Цей метод відрізняється великою ефективністю.
Обчислення цільової функції в двох точках інтервалу невизначеності дозволяє його звузити. Можна таким чином обрати ці точки, що інтервал невизначеності буде мінімальним. На рис. 13.9 показані позначення, які використовуються в цій схемі.
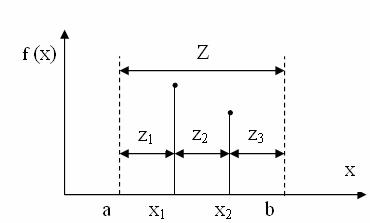
Якщо значення цільової функції при х1 більше, ніж при х2, то новий інтервал невизначеності дорівнює Z1 = z1 + z2. В протилежному випадку він визначається виразом Z2 = z2 + z3. Задача полягає в тому, щоб одночасно мінімізувати Z1 i Z2, задовольнивши умовам
z1+z2+z3 = Z,
z1 > 0,
z2 > 0,
z3 > 0.
Із рівності можна виключити z2. Тоді
Z – z3 = min, Z – z1 = min.
Так як величина Z задана, то праві частини цих рівнянь будуть тим менше, чим більше z1 i z3. Отже, оптимум відповідає умові
z1 = z3 = 0,5Z.
Але тоді z2 = 0, що суперечить умові z2 > 0.
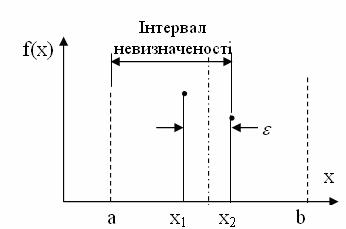
Нехай z2 має деяке дуже маленьке значення ![]() . Тоді із z1 i z3 віднімемо по
. Тоді із z1 i z3 віднімемо по ![]() . В результаті після обчислення першої пари значень цільової функції при близьких значеннях х інтервал невизначеності звузиться, як показано на рис. 13.10, і коефіцієнт ділення буде дорівнювати
. В результаті після обчислення першої пари значень цільової функції при близьких значеннях х інтервал невизначеності звузиться, як показано на рис. 13.10, і коефіцієнт ділення буде дорівнювати
![]() .
.
В межах, при ![]() ,
, ![]() . Надалі при використанні метода дихотомії виконуються ті операції, що і при використанні методу ділення відрізка навпіл.
. Надалі при використанні метода дихотомії виконуються ті операції, що і при використанні методу ділення відрізка навпіл.
З кожних трьох значень цільової функції, які були обчислені в інтервалі невизначеності в подальшому використовуються лише два, а третє не дає додаткової інформації і в подальшому не використовується. В методі золотого перетину цільова функція обчислюється в точках інтервалу невизначеності, які розташовані таким чином, щоб кожне обчислене значення цільової функції давало нову корисну інформацію.
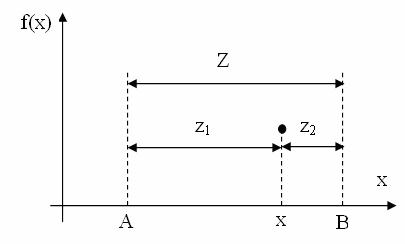
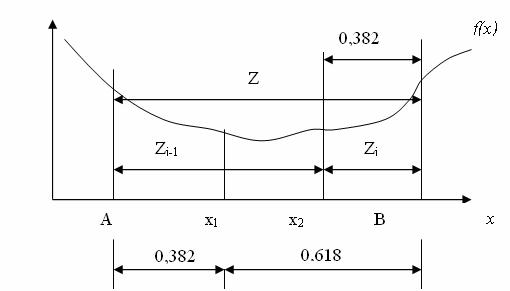
Суть цього методу полягає в наступному. Інтервал невизначеності ділиться на дві нерівні частини, відношення довжини більшого відрізку до довжини всього інтервалу дорівнює відношенню довжини меншого відрізку до довжини більшого відрізку. На рис. 13.11 показаний інтервал невизначеності Z, який складається з відрізків z1 i z2, відношення довжин яких визначається правилом золотого перетину.
![]()
Крім того, z1 + z2 = Z. Із першого рівняння витікає ![]() . Підставивши значення Z з другого рівняння і поділивши обидві частини на
. Підставивши значення Z з другого рівняння і поділивши обидві частини на ![]() , отримаємо
, отримаємо
![]()
Розв’язуючи це квадратне рівняння, знаходимо для додатнього кореня значення
![]()
На рис. 13.12 показано ділення інтервалу невизначеності в цьому відношенні і нанесені відповідні значення цільової функції, які дозволяють зменшити інтервал невизначеності в 1/ 0,618 раз.
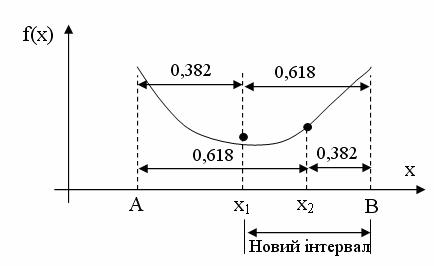
На цій стадії ще не видно переваг методу золотого перетину в порівнянні з методом дихотомії, однак їх добре видно при подальшому діленні інтервалу, так як виявляється, що одне із значень цільової функції, яке необхідно обчислити на наступному кроці, вже відомо. Тому, щоб зменшити невизначеність ще в 1/ 0,618 раз, потрібно додатково обчислити тільки одне значення цільової функції в точці, яка визначається правилом золотого перетину.
При n > 2 ефективність методу золотого перетину вища, ніж у метода дихотомії, так як при кожному наступному обчисленні цільової функції інтервал невизначеності скорочується в 1/ 0,618 раз. Після обчислення N значень цільової функції коефіцієнт дроблення інтервалу невизначеності складає
f = 0,618 N-1.
Метод золотого перетину дозволяє відмітити цікаву закономірність: найбільше скорочення наступних інтервалів невизначеності досягається при обчисленні цільової функції в точках, рівновіддалених від його центру. Якщо продовжувати таким чином і кожного разу, обчислюючи цільову функцію, скорочувати інтервал невизначеності, то будуть справедливими наступні відношення:
ZJ-2 = ZJ-1 + ZJ, 1
де ZJ довжина інтервалу невизначеності після обчислення J-го значення цільової функції.
На рис. 13.13 представлений алгоритм вибору наступної точки пошуку. Задана точність може, звичайно, змінюватися вибором значення. Для функції ![]() , пошук відбувався в інтервалі (0, 2).
, пошук відбувався в інтервалі (0, 2).
Істинний мінімум знаходиться в точці 1,76322211, де значення функції дорівнює -0, 0972601313.
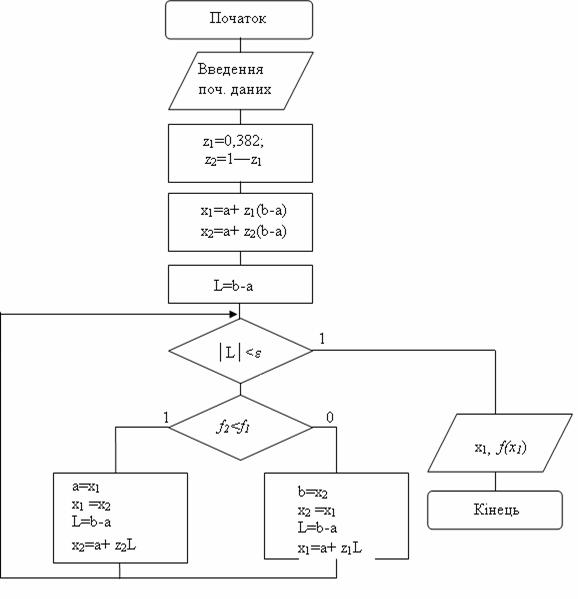
Рисунок 13.14 - Схема алгоритму метода „золотого перетину”
При розробці програм для рішення задач однопораметричної оптмізації використовують наступні співвідношення:
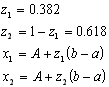
Припустимо, що потрібно визначити мінімум цільової функції як можна точніше, тобто з найменшим можливим інтервалом невизначеності, але при цьому можна виконати тільки ![]() обчислень функції. Як слід вибрати
обчислень функції. Як слід вибрати ![]() точок, в яких обчислюється функція? З першого погляду здається ясним, що не слід шукати рішення для всіх точок, які одержані в результаті експерименту. Навпаки, треба спробувати зробити так, щоб значення функції, отримані в попередніх експериментах, визначали положення наступних точок. Справді, знаючи значення функції, ми тим самим маємо інформацію про саму функцію і положення її мінімуму і використаємо цю інформацію в подальшому пошуку.
точок, в яких обчислюється функція? З першого погляду здається ясним, що не слід шукати рішення для всіх точок, які одержані в результаті експерименту. Навпаки, треба спробувати зробити так, щоб значення функції, отримані в попередніх експериментах, визначали положення наступних точок. Справді, знаючи значення функції, ми тим самим маємо інформацію про саму функцію і положення її мінімуму і використаємо цю інформацію в подальшому пошуку.
Припустимо, що є інтервал невизначеності ![]() і відомо значення функції
і відомо значення функції ![]() всередині цього інтервалу (див. рис. 13.15).
всередині цього інтервалу (див. рис. 13.15).
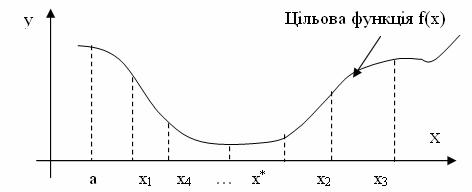
Якщо можна обчислити функцію всього один раз в точці ![]() , то де слід помістити точку
, то де слід помістити точку ![]() , для того щоб отримати найменший можливий інтервал невизначеності?
, для того щоб отримати найменший можливий інтервал невизначеності?
Припустимо ![]() і
і ![]() , причому
, причому![]() , як показано на рис. 13.15, і ці значення будуть фіксовані, якщо відомі
, як показано на рис. 13.15, і ці значення будуть фіксовані, якщо відомі ![]() і
і ![]() . Якщо
. Якщо ![]() знаходиться в інтервалі
знаходиться в інтервалі ![]() , то:
, то:
1. Якщо ![]() , то новим інтервалом невизначеності буде
, то новим інтервалом невизначеності буде ![]() довжиною
довжиною ![]() .
.
2. Якщо ![]() , те новим інтервалом невизначеності буде
, те новим інтервалом невизначеності буде ![]() довжиною
довжиною ![]() .
.
Оскільки невідомо, яка з цих ситуацій буде мати місце, виберемо ![]() таким чином, щоб зробити мінімальною найбільшу з довжин
таким чином, щоб зробити мінімальною найбільшу з довжин ![]() і
і ![]() . Досягнути цього можна, зробивши довжини
. Досягнути цього можна, зробивши довжини ![]() і
і ![]() рівними, тобто помістивши
рівними, тобто помістивши ![]() всередині інтервалу симетрично відносно точки
всередині інтервалу симетрично відносно точки ![]() , що вже лежить всередині інтервалу. Будь-яке інше положення точки
, що вже лежить всередині інтервалу. Будь-яке інше положення точки ![]() може призвести до того, що отриманий інтервал буде більший
може призвести до того, що отриманий інтервал буде більший ![]() . Помістивши
. Помістивши ![]() симетрично відносно
симетрично відносно ![]() , ми нічим не ризикуємо в будь-якому випадку.
, ми нічим не ризикуємо в будь-якому випадку.
Якщо виявиться, що можна виконати ще одне обчислення функції, то слід застосувати описану процедуру до інтервалу ![]() , в якому вже є значення функції, обчислене в точці
, в якому вже є значення функції, обчислене в точці ![]() . Отже, стратегія зрозуміла з самого початку. Потрібно помістити наступну точку всередині інтервалу невизначеності симетрично відносно точки, яка вже знаходиться там. Парадоксально, але, щоб зрозуміти, як потрібно починати обчислення, необхідно розібратися в тому, як його потрібно закінчувати.
. Отже, стратегія зрозуміла з самого початку. Потрібно помістити наступну точку всередині інтервалу невизначеності симетрично відносно точки, яка вже знаходиться там. Парадоксально, але, щоб зрозуміти, як потрібно починати обчислення, необхідно розібратися в тому, як його потрібно закінчувати.
На n- ому обчисленні n-у точку потрібно помістити симетрично по відношенню до (![]() -1)-ї точки. Положення цієї останньої точки в принципі залежить від нас. Для того щоб отримати найбільше зменшення інтервалу на даному етапі, слід поділити навпіл попередній інтервал. Тоді точка
-1)-ї точки. Положення цієї останньої точки в принципі залежить від нас. Для того щоб отримати найбільше зменшення інтервалу на даному етапі, слід поділити навпіл попередній інтервал. Тоді точка ![]() буде співпадати з точкою
буде співпадати з точкою ![]() . Однак при цьому ми не одержуємо жодної нової інформації. Звичайно точки
. Однак при цьому ми не одержуємо жодної нової інформації. Звичайно точки ![]() і
і ![]() знаходяться одна від одної на достатній відстані, щоб визначити, в якій половині, лівій чи правій, знаходиться інтервал невизначеності. Вони розміщуються на відстані
знаходяться одна від одної на достатній відстані, щоб визначити, в якій половині, лівій чи правій, знаходиться інтервал невизначеності. Вони розміщуються на відстані ![]() по обидві сторони від середини відрізка
по обидві сторони від середини відрізка ![]() ; можна самостійно задати величину
; можна самостійно задати величину ![]() або вибрати цю величину рівній мінімально можливій відстані між двома точками. (Припустимо, що в нашому прикладі інженер може регулювати температуру з інтервалом в 1С°, тому
або вибрати цю величину рівній мінімально можливій відстані між двома точками. (Припустимо, що в нашому прикладі інженер може регулювати температуру з інтервалом в 1С°, тому ![]() .)
.)
Інтервал невизначеності буде мати довжину ![]() , отже,
, отже, ![]() (рис. 13.16, нижня частина).
(рис. 13.16, нижня частина).
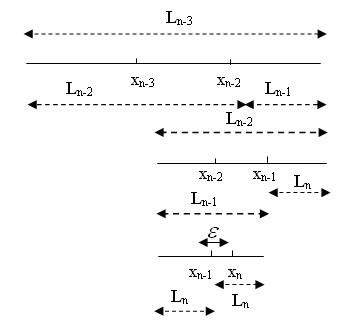
На попередньому етапі точки ![]() і
і ![]() повинні бути поміщені симетрично всередині інтервалу з
повинні бути поміщені симетрично всередині інтервалу з ![]() на відстані
на відстані ![]() від кінців цього інтервалу. Отже,
від кінців цього інтервалу. Отже, ![]() (рис. 13.16, середня частина).
(рис. 13.16, середня частина).
Зауваження. З рисунку зрозуміло, що на передостанньому етапі ![]() залишається в якості внутрішньої точки.
залишається в якості внутрішньої точки.![]()
Аналогічно
![]()
![]() . (рис. 13.16, верхня частина)
. (рис. 13.16, верхня частина)
В загальному випадку
Таким чином,
Якщо визначити послідовність чисел Фібоначчі наступним чином:
Якщо початковий інтервал
Тобто Отже, зробивши n обчислень функції, ми зменшимо початковий інтервал Якщо ми вже почали пошук, то його нескладно продовжити, використовуючи описане вище правило симетрії. Отже, необхідно знайти положення першої точки, що розміщується на відстані
Після того як знайдене положення першої точки, числа Фібоначчі більше не потрібні. Використане значення Таким чином, пошук методом Фібоначчі, названий так через появу при пошуку чисел Фібоначчі, є ітераційною процедурою. В процесі пошуку інтервалу
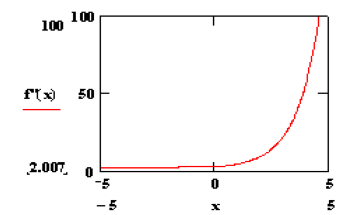
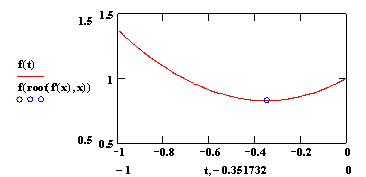
Якщо Приклад 1. Використати метод Фібоначчі для пошуку мінімуму функції Розв‘язок. Остаточний інтервал невизначеності має довжину З точністю до шостого знаку після коми мінімум досягається в точці Найкращими критеріями порівняння методів пошуку, які були описані вище, є їх ефективність і універсальність. Під ефективністю алгоритму розуміють число обчислень функції, необхідне для досягнення необхідного звуження інтервалу невизначеності. Із табл. 13.1 видно, що найкращим в цьому відношенні є метод Фібоначчі, а найгіршим – метод загального пошуку. Конструктор не з великим задоволенням використовує метод Фібоначчі, так як при його застосуванні необхідно заздалегідь задавати число обчислень значень функції. Однак він може скористатися методом золотого перетину. Як правило, методи Фібоначчі і золотого перетину, володіють високою ефективністю, найбільш підходять для розв’язку одновимірних унімодальних задач оптимізації. Універсальність алгоритму означає, що його можна легко застосувати для розв’язку самих різноманітних задач. В цьому відношенні метод Фібоначчі, поступається іншим, так як потребує окремого обчислення положення точок, в яких будуть визначатися значення цільової функції на кожному новому кроці. Цим приходиться розплачуватися за підвищення ефективності метода. З точки зору універсальності малоефективний метод загального пошуку має по крайній мірі одну перевагу – його можна з успіхом застосовувати і для неунімодальних функцій, якщо вони достатньо гладкі. Нерідко заздалегідь не відомо, чи є розглянута цільова функція унімодальною. В таких випадках слід використати декілька різних алгоритмів і подивитись, чи дають вони усі один і той самий оптимум. Звідси витікає важливий висновок, який слід мати на увазі, розв’язуючи задачі оптимізації: не існує універсального алгоритму, який дозволяв би розв’язувати будь-які задачі. Вирішуючи складні задачі оптимізації, слід користуватися різними методами, так як це дозволяє збільшити долю вигідних розв’язків. Кількість обчислень цільової функції N Загальний пошук Ділення відрізка навпіл Метод дихотомії Метод золотого перетину Метод Фібоначчі 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 1,0 0,667 0,500 0,400 0,333 0,286 0,250 0,222 0,200 0,182 0,167 0,154 0,143 0,133 0,125 0,118 0,111 0,105 0,100 0,095 1,0 - 0,500 - 0,250 - 0,125 - 0,0625 - 0,0312 - 0,0156 - 0,00781 - 0,00391 - 0,00195 - 1,0 0,500 - 0,250 - 0,125 - 0,0625 - 0,0312 - 0,0156 - 0,00781 - 0,00391 - 0,00195 - 0,000976 1,0 0,618 0,382 0,236 0,146 0,090 0,056 0,345 0,0213 0,0132 0,00813 0,00502 0,00311 0,00192 0,00119 0,000733 0,000453 0,000280 0,000173 0,000107 1,0 0,500 0,333 0,200 0,125 0,077 0,048 0,0294 0,0182 0,0112 0,00694 0,00429 0,00265 0,00164 0,00101 0,000626 0,000387 0,000239 0,000148 0,0000913 Приклад 1. Одновимірна мінімізація в середовищі Mathcad Для знаходження мінімуму одновимірної функції в середовищі Mathcad використовується функція root(f(var1, var2, ...),var1, [a, b]) – повертає змінну var1, що лежить між a і b, в якій функція, що розв’язується дорівнює нулю. Параметри: f – рівняння, яке потрібно розв’язати; var1 – корінь рівняння; [a, b] – відрізок, на якому шукається розв’язок рівняння. Наприклад, необхідно знайти мінімум гладкої унімодальної функції у=х2+ех, використовуючи необхідну умову мінімуму. Визначимо цільову функцію Визначимо першу похідну цільової функції Визначимо другу похідну цільової функції Достатня умова унімодальності (f''(x)>0) виконана Мінімум гладкої функції досягається в стаціонарній точці (f'(x)=0). Розв’яжемо рівняння f'(x)=0, використовуючи функцію root; початкове наближення кореня нехай дорівнює нулю (х=0) Точка мінімуму х=-0.351732 Значення функції в точці мінімуму Підтвердимо результати обчислень графічно 1. Щуп Т. Решение инженерных задач на ЭВМ. – М.: Мир, 1982. – 235с. 2. Бахвалов Н. С. Численные методы . Т. И. Анализ, алгебра, обычные диференциальные уравнения. – М.: Наука, 1975. – 631 с. 3. Ляшенко М.Я., Головань М.С. Чисельні методи: Підручник. Либідь. 1996. – 288 с. 4. Крылов В. И. и др. Численные методы . – М.: Наука, 1978. – 1979. – Т. 2. – 400 с. 5. Форсайт Дж., Малькольм., Моулер Р. Машинные методы математических вычислений. – М.: Мир, 1980. – 279c. 6. Д. Мэтьюз, Г. Цинк, Д. Куртис. Численне методы. Использование Matlab, –М. Издательский дом “Вильямс”, 2001. – 720 с. 720 с. 7. Гил Ф., Мюрей У. Численные методы условной оптимизации. – М.: Мир, 1977. – 290 с. 8. Василев Ф. П. Лекции по методам решения експериментальных задач. – М.: Изд – во Моск. Ун – то, 1984. – 374 с. 9. Полак Е. Численные методы оптимизации. – М. : Мир, 1974. 10. Пшеничний Б. Н., Данилин Ю. М. Численные методы в екстремальных задачах. – М. : Наука, 1975. 11. Моделирование и оптимизация на ЭВМ радиоэлектронных устройств / Под ред. З. М. Бенесона. – М. : Радио и связь, 1981. – 272 с. 12. И.В. Кузьмин, М.М. Биков, С.М. Москвина, А.И. Кузьмин. Методы оптимизации сложных систем. – Винница: ВДТУ, 2003. – 165с. 1. В чому полягає властивість унімодальності функцій і в чому полягає важність цієї властивості при розв’язку задач оптимізації з однією змінною? 2. Якщо точка цільової функції задовольняє достатнім умовам існування локального мінімума, то як встановити чи є цей мінімум глобальним? 3. Чи є методи виключення інтервалів в цілому більш ефективними, ніж методи точкового оцінювання? Чому? 4. При реалізації пошукових алгоритмів на ЕОМ в якості умови закінчення ітераційного процесу використовуються як аналіз абсолютної величини різниці поточних значень кінців відрізка дослідження, так і абсолютної величини різниці поточних значень цільової функції. Чи можлива ситуація, коли результат однієї з перевірок вказує на збіжність до точки мінімума, тоді як отримана точка в дійсності мінімуму не відповідає. Поясніть відповідь рисунком. 5. Задані наступні функції однієї змінної: а) б) Для кожної з заданих функцій знайдіть:![]() при 1
при 1![]() , (13.2)
, (13.2)
![]() ,
,
![]() ,
,
![]() і т.д.
і т.д.
![]()
![]() та
та ![]() для
для ![]() тоді
тоді![]() ,
, ![]() (13.3)
(13.3)
![]() має довжину
має довжину ![]() , то
, то![]() .
.![]() . (13.4)
. (13.4)
![]() невизначеності в
невизначеності в ![]() раз у порівнянні з його початковою довжиною (нехтуючи
раз у порівнянні з його початковою довжиною (нехтуючи ![]() ), і це буде найкращий результат.
), і це буде найкращий результат.![]() від одного з кінців початкового інтервалу, причому не важливо, від якого кінця, оскільки друга точка розміщується згідно правила симетрії на відстані
від одного з кінців початкового інтервалу, причому не важливо, від якого кінця, оскільки друга точка розміщується згідно правила симетрії на відстані ![]() від другого кінця інтервалу:
від другого кінця інтервалу: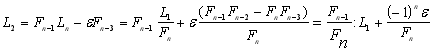 . (13.5)
. (13.5)
![]() може бути визначене з практичних міркувань. Воно повинне бути менше
може бути визначене з практичних міркувань. Воно повинне бути менше ![]() , в протилежному випадку ми будемо марно витрачати час на обчислення функції.
, в протилежному випадку ми будемо марно витрачати час на обчислення функції. ![]() з точкою
з точкою ![]() , що вже лежить в цьому інтервалі, наступна точка
, що вже лежить в цьому інтервалі, наступна точка ![]() завжди вибирається такою, що
завжди вибирається такою, що ![]() або
або ![]() , тобто
, тобто![]() . (13.6)
. (13.6)
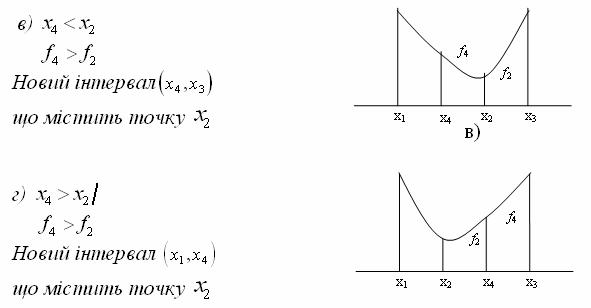
![]() та
та ![]() , тоді можна розглянути чотири випадки (рис. 13.17).
, тоді можна розглянути чотири випадки (рис. 13.17). 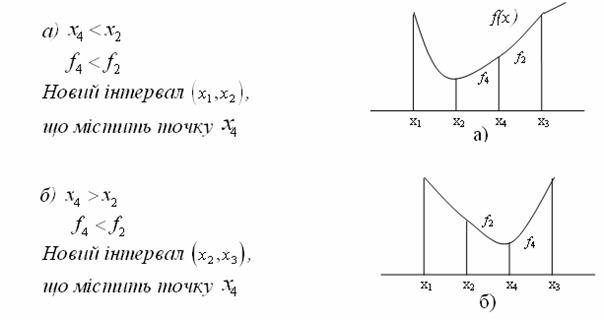
![]() в інтервалі (0,1) при 10-кратному обчисленні функції.
в інтервалі (0,1) при 10-кратному обчисленні функції.![]()
![]() , і в цій точці
, і в цій точці![]()
![]()
![]() .
.
13.6 Порівняння методів одновимірного пошуку
![]()
![]()
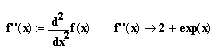
![]()
![]()
Література
Питання та задачі до самостійної роботи
![]() ;
;![]() .
.
6. Встановіть області, в яких наступна функція випукла чи вогнута: ![]() . Знайдіть глобальний максимум і глобальний мінімум цієї функції.
. Знайдіть глобальний максимум і глобальний мінімум цієї функції.
7. В чому суть алгоритму метода дихотомії? Складіть схему алгоритма цього метода. Виберіть і обґрунтуйте умову виходу з ітераційного циклу.
8. Дослідіть функцію ![]() в інтервалі -4
в інтервалі -4![]() 4. Знайдіть локальні мінімуми, локальні максимуми, глобальний мінімум і глобальний максимум f в заданому інтервалі.
4. Знайдіть локальні мінімуми, локальні максимуми, глобальний мінімум і глобальний максимум f в заданому інтервалі.
9. В чому сутність алгоритму метода Фібоначчі? Складіть схему алгоритма метода, наведіть основну математичну модель метода.
10. Розробіть програму для ЕОМ, яка реалізує пошук оптимуму за методом золотого перетину і методом Фібоначчі для функції ![]() в інтервалі
в інтервалі ![]() . Порівняйте результуючі інтервали пошуку, які отримані за допомогою перерахованих методів.
. Порівняйте результуючі інтервали пошуку, які отримані за допомогою перерахованих методів.