У цій частині розглядаються фундаментальні поняття і конкретні методи, які використовують при пошуку безумовних мінімумів функцій декількох змінних. Викладене ґрунтується на матеріалі розділу 3, оскільки одномірні методи відіграють дуже важливу роль при дослідженні функції декількох змінних.
На перший погляд може показатися, що відмінність між методами багатовимірного і одномірного пошуку полягає лише в тому, що перші вимагають більшого об'єму обчислень, і, що в принципі методи, які придатні для функцій однієї змінної, можна застосовувати і для функцій багатьох змінних. Однак це не так, оскільки багатовимірний простір якісно відрізняється від одномірного. Передусім зі збільшенням числа вимірів зменшується ймовірність унімодальності цільової функції. Крім того, безліч елементів, які утворюють багатовимірний простір, значно потужніші множини елементів одномірного простору. Об'єм обчислень, які необхідні для звуження інтервалу невизначеності в багатовимірному просторі, є степеневою функцією, показник якої рівний розмірності простору. Так, якщо в випадку одномірного простору для досягнення
=0,1 вимагається обчислити 19 значень цільової функції, то у випадку двомірного простору це число складає 361, тримірного – 6859, чотиримірного – 130321, а п'ятимірного – 2476099! Оскільки при виборі оптимальної конструкції нерідко потрібно мати діло з п'ятьма і більше змінними, серйозність труднощів, зумовлених багатовимірністю, стає очевидною.
Спочатку розглянемо питання аналізу (в статиці( з використовуванням положення лінійної алгебри і диференційного обчислення, а також умови, які (в достатньо загальних можливих випадках) дозволяють ідентифікувати точки оптимуму. Такі умови використовують для перевірки обраних точок і дають можливість з’ясувати, чи є ці точки точками мінімуму чи сідловими точками. При цьому задача вибору вказаних точок залишається за межами цього аналізу; основна увага віддається розв’язанню питання про те, чи відповідають досліджувані точки розв’язку багатовимірної задачі безумовної оптимізації, у якій вимагається мінімізувати f(x) , xОRN, (14.1) коли обмеження відсутні на х , де х - вектор керованих змінних розмірності N, f — скалярна цільова функція. Звичайно допускається, що хі (для всіх значень = 1,2,3,...,N) можуть приймати будь-які значення, хоча інколи в практичних застосуваннях область значень х обирається в вигляді дискретної множини. Крім того, часто зручно допускати, що функція f і її похідні існують і неперервні скрізь, хоча ми знаєм, що оптимуми можуть досягати в точках розриву f чи її градієнта
. (14.1)
Потрібно мати на увазі, що функція f може приймати мінімальні значення в точці 
, в якій f чи 
f розриваються. Крім того, цієї точки 
може не існувати.
Для того, щоб побудувати систему конструктивних критеріїв оптимальності, необхідно (якнайменше на першій стадії дослідження) виключити із розгляду подібні ситуації, які дуже ускладнюють аналіз. У ряді випадків приходиться обмежуватись лише ідентифікацією локальних оптимумів, оскільки нелінійна цільова функція f не завжди має випуклий характер, може бути мультимодальною. На рис. 14.1 відображенні лінії рівняння функції Хіммельблау
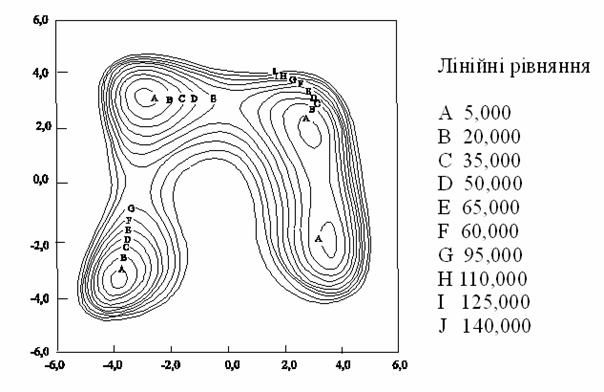
f(x)=[x12+x2-11]2+[x1+x22-7]2, (14.2)
неважко побачити , що ця функція має чотири різних мінімуму.
Далі підійдемо до питання аналізу (в динаміці(, яке формулюється таким чином: якщо точка х(0) не задовольняє вимогам, які
Функція Хіммельблау:
(14.3)
визначаються критеріями оптимальності, то як отримати (добре( нове наближення х(1) до розв’язку х? Спроба дати відповідь на це питання приводить до необхідності розгляду ряду методів. Методи, які розглядаються, класифікуються у відповідності з тим, чи використовується інформація про похідні досліджуваної функції.
Розглянемо умови, які дозволяють характеризувати (тобто класифікувати) точки простору керованих змінних. Критерії оптимальності необхідні для розпізнавання рішень і, крім того, складають основу більшості методів пошуку рішень, що використовуються.
Для цього розглянемо розклад Тейлора для функції декількох змінних :
(14.4)
де - точка розкладення із простору RN; 
х=х- — величина зміни х; f(x) — N-мірний вектор - стовпчик перших похідних f(x), обчислених в точці ; 2f()=Hf() — симетрична матриця порядку NґN других частинних похідних f(x), вирахуваних у точці . (Цю матрицю часто називають матрицею Гессе. Її елемент, розташований на перетині i-й строчки і j-го стовпчика, дорівнює J2f/dxiJxj.) O3(x)- сума всіх членів розкладу, які мають порядок по х вище другого. Нехтуючи членами найвищих порядків (тобто виключаючи О3(х)), визначимо величину зміни цільової функції f(x), відповідно довільній зміні х:
. (14.5)
Нагадаємо, що по визначенню у всіх точках із околу точки мінімуму цільова функція приймає значення, які вище мінімального, тобто має місце нерівність
)і0. (14.6)
Точка є точкою глобального мінімуму, якщо нерівність (14.6) виконується для всіх хОRN; такі точки будемо позначати через х**. Коли формула (14.6) справедлива лише в деякому d-околі точки , т.б. для всіх х, таких, що (х-(d при заданому d>0, то є точкою локального мінімуму, чи х*. Якщо
)Ј0 , (14.7)
то є точкою максимуму ( локального чи глобального у відповідності з даним вище визначенням). Виключення знака рівності із формул (14.6) і (14.7) дозволяє визначити точку строгого мінімуму чи максимуму. В тому випадку, коли 
приймає як додатне, так і від’ємне, так і нульове значення в залежності від вибору точок із d-околу, точка являє собою сідлову точку.
Повернемось до рівняння (14.5) і згадаємо про висунуте раніше припущення про те, що f(x), 
і 
f(x) існують і неперервні для всіх хОRN. Як випливає з формули (14.5), для того щоб знак 
не змінювався при довільній зміні 
, градієнт f() повинен дорівнювати нулю, тобто повинна бути стаціонарною точкою. В протилежному випадку різниця f може приймати додатні чи від’ємні значення в залежності від знаків () і 
. Таким чином, точка повинна задовольняти умові стаціонарності
()=0 , (14.8)
і формула (14.5) приймає такий вигляд :
) . (14.9)
Звідси видно, що знак 
визначається квадратичною формою
)
, (14.10)
чи Q(x)=zTAz. (14.11)
Із лінійної алгебри ми знаємо, що:
А- додатньо визначена матриця, якщо Q(z)>0 для любих z;
А- додатньо напіввизначена матриця, якщо Q(z)і0 для любих z;
А- від’ємно визначена матриця, якщо Q(z)<0 для любих z ;
А- від’ємно напіввизначена матриця, якщо Q(z)Ј0 для любих z ;
A-невизначена матриця, якщо Q(z)>0 для деяких z і Q(z)<0 для останніх z.
Із (14.11) видно, що стаціонарна точка є
- точкою мінімуму, якщо 
) — додатньо напіввизначена матриця;
- точкою максимуму, якщо 
) — від’ємно напіввизначена матриця;
- сідлова точка, якщо ) > (або <) 0 — невизначена матриця.
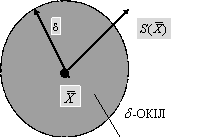
Крім того, іноді корисно провести аналіз стаціонарної точки в деякому іншому аспекті. Розглянемо стаціонарну точку разом з оточуючим її d- колом і векторами, що виходять із точки (рис. 14.2). При цьому
s(). (14.12)
Шляхом відповідного вибору a і s можливо побудувати всі точки 
із кола точки . Підстановка (14.12) в (14.9) дає формулу
. (14.13)
Тепер за допомогою (14.11) і (14.12) можливо класифікувати s(x) як напрямок спуску, напрямок підйому чи напрямок загального вигляду. Якщо напрямок спуску знайти не вдається, то є точкою локального мінімуму х*, що відповідає випадку, коли 
- додатньо напіввизначена матриця.
Теорема 1. Необхідні умови
Для наявності в точці х* локального мінімуму необхідно, щоб виконувалась рівність
(14.14а)
і матриця 
була додатньо напіввизначеною:
0. (14.14б)
Теорема 2. Достатні умови
Якщо
(14.15а)
і матриця 
додатньо визначена, то
> 0. (14.15б)
Доведення цих теорем витікає із наведеного вище судження. Звичайно доводиться обмежуватись находженням локального мінімуму; разом з тим, якщо можна показати, що 
для всіх х, то f(x) називають випуклою функцією, а локальний мінімум називають глобальним.
Приклад 14.1. Критерії оптимальності
Розглянемо функцію
,
лінії рівня якої зображені на рис. 14.3.
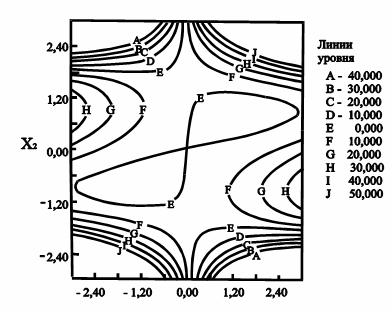
Треба класифікувати точку =[0,0]T .
Розв’язок.
,
,
.
Звідси, точка — стаціонарна.
,
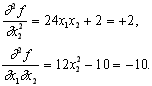
Звідси,
Матриця 
є невизначеною, так як квадратична форма 
приймає додатнє значення при z=(0,1) і від’ємне значення при z=(1,1). Тому представляє собою сідлову точку, що і відображено на рис. 14.3.
В багатьох алгоритмах багатовимірної оптимізації так чи інакше використовується інформація про градієнти. Проілюструємо це положення наступним простим прикладом. Представимо собі, що альпіністу зав’язали очі і сказали, що він повинен добратися до вершини “унімодальної” гори. Навіть якщо він не буде нічого бачити, він може це зробити, якщо весь час буде рухатися вверх. Хоча будь-яка тропа, яка веде вверх, в кінці-кінців приведе його до вершини, найкоротшою з них буде найкрутіша, якщо, правда, альпініст не наштовхнеться на вертикальний обрив, який необхідно буде обійти. (Математичним еквівалентом обриву на поверхні, яку створює цільова функція, являються ті її місця, де поставлені умовні обмеження). Уявімо, що задача оптимізації не містить обмежень. Пізніше ми включимо їх в схему пошуку. Метод оптимізації, в основі якого лежить ідея руху по самій крутій тропі, називається методом найшвидшого підйому або найшвидшого спуску. Вектор градієнта перпендикулярний лінії рівня і вказує напрямок до нової точки в просторі проектування. Відмітимо, що градієнтний метод на відміну від методу дотичної до лінії рівня можна використовувати до будь-якої унімодальної функції, а не тільки тих, у яких ця властивість явно виражена.
Щоб краще зрозуміти ідею градієнтних методів, більш конкретно зупинимося на властивостях градієнтів. Розглянемо систему незалежних одиничних векторів е1, е2, е3, …, еN, які направлені в здовж вісей координат x1, x2, x3, …, xN, які є в той же час проектними параметрами. Вектор градієнта довільної цільової функції F = (x1, x2, x3, …, xN,) має вигляд
,
де частинні похідні обчислюються в точці, яка розглядається. Цей вектор направлений вверх, в напрямку підйому; обернений йому вектор вказує напрямок спуска. Одиничний вектор градієнта часто представляють у вигляді
,
де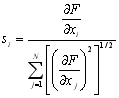 
. (14.16)
Іноді характер цільової функції буває достатньо добре відомий, щоб можна було обчислити компоненти вектора градієнта шляхом безпосереднього диференціювання. Якщо таким способом частинні похідні отримати неможливо, то можна знайти їх наближені значення в безпосередньому околі точки, яка розглядається:
.
Тут 
- невелике зміщення в напрямку хi. Цю формулу часто називають “наближенням січної”. Отриману інформацію про напрямок градієнта можна використовувати різним чином для побудови алгоритму пошуку.
Постановка задачі оптимізації градієнтними методами: мінімізація функції F (x1, x2, x3, …, xN) з N проектними параметрами за допомогою ЕОМ розв’язується ітераційними методами. Розв’язок задачі починається з вибору початкових значень 
(i = 1, 2, …, N), які за звичай визначаються із умов розв’язуємої задачі, і потім будують послідовні наближення, використовуючи ітераційну формулу, яку отримуємо з формули (14.12):
, (i = 1, 2, …, N; j = 0, 1, 2, …), (14.17)
де 
- величина кроку ітерації по кожному з параметрів 
;
- параметр вибору “напрямку”, який звичайно визначається за формулою (14.12).
Дана формула забезпечує збіжність досліджуваної функції до деякого рішення 
при 
. Величина кроку 
на кожній j-ій ітерації визначається одним з методів оптимізації однопараметричної оптимізації, наприклад методом ділення відрізка навпіл або методом “золотого перетину” або Фібоначчі.
В деяких методах пошуку інформація про градієнт використовується для ведення одномірного пошуку в напрямку найшвидшого підйому або спуску, причому використовується співвідношення
, (14.18)
де 
- величина кроку, значення якого визначаються в напрямку градієнта.
Отримавши одномірний оптимум в напрямку даного градієнта, знаходять новий градієнт і повторюють процес до тих пір, поки наступні обчислення дозволяють покращувати отриманий результат. Головна перевага цього метода полягає в тому, що параметр можна використовувати в якості незалежної змінної для пошуку за методом Фібоначчі, і це забезпечує високу ефективність метода. Інша важлива перевага методів, які розглядаються, полягає в тому, що вони дозволяють відходити від сідловин точок поверхні, яка описується цільовою функцією (рис. 14.4).
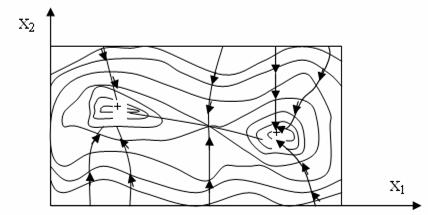
Відмітимо, однак, що, як видно з рисунку, для мультимодальних функцій градієнтні методи дозволяють знайти лише локальний оптимум. Тому, якщо характер поверхні недостатньо добре відомий, то слід випробувати декілька початкових точок і переконатися, що в усіх випадках отримується одне й те ж оптимальне рішення. Іншою причиною, яка знижує ефективність градієнтних методів, являються злами ліній рівня цільової функції. Так як такі точки відповідають розриву в нахилі лінії контура, то тут можливі помилки в визначенні напрямку подальшого пошуку. Тому пошук може уповільнитися і іти зигзагами поперек лінії зламу, а час необхідний для отримання рішення, буде на стільки великим, що рахунок прийдеться припинити. В дійсності більшість досліджуємих поверхонь має одну або більше ліній зламу, які нерідко проходять через точку оптимуму. Тому, наткнувшись на лінію зламу, слід в подальшому рухатися вздовж неї.
Даний метод заснований на використанні ітераційної формули
,
де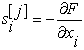 
, причому усі похідні обчислюються при 
;
- величина кроку, значення якого змінюється (зменшується або обчислюється) методом половинного ділення.
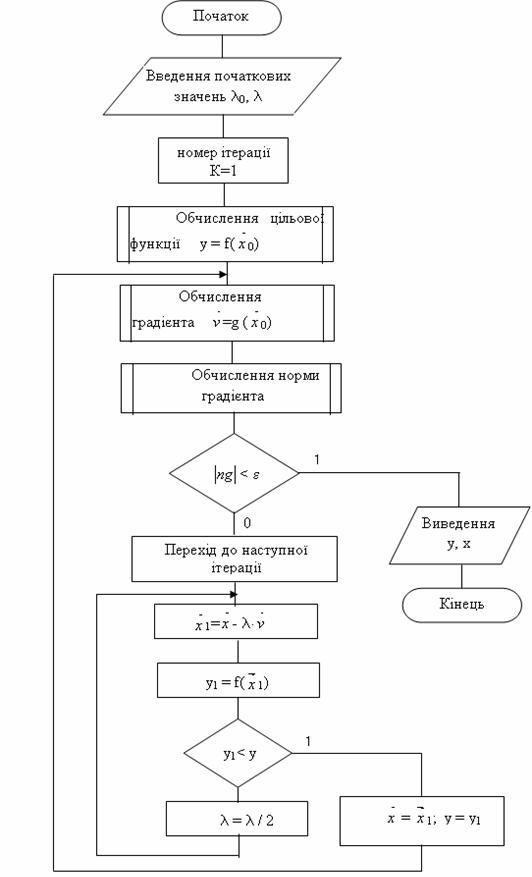
Алгоритм методу найшвидшого спуску:
1. Обираємо початкові значення координат вектора 
і початкові значення кроку ітераційного процесу , які звичайно обираються з умов розв’язуємої конкретної задачі. Хоча загальних правил вибору 
немає, однак якщо є додаткова інформація про область розташування мінімуму цільової функції, то обираємо в цій області.
2. Задаємо номер ітерації к = 1.
3. Обчислюємо значення цільової функції в точці з координатами .
4. Обчислюємо значення градієнта 
.
5. Обчислюємо норму вектора градієнта NG.
6. Якщо |NG| < заданої 
, то ітераційний процес закінчується і оптимум знайдений.
7. Якщо умова |NG| < не виконується, то визначаються нові координати вектора 
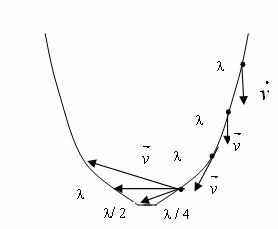
, які отримуються при русі до мінімуму цільової функції з кроком (рис. 14.5).
8. Порівнюємо два значення цільової функції в двох точках з координатами векторів 
і за формулою
, (14.31)
9. Якщо умова не виконується, то крок був вибраний невірно, тобто з цим кроком перескочили через оптимум і крок потрібно зменшити, наприклад в два рази 
і переходимо до пункту 7 (рис. 14.5).
10. Якщо умова (14.31) виконується, то запам’ятовуємо координати вектора і переходимо до пункту 4.
Схема алгоритму описаного методу представлена на рис. 14.6.
Цей метод дозволяє знайти мінімум нелінійної цільової функції багатьох змінних вигляду
при відсутності обмежень. Метод заснований на застосуванні часткових похідних цільової функції по незалежним змінним і перевизначений для дослідження унімодальних функцій. За його допомогою можна досліджувати і мультимодальні функції, однак в цьому випадку слідує брати декілька вхідних точок і перевіряти, однаково чи в усіх випадках рішення. Схема алгоритму метода Флетчера – Рівса представлена на рис.14.6.
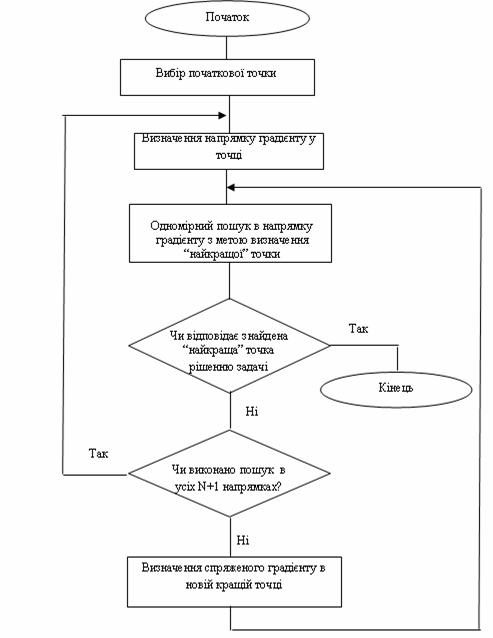
Виконується він наступним чином. Спочатку вибирається підхожа початкова точка простору проектування й шляхом обчислення компонент вектора градієнта визначається напрямок найшвидшого спуску. Індекс 
=1 відповідає вхідній точці. Після цього в напрямку найшвидшого спуску ведеться одномірний пошук по формулі
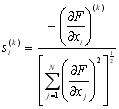, і = 1, 2, ..., N,
, і = 1, 2, ..., N,
де – зміщення в напрямку вектора градієнту. Знайшовши мінімум в цьому напрямку, визначають напрямки нових одиничних векторів, які дещо відрізняються від напрямку нового вектора градієнту і являють собою лінійні комбінації вектору градієнту на даному кроці і вектора градієнту, отриманого на попередньому кроці. Нові компоненти одиничних векторів записуються у вигляді
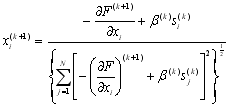, і = 1, 2, ..., N, (14.19)
де
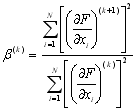. (14.20)
Індекс 
вказує на послідовність обчислень в процесі ітерацій. Нові напрямки називаються «спряженими» і відповідають поточній локальній квадратичній апроксимації функції, а фактично представляють собою рух по дну яру (рис. 14.7).
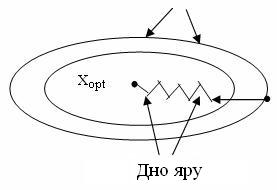
Рисунок 14.7 – Зміна напрямків руху 
по дну яру
Після цього по новому напрямку (іншому склону яру) проводять одномірний пошук і, знайшовши мінімум, перевіряють, чи досягнутий необхідний ступінь збіжності. Якщо перевірка показує, що це так, то рахунок припиняється. В протилежному випадку визначають нові спряжені напрямки,
збільшують на одиницю і продовжують процес до тих пір, доки не буде забезпечена збіжність або доки пошук не буде проведений по всім 
+1 напрямкам. Закінчивши цикл пошуку по
+1 напрямкам, починають новий цикл, в якому знову використовується напрямок найшвидшого спуску. Особливість цього алгоритму полягає в тому, що він дозволяє використати переваги градієнтних методів, які проявляються при дослідженні цільової функції з перервними похідними. Так як
+1 напрямків пошуку другої сукупності відрізняються від напрямків одиничних векторів градієнту, то пошук не «зависає на перегині», а йде вздовж лінії, яка з'єднує точки перегинів лінії рівня, яка, як правило, проходить через точку оптимуму. Взагалі можна стверджувати, що методи, основані на визначенні нових напрямків пошуку на основі накопичених даних про локальну поведінку функції, по самій своїй природі більш ефективні, ніж методи, в яких напрямок пошуку задається заздалегідь. Саме тому метод Флетчера – Рівса володіє більшими перевагами у порівнянні з методами найшвидшого спуску або підйому. Його недолік полягає в тому, що, він є складнішим ніж вказані методи, він вимагає розробки більш складних програм.
Метод Девідона – Флетчера – Пауела являє собою алгоритм оптимізації, пристосований для відшукання безумовного мінімуму цільової функції, яка залежить від декількох змінних і яка має вигляд
(14.21)
Необхідні часткові похідні цільової функції по незалежним змінним. Оскільки в основі методу лежить допущення про унімодальність цільової функції, в тих випадках, коли є підстави припускати, що вона не є такою, потрібно брати декілька вхідних точок. На рис. 14.9 представлена схема алгоритму методу Девідона – Флетчера – Пауела. Спочатку в просторі проектування вибирають придатну початкову точку. Після цього, обчислюючи складові вектора градієнту визначають напрямок пошуку.
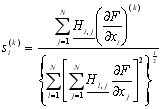, i = 1, 2, ..., N,
тут – номер ітерації, а
– елементи симетричної позитивно визначеної матриці розмірності N
N. В процесі ітерацій ця матриця перетворюється в матрицю, зворотну матриці Гессе, елементами якої є другі часткові похідні цільової функції. Оскільки звичайно матриця заздалегідь невідома, то в якості початкової можна скористуватися будь-якою симетричною позитивно визначеною матрицею. Як правило, беруть найпростішу з них – одиничну матрицю. В цьому випадку пошук починається вздовж лінії найшвидшого спуску.
Одномірний пошук ведеться вздовж вхідного напрямку у відповідності з співвідношенням
(14.22)
де 
– величина кроку в напрямку пошуку. Знайшовши одновимірний оптимум, перевіряють результат на збіжність і, якщо вона досягнута, пошук припиняють. В протилежному випадку для подальшого пошуку вибирають новий напрямок, причому використовують колишнє співвідношення і нову матрицю
, що визначається формулою
(14.23)
Елементи матриць
і 
, які мають розмірність N
N обчислюються по формулам
(14.24)
(14.25)
де верхнім індексом 
позначені транспоновані матриці, а
і
– відповідно вектори - стовпці різниць значень
і градієнтів в двох точках. Вектори - стовпці визначаються виразами
У відповідності з правилами матричного обчислення числівники виразів для 
і
являють собою матриці розмірності N
N, а знаменники є скалярами. Визначивши новий напрямок пошуку, проводять одномірний пошук і продовжують ітераційний процес. При виконанні алгоритму, який описується, пошук після першої спроби ведеться в тих напрямках, в яких цільова функція в найближчому околі має значення, які наближаються до оптимального.
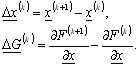
Лише в рідких випадках ці напрямки співпадають з напрямком градієнту. Тому даний алгоритм часто називають методом «відхиленого» градієнту. Вказана властивість методу Девідона – Флетчера – Пауела дозволяє обходити труднощі, які зв'язані з розривами похідних в просторі проектування. Широко розповсюджена думка, що цей метод є найбільш ефективним з усіх градієнтних методів. На відміну від методу Флетчера – Рівса він дає повну інформацію про кривизну поверхні цільової функції в точці мінімуму, однак при цьому вимагається більший об’єм пам'яті і більший час лічби для обробки матриці 
.
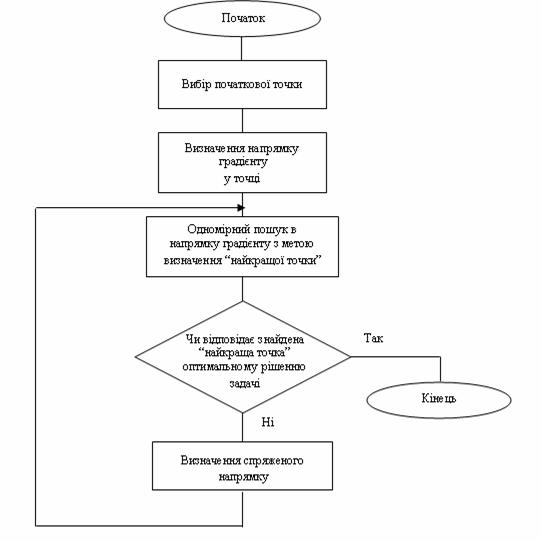
Цей метод полегшує пошук і не вимагає обчислення похідних. Пошук ведеться вздовж ліній розриву похідних у припущенні, що зміщення в просторі проектування, які опинилися вдалими на ранній стадії пошуку, можуть призвести до успіху і на його більш пізніх стадіях. Метод Хука – Дживса перевизначений для пошуку мінімуму унімодальної функції багатьох змінних
(14.26)
при відсутності обмежень. На рис. 14.10 представлена схема алгоритму цього методу.
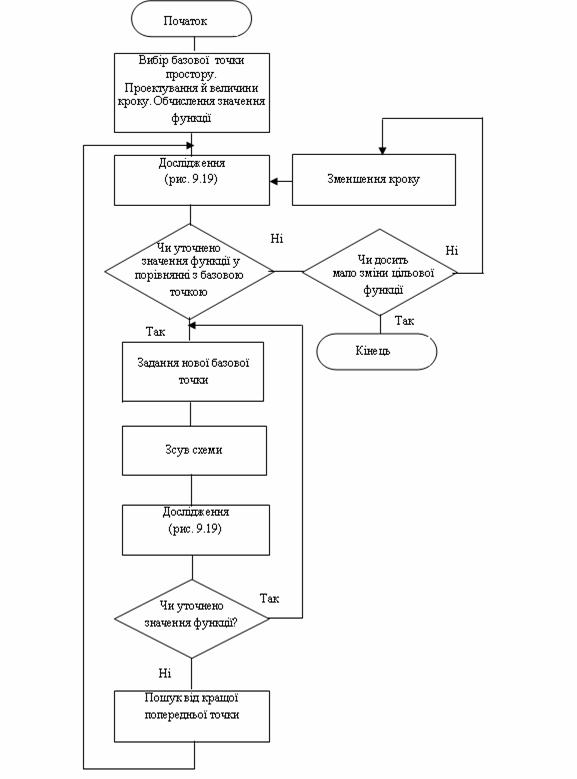
Рисунок 14.10 - Схема алгоритму методу конфігурацій Хука – Дживса
Виконується він наступним чином. Спочатку вибирається вхідна базова точка простору проектування і величини кроків, що будуть використані при дослідженні функції. Після цього у відповідності зі схемою рис. 14.11 проводиться дослідження із заданими приростом у напрямках, відповідних всім незалежним змінним.
Там, де отримано уточнене значення функції, розміщують нову тимчасову базову точку. Закінчивши етап дослідження, вибирають нову базову точку і виконують «зрушення схеми». Ця операція полягає в екстраполяції вздовж лінії, що з'єднує нову і колишню базові точки. Відстань зсуву за нову базову точку декілька перевищує відстань між двома колишніми базовими точками. Математично екстраполяція визначається формулою (14.27)
(14.27)
де
– нова тимчасова базова точка, або «точка зростання», 
– змінний індекс,
– порядковий номер стадії пошуку, а 
– коефіцієнт підсилення, що більше або рівний одиниці. Після цього досліджують окіл нової тимчасової базової точки, щоб з'ясувати, чи не містить вона точку, прийнявши яку за наступну базову можна наблизитися до оптимального рішення. Цей пошук також ведеться по схемі, яка показана на рис. 14.11.
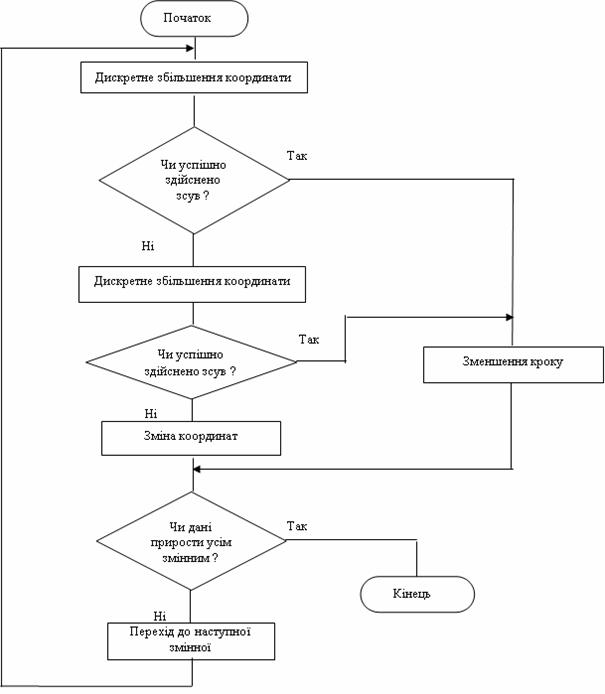
Якщо знайдена тимчасова точка зростання або одна з сусідніх з нею точок має перевагу перед іншими, то вся процедура повторюється з використанням її в якості базової. Завдяки введенню коефіцієнта підсилення, кожне наступне дослідження околу точки здійснюється на все більшому і більшому віддаленні від вхідної точки до тих пір, доки в процесі пошуку не виявиться пройденим пік або лінія розриву похідної. В цьому випадку вертаються до попередньої «кращої базової точки», звужують область дослідження і повторюють весь процес знову. Якщо крок, який зменшується, послідовно виявляється меншим за деяку заздалегідь задану величину і при цьому відсутня помітна зміна значення цільової функції, пошук припиняється. Після декількох змін напрямку пошуку метод Хука – Дживса забезпечує збіг розподілу розрахункових точок з лінією розриву похідних. Звичайно після завершення вибору схеми пошуку зсуву на кожному наступному кроці збільшується, доки не перевищить величину вхідного кроку в 10 або навіть в 100 раз. Тому у випадку, коли зрушення виявляється невдалим, єдиний засіб продовжити пошук — повернутися до найбільш вдалої з базових точок і почати усе спочатку. Той факт, що даний алгоритм володіє властивістю «прискорюватися», сприяє підвищенню його загальної ефективності. Друга перевага методу Хука – Дживса – можливість отримання за його допомогою наближеного рішення, якість якого безупинно підвищується на всіх стадіях чисельного рішення. Особливо явно переваги подібних засобів виявляються при відшуканні екстремумів на гіперповерхнях, які містять глибокі вузькі западини, тобто тоді, коли градієнтні методи неефективні.
Метод конфігурацій Розенброка заснований на пошуку мінімуму вздовж ліній розриву похідних і часто виявляється ефективним, коли інші методи не дозволяють отримати рішення. Його нерідко називають «методом обертання вісей координат», оскільки дослідження в околі вибраної точки ведеться саме таким методом. На відміну від попередніх методів, в яких вхідним змінним надають незалежні прирости, в методі Розенброка система координат повертається так, щоб одна з вісей була направлена вздовж лінії розриву похідних, положення якої визначається в результаті попереднього дослідження. Решта осей утворять з нею ортогональну систему координат. Метод Розенброка заснований на припущенні про унімодальність цільової функції і перевизначений для відшукання мінімуму функції багатьох змінних вигляду
(14.28)
при відсутності обмежень. На рис. 14.12 показана схема алгоритму, який використовується в цьому методі.
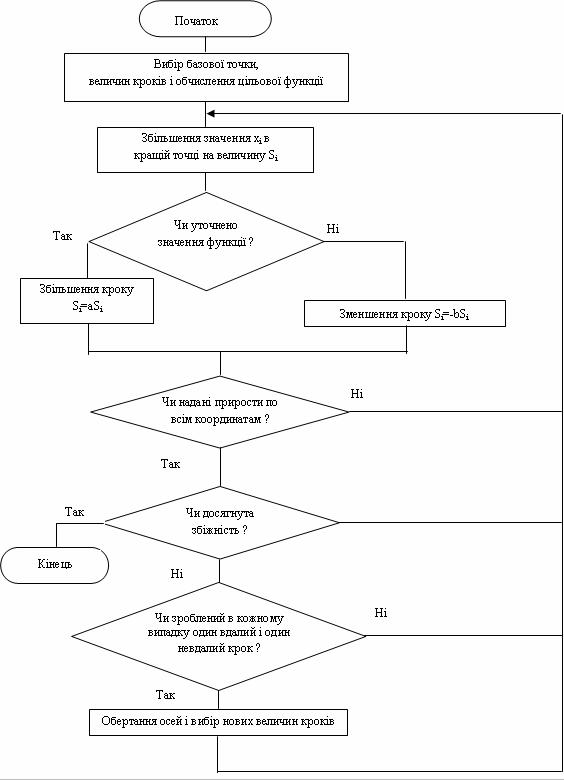
Виконується він наступним чином. Спочатку вибирають початкову точку, задають початкові величини кроків
і обчислюють цільову функцію. Після цього кожній змінній 
надають приріст
в напрямку, паралельному до відповідної осі координат в просторі проектування, і знову обчислюють цільову функцію
. Якщо її нове значення виявляється меншим за попереднє, то зсув вважається вдалим і наступний крок збільшується у відповідності з формулою
(14.29)
де 
. Якщо ж нове значення
виявляється більше за попереднє, то зсув вважається невдалим і наступний крок визначається по формулі
(14.30)
де
.
Здійснивши зсув по всім змінним, перевіряють збіжність і, якщо вона досягнута, пошук припиняють. В протилежному випадку вводять додаткову перевірку, щоб з'ясувати, чи були зроблені хоча б один успішний і однин безуспішний зсув в кожному напрямку. Якщо такого поєднання зсув не було, вся процедура повторюється, починаючи з першої змінної. Якщо ж подібне поєднання виявлене для кожного напрямку, осі повертають так, щоб вхідний напрямок пошуку співпав з найбільш перспективним з раніше розглянутих напрямків. Після цього вибирають нові значення кроків і продовжують пошук по всім змінним, користуючись новою системою координат.
На відміну від інших, даний алгоритм націлений на пошук оптимальної точки в кожному напрямку, а не просто на фіксований зсув по всім напрямкам. Величина кроку в процесі пошуку безупинно змінюється в залежності від конфігурації рельєфу поверхні. Поєднання обертання вектору, направленого вздовж лінії розриву похідних, з регулюванням масштабу робить метод Розенброка виключно ефективним при розв‘язанні складних задач оптимізації.
1. Щуп Т. Решение инженерных задач на ЭВМ. – М.: Мир, 1982. – 235с.
2. Бахвалов Н. С. Численные методы . Т. И. Анализ, алгебра, обычные диференциальные уравнения. – М.: Наука, 1975. – 631 с.
3. Ляшенко М.Я., Головань М.С. Чисельні методи: Підручник. Либідь. 1996. – 288 с.
4. Крылов В. И. и др. Численные методы . – М.: Наука, 1978. – 1979. – Т. 2. – 400 с.
5. Форсайт Дж., Малькольм., Моулер Р. Машинные методы математических вычислений. – М.: Мир, 1980. – 279c.
6. Д. Мэтьюз, Г. Цинк, Д. Куртис. Численне методы. Использование Matlab, –М. Издательский дом “Вильямс”, 2001. – 720 с. 720 с.
7. Гил Ф., Мюрей У. Численные методы условной оптимизации. – М.: Мир, 1977. – 290 с.
8. Василев Ф. П. Лекции по методам решения експериментальных задач. – М.: Изд – во Моск. Ун – то, 1984. – 374 с.
9. Полак Е. Численные методы оптимизации. – М. : Мир, 1974.
10. Пшеничний Б. Н., Данилин Ю. М. Численные методы в екстремальных задачах. – М. : Наука, 1975.
11. Моделирование и оптимизация на ЭВМ радиоэлектронных устройств / Под ред. З. М. Бенесона. – М. : Радио и связь, 1981. – 272 с.
12. И.В. Кузьмин, М.М. Биков, С.М. Москвина, А.И. Кузьмин. Методы оптимизации сложных систем. – Винница: ВДТУ, 2003. – 165с.
1. Що таке градієнт і антиградієнт? Поясніть математично.
2. В чому полягає сутність градієнтних методів пошуку оптимуму цільової функції.
3. Поясніть узагальнену математичну модель градієнтних методів пошуку оптимуму функції.
4. Покажіть, що функція 
є випуклою.
5. Знайдіть і класифікуйте стаціонарні точки функції 
.
6. Проведіть аналіз визначеності наступних квадратних форм:
