1.4 Комплексні показники надійності

Для відновлюваних ТЗ існує зацікавленість у вивченні послідовності випадкових подій, що являють собою повторюваність відмов, які виникають в результаті багаторазових відновлень.

Послідовність відмов називається потоком відмов.

Виділимо деякий інтервал часу від моменту включення t = 0 до деякого поточного значення часу t. Зробимо припущення, що на цьому інтервалі часу (0; t) виникло V_t відмов. Причому V_t – являє собою дискретну випадкову величину.

Позначимо через F_n(t) – ймовірність того, що на інтервалі (0; t) виникло не менше n відмов, тобто

(1.30)

З виразу (1.30) отримаємо формулу для визначення ймовірності появи n відмов на інтервалі (0; t)

(1.31)

1.4.1 Ведуча функція потоку відмов.

Найважливішою характеристикою потоку відмов є математичне сподівання кількості відмов на інтервалі (0; t). Ця характеристика називається ведучою функцією потоку відмов. Позначимо цю функцію через Н(t)

(1.32)

У зв’язку з тим, що після кожної відмови відбувається відновлення, то Н(t) являє собою також і середню кількість відновлень на інтервалі (0;t).

Середня кількість відмов в інтервалі часу (t₁; t₂) буде дорівнювати

(1.33)

За означенням середнього значення дискретної випадкової величини (математичного сподівання) маємо

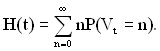(1.34)

Підставляючи вираз (1.31) у вираз (1.34) і розділивши суму на два доданки, отримаємо

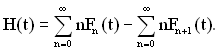(1.35)

В першій сумі виразу (1.35) член при n = 0 буде дорівнювати нулю і ним можна знехтувати. У другій сумі індекс підсумовування замінимо на m=n+1. Тоді вираз (1.35) набуде вигляду

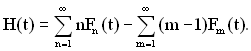(1.36)

Об’єднуючи суми рівняння (1.36), отримаємо кінцевий вираз для ведучої функції потоку відмов

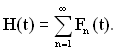(1.37)

1.4.2 Інтенсивність потоку відмов.

Тепер знайдемо середню кількість відмов на інтервалі (t₁; t₂), віднесену до тривалості цього інтервалу (t₁-t₂). Відповідно до виразу (1.33) це відношення буде дорівнювати

Межа такого відношення називається інтенсивністю потоку відмов і позначається через

. (1.38)

З виразів (1.38) і (1.37) випливає, що

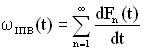. (1.39)

1.4.3 Функція розподілу потоку відмов.

Розглянемо зв'язок функції розподілу кількості відмов з показником безвідмовності та відновлюваності ТЗ, тобто з щільністю розподілу напрацювання до відмови та з щільністю розподілу часу відновлення.

При цьому існує два припущення:

1. Потік відмов і потік відновлень кожний окремо та разом являють собою послідовність незалежних подій;

2. На інтервалі відновлення відмови не виникають.

Через Т_k позначимо випадковий інтервал часу моменту виникнення k-ої відмови після першого ввімкнення ТЗ. В цьому випадку

, (1.40)

де – інтервал часу між відмовами, що складається з інтервалу відновлення та інтервалу безвідмовної роботи :

Т₀=; Т₁=.

Момент n-ої відмови буде дорівнювати сумі інтервалів між відмовами

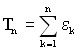. (1.41)

Подія, полягаюча в тому, що на інтервалі часу (0; t) з’явиться мінімум n відмов, еквівалентна події, при якій момент n-ої відмови передує моменту часу t.

Відповідно

,

або

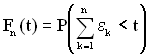. (1.42)

Оскільки випадкові величини незалежні, то визначення функції зводиться до задачі про розподіл суми скінченного числа незалежних величин. Як правило для вирішення подібних задач використовують метод характеристичних функцій.

Позначимо через – щільність розподілу випадкової величини . При цьому характеристичною функцією випадкової величини називається перетворення Фур’є її щільності розподілу, тобто

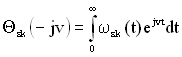. (1.43)

Щільність розподілу отримується із характеристичної функції шляхом зворотного перетворення Фур’є

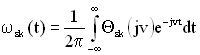. (1.44)

З виразу (1.43) випливає, що характеристична функція випадкової величини є середнє значення від . Але тоді для суми незалежних випадкових величин отримуємо:

,

,

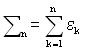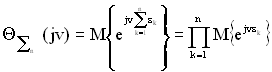або

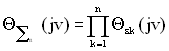. (1.45)

З рівняння (1.45) випливає, що характеристична функція суми незалежних випадкових величин дорівнює добутку характеристичних функцій доданків.

Щільність розподілу вказаної суми знаходиться оберненим перетворенням Фур’є

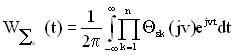. (1.46)

Оскільки і ці доданки незалежні, то

, (1.47)

де і – відповідно характеристичні функції відновлення та безвідмовної роботи.

Розраховуючи ці функції за допомогою перетворення Фур’є від щільності розподілу часу відновлення і щільності розподілу напрацювання до відмови :

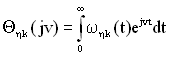, (1.48)

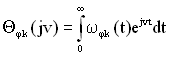. (1.49)

Об’єднуючи вирази (1.42), (1.44), (1.46) - (1.49) отримаємо шукану залежність функції F_n(t) від характеристики відновлення і безвідмовності

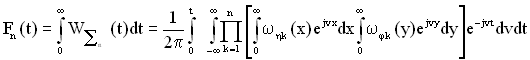. (1.50)

У випадку однорідних потоків відмов і потоків відновлень функції розподілу та не залежать від номеру інтервалу. Тому в рівнянні (1.50) добуток можна замінити n-ою степеню виразу, поміщеному в квадратні дужки, тобто

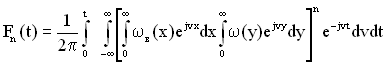. (1.51)

Якщо відновлення відбувається миттєво, то =, і відповідно рівняння (1.51) набуває вигляду

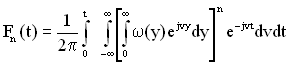. (1.52)