1.5 Показники довговічності та збережності
Календарний термін від початку експлуатації ТЗ до переходу в граничний стан називають терміном роботи ТЗ. Якщо термін роботи ТЗ – це випадкова величина (позначимо її tр), то показник довговічності може визначатися як середній термін роботи (математичне сподівання Тср)
![]() , (1.53)
, (1.53)
або гама-відсотковий термін роботи ![]() , що визначається співвідношенням
, що визначається співвідношенням
![]() . (1.54)
. (1.54)
Таким чином, ![]() – це календарний термін від початку експлуатації ТЗ, протягом якого ТЗ не досягне граничного стану із заданою ймовірністю
γ (вираженою у відсотках).
– це календарний термін від початку експлуатації ТЗ, протягом якого ТЗ не досягне граничного стану із заданою ймовірністю
γ (вираженою у відсотках).
Як показник довговічності можна використати також і ресурс ТЗ.
Ресурсом ТЗ називають напрацювання засобу до граничного стану, при досягненні якого подальша експлуатація припиняється. При цьому довговічність ТЗ зазвичай характеризують напрацюванням засобу, протягом якого він не досягне граничного стану із заданою ймовірністю γ.
Таке напрацювання називають гама-відсотковим ресурсом. Для визначення цього ресурсу потрібно знати функцію розподілу ресурсу.
Терміном збережності називається період зберігання засобу в певних умовах, протягом якого зберігаються початкові показники його якості.
Інколи збережність характеризують період зберігання, протягом якого ТЗ зберігає встановлені показники із заданою ймовірністю γ.
Такий період зберігання називається гама-відсотковим терміном збережності. Для його визначення потрібно знати функцію розподілу терміну збережності.
1.6 Структурна надійність технічних засобів
Структурною надійністю ТЗ називається результуюча надійність при заданій структурі і відомих значеннях надійності всіх блоків і елементів, що входять до складу ТЗ. Розподіл ТЗ на блоки і елементи здійснюється на базі єдності функціонування і фізичних процесів, що відбуваються при його роботі.
Якщо відмова ТЗ настає при відмові одного з його елементів, то такий ТЗ має основне з'єднання елементів. При розрахунку надійності таких ТЗ відмова елемента є подією випадковою і незалежною, а ймовірність безвідмовної роботи ТЗ протягом часу t дорівнює добуткові ймовірностей його елементів протягом того ж часу:
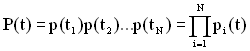 , (1.55)
, (1.55)
або
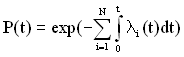 . (1.56)
. (1.56)
При експоненційному законі розподілу відмов, тобто для нормального (звичайного) періоду роботи ТЗ:
![]() ,
, ![]() ,
, ![]() ,
, 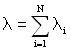 , (1.57)
, (1.57)
де ![]() – інтенсивність відмов
– інтенсивність відмов ![]() -го елемента.
-го елемента.
При розрахунку високонадійних ТЗ з достатньою для практики точністю можна користуватися наближеними формулами:
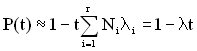 ,
, 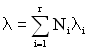 ,
, ![]()
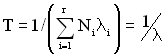 ,
, ![]() , (1.58)
, (1.58)
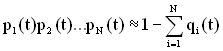 ,
, ![]() ,
, ![]() , (1.59)
, (1.59)
де ![]() – число типів елементів;
– число типів елементів;
![]() – ймовірність відмов
– ймовірність відмов ![]() -го елемента.
-го елемента.
Одним з методів підвищення надійності є резервування (backuping). Резервованим з'єднанням ТЗ називається таке з'єднання, при якому відмова настає тільки після відмови основного блоку чи елементів і всіх резервних блоків і елементів.
Основним параметром резервування є його кратність m, тобто відношення кількості резервних елементів до кількості основних елементів. Розрізняють резервування з цілою і дробовою кратністю. При резервуванні з цілою кратністю величина m – ціле число, а при резервуванні з дробовою кратністю m – дробове число.
За способом ввімкнення резервування поділяється на постійне і резервування заміщенням. Постійне резервування (permanent backuping) – резервування, при якому резервні елементи підключені до основних протягом усього часу роботи і знаходяться в однаковому з ними режимі. Резервування заміщенням (backuping a substitution) – резервування, при якому резервні елементи заміщають основні після їхньої відмови.
При включенні резерву за способом заміщення резервні елементи до моменту включення в роботу можуть знаходитися в трьох станах:
– навантаженому резерві;
– полегшеному резерві;
– ненавантаженому резерві.
Якщо елементи резервних блоків мають відмови типу «обрив» або «коротке замикання», то ймовірність безвідмовної роботи потрібно обчислювати, підсумовуючи ймовірності всіх сприятливих (не призводячих до відмови) гіпотез:
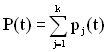 , (1.60)
, (1.60)
де ![]() – ймовірність j-ої сприятливої гіпотези, обчисленої з врахуванням двох видів відмов;
– ймовірність j-ої сприятливої гіпотези, обчисленої з врахуванням двох видів відмов;
![]() – кількість сприятливих гіпотез.
– кількість сприятливих гіпотез.
Для елементів складної системи справедливі вирази:
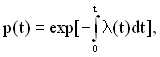
![]() =1, (1.61)
=1, (1.61)
де λ(t) – інтенсивність відмов елемента;
![]()
![]() – ймовірність виникнення «обриву» і «короткого замикання» відповідно.
– ймовірність виникнення «обриву» і «короткого замикання» відповідно.
При експоненційному законі розподілу відмов справедливі вирази:
![]()
![]() ,
, ![]() , (1.62)
, (1.62)
де ![]()
![]() – інтенсивність відмов елемента за «обривом» та «коротким замиканням».
– інтенсивність відмов елемента за «обривом» та «коротким замиканням».
1.7 Оцінка показників надійності за статистичною інформацією про відмови при експлуатації та випробуваннях
При оцінюванні показників надійності ТЗ за статистичною інформацією про відмови при експлуатації визначається закон розподілу (distributing law) відмов і його параметри. За знайденим законом розраховується будь-яка характеристика надійності ТЗ.
Методика визначення закону розподілу містить у собі такі етапи: підготовка отриманих даних, побудова гістограми та перевірка відповідності закону розподілу з використанням одного з критеріїв згоди (Колмогорова, Пірсона, Стьюдента, Фішера чи ін.).
Етап I. Отримана інформація систематизується в порядку зростання часу спостереження, що розбивається на однакові інтервали часу (табл. 1.1).
Таблиця 1.1 – Вихідні дані для визначення закону розподілу відмов

Етап II. За даними табл. 1.1 будується гістограма необхідного показника надійності та апроксимується кривою, за виглядом якої орієнтовно установлюється закон розподілу відмов шляхом порівняння із відповідними теоретичними кривими (рис. 1.2).
Етап III. Перевірка відповідності прийнятого закону розподілу відмов здійснюється за критеріями згоди, найбільш поширеними є критерії Пірсона і Колмогорова.
За критерієм Пірсона обчислюють ймовірність вигляду:
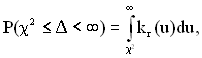 (1.63)
(1.63)
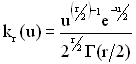 , (1.64)
, (1.64)
де ![]() – кількість ступенів вільності розподілу;
– кількість ступенів вільності розподілу;
∆ – міра розбіжності;
![]() – функція щільності розподілу:
– функція щільності розподілу:
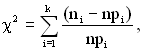 (1.65)
(1.65)
де ![]() – загальна кількість ТЗ, що випробовується;
– загальна кількість ТЗ, що випробовується;
![]() – частота
– частота ![]() -го інтервалу статистичного ряду;
-го інтервалу статистичного ряду;
![]() – число інтервалів статистичного ряду.
– число інтервалів статистичного ряду.
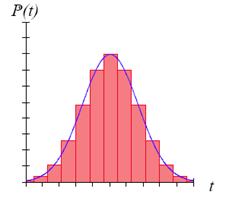
Рисунок 1.2 – Експериментальна гістограма показника надійності
Якщо ймовірність ![]() , то експериментальний розподіл відповідає теоретичному.
, то експериментальний розподіл відповідає теоретичному.
За критерієм Колмогорова відповідність теоретичного і експериментального розподілів перевіряється виконанням умови
![]() , (1.66)
, (1.66)
де ![]() – найбільше відхилення теоретичної кривої розподілу від експериментальної;
– найбільше відхилення теоретичної кривої розподілу від експериментальної;
![]() – загальна кількість експериментальних точок.
– загальна кількість експериментальних точок.
Приклад 1.7. У результаті досвіду отримано такий варіаційний ряд
часу справної роботи в годинах:
2; 3; 3; 5; 6; 7; 8; 8; 9; 9; 13; 15; 16; 17; 18; 20; 21; 25; 28; 35; 37; 53; 56; 69; 77; 86; 98; 119.
Потрібно встановити закон розподілу часу безвідмовної роботи.
Розв’язування:
Загальна кількість відмов ![]() .
.
Заповнюємо табл. 1.2 за формою табл. 1.1.
Таблиця 1.2 – Статистичні дані про відмови
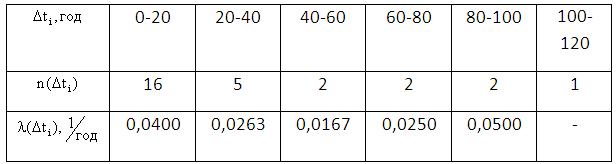
Будуємо гістограму λ(∆t), що подана на рис. 1.3.
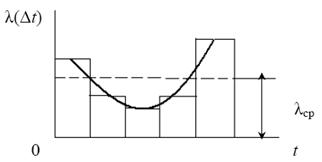
Рисунок 1.3 – Гістограма статистичних даних про відмови
Знаходимо середнє значення ![]() і найбільше відхилення
і найбільше відхилення ![]() :
:
![]() ,
,
![]() .
.
Перевіряємо експериментальний розподіл на відповідність запропонованому експонентному розподілові за критерієм згоди Колмогорова (1.66):
![]() .
.
Відповідно до критерію вважаємо, що закон розподілу відмов експоненційний.
У результаті досліджень одержують точкові та інтервальні оцінки (довірчі інтервали). При інтервальних оцінках визначається, який інтервал оцінок із заданою довірчою ймовірністю α накриває математичне очікування параметра θ, що оцінюється
![]() , (1.67)
, (1.67)
де ![]()
![]() – нижня і верхня довірчі межі параметра
– нижня і верхня довірчі межі параметра ![]() .
.
Ймовірність того, що значення ![]() вийде з інтервалу [
вийде з інтервалу [![]()
![]() ], називають рівнем значущості
β
], називають рівнем значущості
β
![]() . (1.68)
. (1.68)
Часто встановлюють одну з меж інтервалу: нижню або верхню з довірчими ймовірностями ![]() або
або ![]() , відповідно (односторонній довірчий інтервал):
, відповідно (односторонній довірчий інтервал):
![]() , (1.69)
, (1.69)
![]() , (1.70)
, (1.70)
![]() . (1.71)
. (1.71)
Для різних законів розподілу відмов складають різні плани випробувань. При проведенні випробувань найбільш часто застосовуються такі закони розподілу: експоненційний, нормальний, біноміальний і гама-розподіл. Оцінки показників надійності розраховуються за формулами, наведеними у табл. 1.3 для різних законів розподілу відповідно до планів випробувань, що позначаються за допомогою трьох букв:
Плани випробувань та інтервальні оцінки показників надійності згідно з цими планами наведені в табл. 1.3.
Таблиця 1.3 – Плани випробувань та інтервальні оцінки
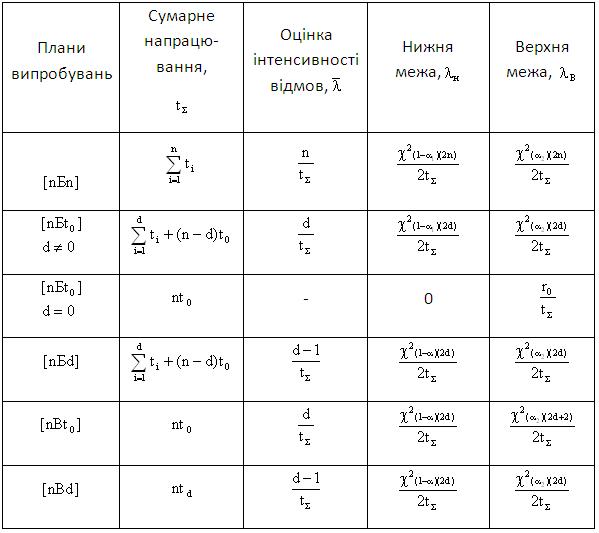
Плани, що закінчуються при відмові всіх зразків вибірки, позначаються буквою ![]() ; плани, що закінчуються через заданий час, позначаються буквою
; плани, що закінчуються через заданий час, позначаються буквою ![]() ; плани, що закінчуються після появи встановленої кількості відмов, позначаються буквою
; плани, що закінчуються після появи встановленої кількості відмов, позначаються буквою ![]() ;
; ![]() – час від початку випробувань до
– час від початку випробувань до ![]() -ої відмови;
-ої відмови; ![]() – сумарне напрацювання.
– сумарне напрацювання.
Значення квантилів ![]() розподілів вибираються з довідникових таблиць залежно від заданої довірчої ймовірності та числа ступенів вільності. Значення коефіцієнта
розподілів вибираються з довідникових таблиць залежно від заданої довірчої ймовірності та числа ступенів вільності. Значення коефіцієнта ![]() для довірчої ймовірності
для довірчої ймовірності ![]() = 0.8
= 0.8 ![]() 0.999 наведені в табл. 1.4.
0.999 наведені в табл. 1.4.
Таблиця 1.4 – Значення коефіцієнта ![]()

Експоненційний розподіл використовується для оцінки раптових відмов. Інтервальні оцінки показників безвідмовності розраховуються за формулами:
![]() , (1.72)
, (1.72)
![]() , (1.73)
, (1.73)
![]() ;
; ![]() . (1.74)
. (1.74)
Нормальний закон розподілу відмов використовується для оцінки поступових відмов. Щільність нормального розподілу для випадкової величини ![]() в інтервалі [–∞; +∞] дорівнює
в інтервалі [–∞; +∞] дорівнює
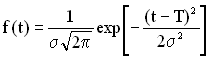 . (1.75)
. (1.75)
Оскільки випадкова величина ![]() лежить в інтервалі [0; +∞], то для оцінки показників надійності береться усічений нормальний розподіл із щільністю розподілу
лежить в інтервалі [0; +∞], то для оцінки показників надійності береться усічений нормальний розподіл із щільністю розподілу
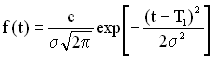 , (1.76)
, (1.76)
де ![]() – нормувальний множник, що визначається з виразу:
– нормувальний множник, що визначається з виразу:
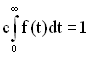 , (1.77)
, (1.77)
![]()
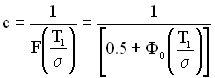 , (1.78)
, (1.78)
де 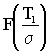 – інтегральна функція нормального розподілу;
– інтегральна функція нормального розподілу;
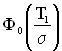 – центрована і нормована функція Лапласа.
– центрована і нормована функція Лапласа.
Середнє напрацювання до відмови і параметр ![]() усіченого нормального перерозподілу пов'язані залежністю
усіченого нормального перерозподілу пов'язані залежністю
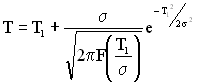 . (1.79)
. (1.79)
При випробуванні вибірки об’ємом в ![]() виробів з напрацюванням
виробів з напрацюванням ![]() параметри розподілу
параметри розподілу ![]() та
та ![]() оцінюються за формулами:
оцінюються за формулами:
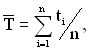 (1.80)
(1.80)
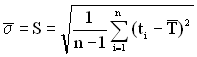 , (1.81)
, (1.81)
![]() , (1.82)
, (1.82)
![]() , (1.83)
, (1.83)
де ![]() – квантиль розподілу Стьюдента для ймовірності
α або рівня значимості
– квантиль розподілу Стьюдента для ймовірності
α або рівня значимості ![]() і числа ступенів вільності
і числа ступенів вільності ![]() .
.
Нижня та верхня межі СКВ визначаються з виразів:
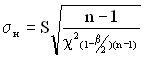 , (1.84)
, (1.84)
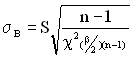 , (1.85)
, (1.85)
де ![]() – квантиль Хі-квадрат розподілу при ймовірності
– квантиль Хі-квадрат розподілу при ймовірності ![]() і числі ступенів вільності:
і числі ступенів вільності: ![]() ;
;
![]() – те ж для ймовірності
– те ж для ймовірності ![]() .
.
Якщо час безвідмовної роботи ТЗ має нормальний розподіл, то оцінка ймовірності безвідмовної роботи за час ![]() визначається за формулою
визначається за формулою
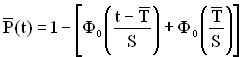 , (1.86)
, (1.86)
де ![]() – центрована і нормована функція Лапласа.
– центрована і нормована функція Лапласа.
Оскільки функція ![]() непарна, тобто , те
непарна, тобто , те ![]()
![]() , то
, то
![]() , (1.87)
, (1.87)
де ![]() – квантиль нормального розподілу (при
– квантиль нормального розподілу (при ![]() і
і ![]() );
);
![]() – оцінка стандартного відхилення
– оцінка стандартного відхилення ![]() :
:
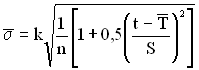 , (1.88)
, (1.88)
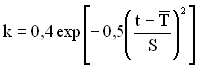 . (1.89)
. (1.89)
Якщо при випробуваннях не реєструється напрацювання ТЗ, а реєструються тільки відмови, то оцінки ймовірності безвідмовної роботи та ймовірності відмови будуть визначатись за формулами:
![]()
![]() , (1.90)
, (1.90)
де ![]() і
і ![]() – оцінки ймовірності безвідмовної роботи та ймовірності відмов, відповідно;
– оцінки ймовірності безвідмовної роботи та ймовірності відмов, відповідно;
![]() – об’єм вибірки;
– об’єм вибірки;
![]() – кількість зареєстрованих відмов.
– кількість зареєстрованих відмов.
Довірчі межі ймовірності відмови визначаються за формулами:
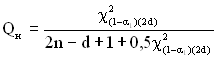 , (1.91)
, (1.91)
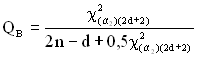 , (1.92)
, (1.92)
де ![]() – квантиль Хі-квадрат розподілу з
– квантиль Хі-квадрат розподілу з ![]() ступенями вільності для ймовірності
ступенями вільності для ймовірності ![]() ;
;
![]() – квантиль Хі-квадрат розподілу з
– квантиль Хі-квадрат розподілу з ![]() ступенями вільності для ймовірності
ступенями вільності для ймовірності ![]() .
.
Якщо число відмов ![]() , то
, то
![]() ,
, ![]() ,
, ![]() . (1.93)
. (1.93)
Об’єм вибірки ![]() при проведенні випробувань для оцінки
при проведенні випробувань для оцінки ![]() з абсолютною похибкою
з абсолютною похибкою ![]() при довірчій ймовірності
при довірчій ймовірності ![]() розраховується за рівнянням
розраховується за рівнянням
![]() , (1.94)
, (1.94)
де ![]() – квантиль нормального розподілу для
– квантиль нормального розподілу для ![]() ;
;
![]() – орієнтовне значення ймовірності відмови.
– орієнтовне значення ймовірності відмови.