7.7 Цифрова фільтрація сигналів

 

Терміном цифровий фільтр називають апаратну або програмну реалізацію математичного алгоритму, входом якого є цифровий сигнал, а виходом – інший цифровий сигнал, форма якого і/або амплітудна та фазова характеристики спеціальним чином модифіковані.

В аналогових системах під фільтром розуміють деякий лінійний пристрій зі специальною частотною характеристикою , яке перетворює вхідний сигнал у вихідний (рис. 7.8), придушуючи або, навпаки, підсилюючи при цьому певні частоти в спектрі вхідного сигналу. Вихідний сигнал знаходиться як згортка вхідного сигналу і імпульсної характеристики фільтра :

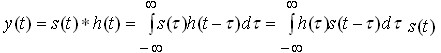
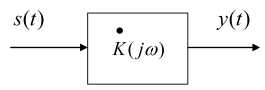
Рисунок 1.8 – Цифровий фільтр

 

За аналогією з аналоговим фільтром, цифровий фільтр (ЦФ, digital filter) перетворює послідовність відліків вхідного сигналу у числову послідовність вихідного сигналу . Для ЦФ також вводять поняття імпульсної характеристики , що є реакцією ЦФ на «одиничний імпульс (скачок)» тобто

Імпульсну характеристику (pulse response characteristic) ЦФ можна трактувати як результат дискретизації безперервної імпульсної характеристики відповідного аналогового фільтра- прототипу (рис. 1.9).

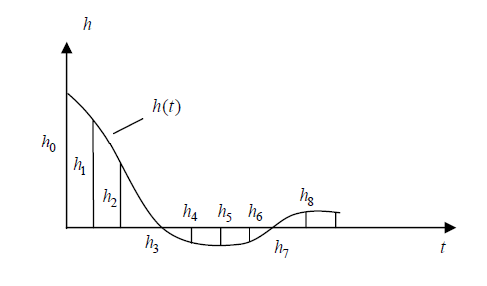
Рисунок 1.9 – Дискретизація імпульсної характеристики

 

Якщо взяти кінцеве число відліків , тоді отримаємо ЦФ із кінцево-імпульсною характеристикою (КІХ-фільтр, finite impulse response filtering). Якщо взяти нескінченне число відліків , отримаємо ЦФ із безкінечно-імпульсною характеристикою (БІХ-фільтр, infinite impulse response filtering).

Під фільтром зазвичай розуміють систему, що одні частоти пропускає, а інші затримує. Однак у техніці цифрової обробки сигналів поняття фільтра трактується більш широко. Дискретним фільтром називають довільну систему обробки дискретного сигналу, що має властивості лінійності й стаціонарності. Існують також фільтри зі змінними параметрами, наприклад, адаптивні фільтри, що змінюють свої параметри залежно від статистичних властивостей вхідного сигналу.

У загальному випадку, фільтр змінює в спектрі сигналу і амплітуди гармонік, і їх фази. Однак фільтри можна проектувати так, щоб вони не змінювали фазу сигналу. Такі фільтри називаються фільтрами з лінійною фазою. Це означає, що якщо вони і змінюють фазу сигналу, то роблять це так, що всі гармоніки сигналу зсуваються за часом на одну й ту ж величину. Таким чином, фільтри з лінійною фазою не спотворюють фазу сигналу, а лише зсувають весь сигнал в часі. Ядро згортки такого фільтра симетричне щодо своєї центральної точки.

Основна властивість будь-якого фільтру – це його частотна і фазова характеристики. Вони показують, як фільтр впливає на амплітуду і фазу різних гармонік оброблюваного сигналу. Якщо фільтр має лінійну фазу, то розглядається лише частотна характеристика фільтру. Зазвичай частотна характеристика зображується у вигляді графіка залежності амплітуди від частоти (в децибелах). Наприклад, якщо фільтр пропускає всі сигнали в смузі 0 ... 10 кГц без зміни, а всі сигнали в смузі вище 10 кГц подавляє в 2 рази (на 6 дБ), то частотна характеристика буде мати такий вигляд:

.

Частотна характеристика в 0 дБ показує, що дані частоти фільтр пропускає без зміни. Ті частоти, амплітуда яких послаблюється фільтром в 2 рази, повинні мати амплітуду на 6 дБ менше. Тому їх амплітуда становить -6 дБ. Якщо фільтр посилює частоти, то його частотна характеристика на цих частотах є позитивною.

Вихідний сигнал y(k) фільтра, що має нетривіальну частотну характеристикою, залежить від декількох відліків вхідного сигналу x(k). У загальному випадку при обчисленні вихідного відліку використовується також деяка кількість попередніх відліків вихідного сигналу. Для фільтрів, що не використовують вихідні відліки, рівняння фільтрації має вигляд

Такі фільтри називаються не рекурсивними (nonrecursive filter) або трансверсальними. Кількість відліків m називається порядком фільтра. Структурна схема нерекурсивного фільтра показана на рис.1.10. Імпульсна характеристика нерекурсивного фільтра визначається його коефіцієнтами h(k) = bk. Так як в реальному пристрої кількість ліній затримки обмежено, а отже, і кількість коефіцієнтів, нерекурсивні фільтри відносять до класу КІХ-фільтрів.

Рисунок 1.10 – Нерекурсивний фільтр

 

Фільтр, у якому також використовуються і вихідні відліки, називається рекурсивним (recursive filter) (рис.1.11). Рівняння рекурсивного фільтра має вигляд

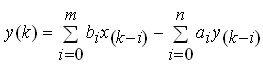
Наявність у схемі рекурсивного фільтра зворотних зв'язків дозволяє одержати безкінченну імпульсну характеристику, тому такі фільтри належать до класу БІХ-фільтрів. Проте такі фільтри при деяких умовах можуть бути нестійкими.

Під проектуванням (синтезом) цифрового фільтра розуміють вибір таких наборів його коефіцієнтів {ai} і {bi}, які задовольняють заданим вимогам. У завдання проектування входить також і вибір потрібної структури фільтра з урахуванням необхідної точності обчислень.

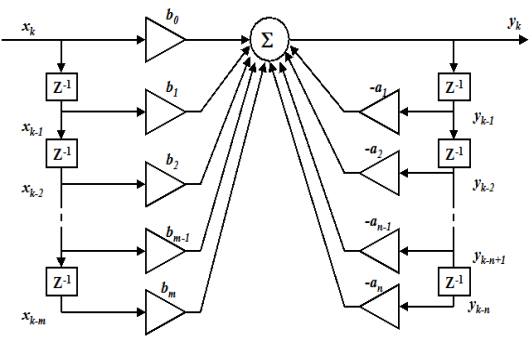
Рисунок 1.11 – Рекурсивний фільтр

 

У проектуванні та реалізації цифрових фільтрів застосовується безліч різноманітних підходів і методів, вибір яких залежить від багатьох факторів, зокрема – від того, як формулюється завдання фільтрації.

Найчастіше цифрова фільтрація застосовується для виділення сигналу або для відновлення сигналу. Виділення "корисного" сигналу необхідно, коли сигнал, що надходить у систему із зовнішнього середовища, змішаний із шумами, викликаними різноманітними фізичними процесами, що мають, як правило, випадковий характер. Відновлення сигналу необхідно через можливі спотворення сигналу, викликані роботою апаратури.

У зв'язку з тим, що теорія апроксимації ідеальних АЧХ аналоговими засобами добре розвинена, широке поширення одержали методи синтезу цифрових фільтрів по аналогових прототипах.

У прямих методах синтезу без використання аналогових прототипів часто використовується той факт, що ДПФ можна трактувати як обробку сигналу фільтром з відповідною імпульсною характеристикою.

Оскільки ДПФ лінійної згортки дорівнює добутку ДПФ послідовностей, що звертаються, алгоритм фільтрації в частотній області полягає в наступному:

  •  Послідовність відліків вхідного сигналу та імпульсна характеристика фільтра доповнюються нулями так, щоб довжини послідовностей стали рівними і не меншими, ніж сума довжин вихідних послідовностей мінус одиниця.
  •  Обчислюються ДПФ доповнених нулями послідовностей.
  •  Обчислені ДПФ поелементно перемножуються
  •  Обчислюється обернене ДПФ від результату перемножування.

    Для підвищення ефективності фільтрація здійснюється в частотній області з використанням ШПФ.

    При проектуванні цифрових фільтрів один із ключових моментів пов'язаний з особливостями технічної реалізації і рядом обмежень, обумовлених розрядністю цифрових обчислювальних пристроїв:

  •  шум квантування, що виникає при аналого-цифровому перетворенні;
  •  спотворення характеристик, що відбуваються при квантуванні коефіцієнтів цифрових фільтрів;
  •  переповнення розрядної сітки в процесі обчислень;
  •  округлення проміжних результатів обчислень.

    Тому при проектуванні цифрових фільтрів важливо правильно вибрати способи й формати подання чисел (дійсні або комплексні числа, з фіксованою або плаваючою крапкою тощо), динамічний діапазон подання даних, обумовлений розрядністю регістрів устаткування, а також оцінити можливий вплив шумів і спотворень.

     

    Контрольні завдання та запитання

    1. Які перетворення мають місце при цифровій обробці сигналів?

    2.  Що таке дискретний сигнал і дискретна послідовність?

    3. У чому полягають взаємозв'язок і відмінність спектрів дискретного та аналогового сигналів?

    4. Як по відомому спектрі аналогового сигналу визначити спектр відповідного йому дискретного сигналу?

    5. У чому полягає явище накладення спектрів при дискретизації сигналів?

    6.  Як здійснюється цифрове кодування сигналу?

    7.  Як визначається автокореляційна функція і спектральна щільність шуму квантування АЦП?

    8. Відомо, що для отримання розбірливої людської мови її достаньо дискретизувати з частотою 8 кГц. Який діапазон частот може бути правильно передано такий цифровим записом? Що необхідно зробити у разі дискретизації для правильної передачі цього діапазону?

    9. Сигнал х[n], відмінний від нуля на відрізку [А,В], згортається з сигналом h[n], відмінним від нуля на відрізку [С,D]. Знайти відрізок, на якому може бути відмінний від нуля результуючий сигнал.

    10. Розрахувати, скільки множень потрібно зробити для обчислення згортки сигналу довжини N з ядром довжини М.

    11. Частота дискретизації сигналу дорівнює 44100 Гц. Розмір ШПФ дорівнює 4096. Яка довжина аналізованого блоку в секундах? За якими частотами (у герцах) буде розкладений сигнал?

    12. Яку частотну роздільну здатність спектра ми отримаємо в попередньому прикладі? Який розмір ШПФ потрібно використовувати, щоб отримати частотну роздільну здатність близько 4 Гц?

    13. Реалізувати знаходження і відображення спектру заданої ділянки сигналу. Ввести можливість вибору довжини сигналу, розміру ШПФ, виду вагового вікна.

    14. Реалізувати швидку згортку двох сигналів через частотну область.

    15. Реалізувати секційну згортку двох сигналів через частотну область.

    16. Реалізувати алгоритм проектування фільтра за заданою частотною характеристикою. Спроектувати НЧ-фільтр з довільними параметрами.

    17. Показати аналітично, що обернене ДПФ можна виконати за допомогою співвідношення (1.12).

    18. Виконати чисельно ДПФ по формулах (1.7), (1.8), (1.12) і зрівняти відновлені сигнали. Розрахувати їх АЧХ і ФЧХ.

    19.  Обчислити обернене ДПФ відповідно до (1.13), використовуючи тільки інформацію про ФЧХ сигналу.

    20. Чим відрізняється рекурсивний фільтр від нерекурсивного? Опишіть рівняння для обох фільтрів.

    21. У чому полягає завдання проектування цифрових фільтрів? Які підходи при цьому використовуються?

    22.  Як виглядає алгоритм фільтрації із застосуванням ДПФ?

    23. Які технічні обмеження впливають на характеристики проектованих фільтрів?