
9.2. Інтервальне розширення та звуження
Подання будь-якої загальної функції gR в вигляді інтервальної функції gIR, є одною з найважливіших проблем інтервального аналізу.
Інтервальним розширенням функції gR(х), х ? R, назвемо такий елемент gIR(Х), ХÎІR, що при х Î Х виконується умова gR(х)Î gIR(Х).
Інтервальне розширення позначається як:
![]() . (3.7)
. (3.7)
З точки зору практичного застосування інтервальних методів буває доцільним визначати інтервальне розширення більш спеціально, а саме, задаючи засіб його отримання. Підтвердженням сказаного можуть служити наступні приклади:
Функція gIR(Х), що отримана заміною дійсного аргументу х в раціональній функції gR(х) інтервальним аргументом Х з переходом в інтервальну арифметику,називається природним інтервальним розширенням. В цьому випадку справедлива наступна теорема.
Теорема 3.1. Якщо gIR(Х) - природне інтервальне розширення gR(х) і кожна компонента вектору Х= (Х1,..., Хn) в gIR(Х) зустрічається не більш одного разу, то
gIR(Х) = ![]() .
.
Як видно, в цьому випадку для знаходження області значень gR(х) при х ![]() Х достатньо обчислювати раціональний інтервальний вираз gIR(Х), тоді як, оперуючи дійсними функціями, ми повинні визначити нескінченну множину {gR(х) | х
Х достатньо обчислювати раціональний інтервальний вираз gIR(Х), тоді як, оперуючи дійсними функціями, ми повинні визначити нескінченну множину {gR(х) | х ![]() Х}.
Х}.
б) Якщо множину дійсних чисел R прирівняти до множини машинних чисел Rм, то тоді інтервальне розширення функції gR(x) буде мати вигляд
gIR(Х)=(gR(x))М+[-![]() ],
],
де (gR(x))М – результат обчислення gR(x) на машині, а ?(х) - абсолютна похибка gR(x), що дозволяє враховувати помилки машинного обчислення. При цьому ?(х) оцінюється величиною ?0|(gR(x))М|, де ?0-мінімальне машинне число.
Шляхом оператора Di можна перейти до дій над інтервалами. Необхідність в подібному інтервальному розширенні може виникнути наприклад, при врахуванні помилок подання на ЕОМ констант, що входять в функцію gR(x).
Потрібно зауважити, що з gR = ?Rне слідує Di gR = Di ?R. Приведемо наочний приклад.
Нехай gR(x) = ![]() ?R=(
?R=(![]() ), X0=< 1, 4 >. Для відповідних природних інтервальних розширень gIR(Х) =
), X0=< 1, 4 >. Для відповідних природних інтервальних розширень gIR(Х) = ![]() та ?IR(Х) = =(
та ?IR(Х) = =(![]() ) маємоgIR(Х)=<0 , 7>, ?IR(Х) = < -7/2, 21>.
) маємоgIR(Х)=<0 , 7>, ?IR(Х) = < -7/2, 21>.
Зворотною операцією щодо інтервального розширення є інтервальне звуження.
Інтервальним звуженням функції F(X), X?IR, називають відображення f (x), x?IR, що отримується з F(X), при X=[x, x]=x. В символьному запису:
![]() . (3.8)
. (3.8)
Потрібно звернути увагу на деякі аспекти. Наприклад, розглянемо звуження функції gIR(Х) по X.
З класу еквівалентності ![]() завжди можна виділити відображення, інтервальне розширення яких включають gIR(X). Для цього до
завжди можна виділити відображення, інтервальне розширення яких включають gIR(X). Для цього до ![]() достатньо додати деяке відображення ?(х), таке що:
достатньо додати деяке відображення ?(х), таке що:
![]() але
але ![]()
Наприклад, ?R(x)=x-x. З іншого боку розширення gIR(X) може бути таке, що з відповідного класу еквівалентності можна виділити відображення, інтервальні розширення яких можуть як включати, так і включатися в gIR(X).
Справді, нехай, наприклад, gIR(X)=Х2-5Х. Тоді ![]() . Розглянемо два елементи з класу еквівалентності gR(х) = х2-5х, а саме
. Розглянемо два елементи з класу еквівалентності gR(х) = х2-5х, а саме ![]() та
та ![]() Для відповідних природних інтервальних розширень в точці Х0 = <2, 4> маємо
Для відповідних природних інтервальних розширень в точці Х0 = <2, 4> маємо ![]() =<-12, -2>,
=<-12, -2>, ![]() = <-18, 8>, в той час як
= <-18, 8>, в той час як ![]() = <-16, 6>, тобто
= <-16, 6>, тобто ![]() .
.
Застосування інтервальних засобів припускає побудову інтервальних розширень, на які накладаються умови найбільшої звуженості. В теоремі 3.1 наведена достатня умова найбільшої звуженості для випадку раціональних функцій.
9.3 Диференціювання та інтегрування в інтервальному аналізі
Підхід до диференціювання та інтегрування функції в інтервальній математиці не суттєво, але відрізняється від звичайної математики. Але останні дослідження вчених математиків наблизили ці процеси до того, що нам відомо з дійсної математики.
Одним з перших способів розрахунку похідної від інтервальної функції базувався на так званих методах занурення. Але застосування цього способу на практиці виявилось не дуже зручним.Тому дослідники спрямовували свій пошук на більш практичні способи диференціювання. В наш час найбільш поширеним є підхід до диференціювання, який ввели болгарські вчені. Вони відповідно до дійсної математики дещо змінили підхід до визначення послідовності, та визначили поняття збіжності послідовності, знаходження границі послідовності в інтервальній математиці. Після визначення границі послідовності стало можливим сформулювати поняття диференціального обчислення для інтервальних функції. Отримане визначення стало дуже схожим на те, що ми звикли чути в математиці дійсних чисел.
Припустимо, що задана послідовність інтервалів {Аn}, Аn![]() IR. Назвемо інтервал А, який є перетином всіх інтервалів, які включають в себе всі або майже всі, за винятком обмеженої кількості, інтервали послідовності {Аn}, s – границею послідовності
IR. Назвемо інтервал А, який є перетином всіх інтервалів, які включають в себе всі або майже всі, за винятком обмеженої кількості, інтервали послідовності {Аn}, s – границею послідовності ![]() :
:
![]() . (3.9)
. (3.9)
Якщо ![]() – послідовність дійсних чисел, то
– послідовність дійсних чисел, то ![]() – це мінімальний інтервал, який включає всі граничні точки послідовності. Наприклад:
– це мінімальний інтервал, який включає всі граничні точки послідовності. Наприклад: ![]() Відповідно до поняття границі послідовності вводиться поняття границі інтервальної функції.
Відповідно до поняття границі послідовності вводиться поняття границі інтервальної функції.
Припустимо, що ![]() . Будемо називати інтервал А s-границею функції в точці х0, якщо А є перетином всіх інтервалів, які включають в себе інтервали виду
. Будемо називати інтервал А s-границею функції в точці х0, якщо А є перетином всіх інтервалів, які включають в себе інтервали виду
![]() (3.10)
(3.10)
де ![]() .
.
Введемо визначення границі інтервальної функції G, заданої через дійсні граничні функції: ![]() Нехай G – інтервальна функція, визначена в виколотому околі точки
Нехай G – інтервальна функція, визначена в виколотому околі точки ![]() . Назвемо s-границею функції G при
. Назвемо s-границею функції G при ![]() інтервал
інтервал
![]() (3.11)
(3.11)
Тоді можна ввести визначення похідної інтервальної функції:
![]() . (3.12)
. (3.12)
Визначення інтегралу інтервальної функції також має декілька різних формулювань. Але найбільш вірним все ж та легким для сприйняття, це визначення за ідеями Мура.
Припустимо, що f- неперервна функція для якої існує інтервальне розширення F. Припустимо, що функція F є інтервальною функцією, визначеною для Х ![]() А, де А=[а,b], аf (х), при х
А, де А=[а,b], аf (х), при х ![]() А та
f (х)
А та
f (х)![]() F(х) при Х
F(х) при Х![]() А. Функція
А. Функція
g(x) = ![]() ,
,
має неперервну похідну g’(x)=f(x) та згідно теореми про середнє
g(x)=g(a)+f(a+?·(x-a))(x-a),
для деякого ? ![]() [0,1]. Так як g(a)=0, відповідно
[0,1]. Так як g(a)=0, відповідно
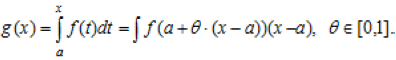
Тоді
![]()
а так як х![]() [a,b] і х
[a,b] і х![]() а, то
а, то
![]()
Звідси для будь-якого Х=![]() , позначивши
, позначивши![]() через
через![]() або
або ![]() маємо
маємо
![]() (3.13)
(3.13)
Використовуючи властивість адитивності інтегралу:
![]() ,
,
отримаємо
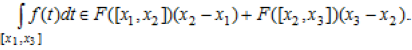 (3.14)
(3.14)
Формула (3.12) дає підстави для введення поняття інтервального інтегралу від інтервальної функції.
Якщо f – неперервна інтервальна функція дійсної змінної, та F-неперервне
інтервальне розширення f, таке що F(х) = f (х), то інтеграл визначається як:
![]() . (3.15)
. (3.15)
Якщо f – неперервна інтервальна функція дійсної змінної ![]() , то існує пара неперервних дійсних функцій f1 і f2 таких, що
, то існує пара неперервних дійсних функцій f1 і f2 таких, що ![]() , і введене визначення інтегралу рівносильне наступному:
, і введене визначення інтегралу рівносильне наступному:
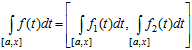 . (3.16)
. (3.16)