7.5.3 Застосування ДПФ

 

Часто ДПФ застосовується для дослідження та аналізу спектра сигналу. При цьому зазвичай найбільш цікавими є лише амплітуди С_к окремих гармонік, а не їх фази. У цьому випадку спектр зазвичай відображається у вигляді графіка залежності амплітуди від частоти. Часто шкала амплітуд градуюється в децибелах. Децибели вимірюють не самі амплітуди, а їх відношення. Наприклад, різниця на 20 дБ означає відмінність амплітуд у 10 разів, різниця на 40 дБ означає відношення амплітуд у 100 разів. Відмінності амплітуд в 2 рази відповідає різниця приблизно в 6 дБ. Шкала частот також часто градуюється в логарифмічному масштабі.

Перед обчисленням спектру сигналу потрібно вибрати відрізок сигналу, на якому буде обчислюватися спектр. Довжина відрізка повинна бути ступенем двійки (для роботи ШПФ), інакше сигнал треба доповнити нулями до потрібної довжини. Після цього до обраної ділянки сигналу застосовують ШПФ.

Коефіцієнти амплітуд розраховують за формулою .

При обчисленні спектру зазначеним методом можливий наступний небажаний ефект. При розкладанні функції в ряд Фур'є вважається, що функція періодична, з періодом, рівним розміру ШПФ. Обчислюється спектр саме такої функції, а не тієї, сегмент якої використовується. При цьому на границях періодів така функція напевно буде мати розриви (адже вихідна функція не була періодичною). А розриви у функції сильно впливають на її спектр, спотворюючи його.

Для усунення цього ефекту застосовуються так звані вагові вікна. Вони плавно зменшують значення функції поблизу країв ділянки, що аналізується. Вагові вікна мають форму, схожу на гауссіан. Обрану для аналізу ділянку сигналу множать на вагове вікно, яке усуває розриви функції при «зацикленні» даної ділянки сигналу. «Зациклення» відбувається при ДПФ, так як алгоритм ДПФ вважає, що функція періодична. Існує безліч вагових вікон, названих на честь їх творців. Всі вони мають схожу форму і в значній мірі усувають розглянуті спотворення спектра. Наведемо формули двох вікон: Хемінга і Блекмена (рис. 1.8):

 

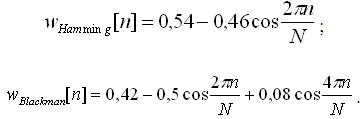
В даному випадку вікно застосовується до сигналу з індексами від 0 до N. Вікно Хеммінга використовується найбільш часто. Вікно Блекмана має більш сильну дію при усуненні розглянутих спотворень, проте має свої недоліки.

Важлива властивість спектрального аналізу полягає в тому, що не існує жодного, єдино правильного спектру будь-якого сигналу. Спектр можна обчислювати із застосуванням різних розмірів ШПФ і різних вагових вікон. Для кожної конкретної задачі необхідно використовувати свої способи.

Ще одна важлива властивість полягає в тому, що при розкладанні в спектр ми знаходимо не ті синусоїдальні складові, з яких складався вихідний сигнал, а лише знаходимо, з якими амплітудами потрібно взяти певні кратні частоти, щоб отримати вихідний сигнал. Проте зазвичай (особливо при використанні вагових вікон) цього майже не помітно за графіком спектру, тобто графік спектру досить адекватно відображає саме частоти вихідного сигналу.

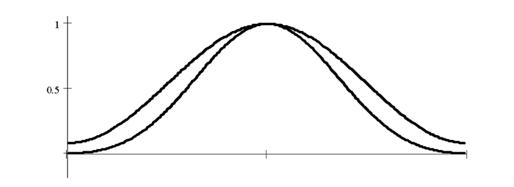
Рисунок 1.7 – Вагові вікна Хемінга (верхнє) і Блекмана (нижнє)

 

7.5.4. Ортогональні перетворення в діадних базисах

 

Ортогональні перетворення (orthogonal transformation) в діадних (або двозначних знакозмінних) базисах визначені для даних, представлених векторами довжиною . До таких перетворень належать перетворення Адамара, Пелі, Уолша, Трахтмана, і ряд інших. Матриця ядра кожного з подібних перетворень містить цілочислові коефіцієнти з множини {-1; +1}. Очевидно, що при виконанні подібних перетворень істотно скорочується обсяг обчислень за рахунок виключення множення в кожній базовій операції.

Матриця ядра перетворення Уолша-Адамара для може бути описана як результат кронекерівського добутку m матриць ДЕФ розміром 2х2:

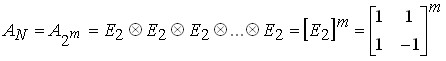
де символ – операція кронекерівського множення векторів, у результаті чого породжується матриця блочної структури. Помітимо, що операція кронекерівського множення двох матриць полягає в одержанні блочної матриці, блоками якої є помножена на відповідний елемент правої матриці ліва матриця, тобто:

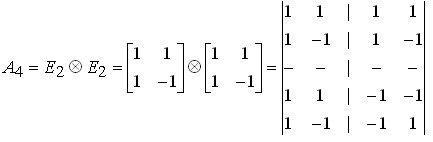
Матриця Адамара для

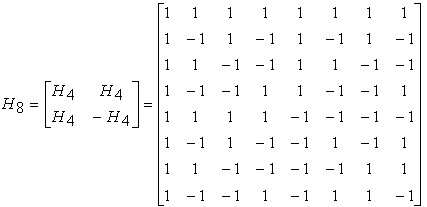
Матриця ядра Адамара має наступні властивості:

1) циклічність ;

2) мультиплікативність;

3) симетричністю .

У завданнях ЦОС використовуються також інші, подібні Адамару, перетворення – Пелі, Уолша, Трахтмана та інших. Ядра (матриці) цих перетворень можуть бути отримані на основі матриці ядра перетворення Адамара при певному перевпорядкуванні рядків.