7.5.2 Дискретне перетворення Фур’є

 

Дискретне перетворення Фур'є (ДПФ) є базовим алгоритмом цифрової обробки сигналів у частотній області. Завдяки наявності ефективних алгоритмів його обчислення – алгоритмів швидкого перетворення Фур'є (ШПФ) – ДПФ широко використовується для цілей цифрової фільтрації та спектрально-кореляційного аналізу сигналів.

Для сигналу, заданого у вигляді дискретної послідовності , пряме й обернене дискретне перетворення Фур'є (ДПФ) має вигляд

;          (1.7)

,           (1.8)

де k – номер гармоніки із частотою , N – обсяг вибірки. , визначений як комплексний спектр сигналу, можна представити

,                     (1.9)

де амплітудно-частотна (АЧХ) і фазо-частотна характеристика (ФЧХ) сигналу відповідно визначаються

;                              (1.10)

.                         (1.11)

Обернене ДПФ можна також виконати за допомогою співвідношення

.           (1.12)

Виходячи з (1.12), оцінку форми сигналу при використанні тільки інформації про його ФЧХ можна зробити:

                    (1.13)

Якість відновлення сигналів можна поліпшити додатково використовуючи в (1.13) різні вагові функції, наприклад, трикутну, експонентну й ін. Тоді вираз (1.13) можна переписати в наступній формі

,               (1.14)

де – прийнята вагова функція.

Похибку, що виникає при відновленні сигналу, можна оцінити за середнім значенням квадрата похибки:

.                        

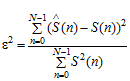Іншою відомою формою запису ДПФ є рівняння:

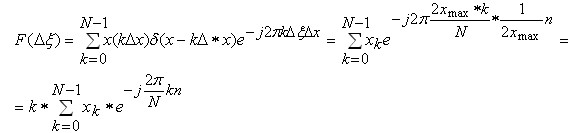
де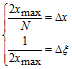

Тоді легко отримати, що

Подібним способом можна отримати і для оберненого перетворення

Таким чином, в матричній формі:

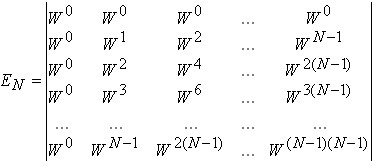
де , а сама матриця ядра ДПФ називається матрицею дискретних експоненціальних функцій (ДЕФ, discrete exponential function). При цьому рядки матриці визначають набір ортогональних функцій або базис розкладання.

При виконанні перетворення Фур'є рядки матриці ядра задають набір ортогональних функцій, по яких виконується розкладання вихідного сигналу. Кожний елемент вектора результату визначає внесок відповідної ортогональної функції у формування вихідного сигналу. Для перетворення Фур'є, як і для будь-якого ортогонального перетворення, визначник матриці ядра перетворення відмінний від "0", що дозволяє виконати як пряме, так і обернене перетворення:

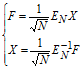
оскільки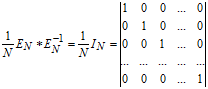

Обчислення перетворень Фур'є вимагає дуже великого числа множень (приблизно N²) і обчислень синусів. Існує спосіб виконати ці перетворення значно швидше: приблизно за операцій множення. Цей спосіб називається швидким перетворенням Фур'є. Алгоритм ШПФ – це спосіб швидкого обчислення ДПФ , що дозволяє усунути притаманну ДПФ надмірність. Вони ґрунтуються на властивостях комплексної експоненти, для зручності позначають (), її симетрії і періодичності з періодом, рівним довжині оброблюваної реалізації сигналу N (числу точок ШПФ). Відповідно до останньої властивості експоненті відповідає період N/p, де p – цілі числа, на які ділиться N. Використання даних властивостей в алгоритмах ШПФ виключає велике число повторюваних при обчисленні ДПФ операцій.

У результаті швидкодія ШПФ може залежно від N в сотні разів перевершувати швидкодію стандартного алгоритму. При цьому слід підкреслити, що алгоритм ШПФ є точним. Він навіть точніше стандартного, тому що скорочуючи число операцій, він призводить до менших помилок округлення.

Однак у більшості алгоритмів ШПФ є особливість: вони здатні працювати лише тоді, коли довжина аналізованого сигналу N є ступенем двійки. Зазвичай це не є великою проблемою, так як аналізований сигнал завжди можна доповнити нулями до необхідного розміру. Число N називається розміром або довжиною ШПФ

У випадку зображень, що представляють собою двовимірний сигнал, спектром є також двовимірний сигнал. Базисні функції перетворення Фур'є мають вигляд добутків

 

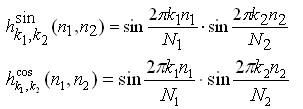
де розмір вихідного сигналу, він же – розмір спектру. – це номера базисних функцій (номера коефіцієнтів двовимірного ДПФ, при яких ці функції знаходяться). Оскільки розмір спектру дорівнює розміру вихідного сигналу,то , – змінні-аргументи базисних функцій. Оскільки область визначення базисних функцій співпадає з областю визначення сигналу, то .

Двовимірне ДПФ визначається наступними формулами ( – вихідний сигнал, а – його спектр:

.

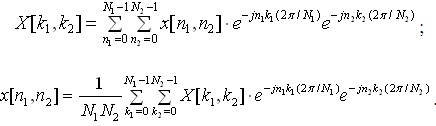
Безпосереднє обчислення двовимірного ДПФ за наведеними формулами вимагає величезних обчислювальних витрат. Однак можна довести, що двовимірне ДПФ має властивість сеперабельності, тобто його можна обчислити окремо по двох вимірах. Для обчислення двовимірного ДПФ достатньо обчислити одновимірні комплексні ДПФ всіх рядків зображення, а потім обчислити в результуючому «зображенні» одномірні комплексні ДПФ всіх стовпців. При цьому результати всіх одновимірних комплексних ДПФ потрібно записувати на місце вихідних даних для цих ДПФ. Наприклад, при обчисленні одновимірного ДПФ першого рядка зображення потрібно результат ДПФ записати в перший рядок цього зображення (він має той же розмір). Для цього потрібно кожний піксель зберігати у вигляді комплексного числа.

Таким чином, ефективний алгоритм обчислення ДПФ зображення полягає в обчисленні одновимірних ШПФ спочатку від всіх рядків, а потім-від всіх стовпців зображення.