8.1.3. Фільтрація зображень
Зазвичай зображення, сформовані різними інформаційними системами, спотворюються дією завад. Це ускладнює як їхній візуальний аналіз, так і автоматичну обробку. При вирішенні деяких завдань обробки зображень у ролі завад можуть виступати ті або інші компоненти самого зображення. Наприклад, при аналізі космічного знімка земної поверхні може стояти завдання визначення границь між її окремими ділянками - лісом і полем, водою й сушею тощо. З погляду цього завдання окремі деталі зображення всередині розділених областей є завадою.
Ослаблення дії завад досягається фільтрацією. При фільтрації яскравість (сигнал) кожної точки вихідного зображення, спотвореного завадою, замінюється деяким іншим значенням яскравості, яке в меншій мірі було спотворене завадою. Фільтрація зображень здійснюється в просторовій і частотній областях. При просторовій фільтрації зображень перетворення виконується безпосередньо над значеннями відліків зображення. Результатом фільтрації є оцінка корисного сигналу зображення. Це досягається завдяки тому, зображення часто являє собою двовимірну функцію просторових координат, що змінюється по цих координатах повільніше, ніж завада, що також є двовимірною функцією. Це дозволяє при оцінці корисного сигналу в кожній точці зображення взяти до уваги сусідні точки, скориставшись певною подібністю сигналу. В інших випадках, навпаки, ознакою корисного сигналу є різкі перепади яскравості. Однак, як правило, частота цих перепадів відносно невелика, так що на значних проміжках сигнал або постійний, або змінюється повільно. І в цьому випадку властивості сигналу проявляються при спостереженні не тільки його окремої точки, але й при аналізі її околиці. Поняття околиці є досить умовним. На рисунку 2.3 представлена ієрархія околиць відліку, позначеного"0".
"1" позначена околиця першого порядку, для якої відстань між елементами дорівнює 1. "2" позначена околиця другого порядку, до якої ставляться діагональні елементи, відстань від яких до центрального відліку "0" дорівнює 
. Околиця третього порядку представлена елементами, що знаходяться від центрального елемента на відстані 2, і так далі.
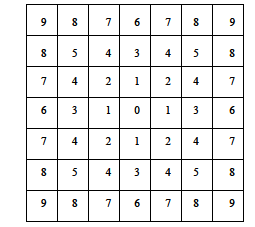
Рисунок 2.3 – Конфігурації околиці елемента "0" у кадрі зображення в ієрархічній послідовності.
Відповідно до рисунка 2.3 формується ієрархія конфігурацій околиці центрального відліку розглянутого фрагмента кадру по зростанню відстаней від нього до відліку околиці. Околиця може бути утворена лише найближчими сусідами, але може містити й досить багато елементів кадру. При розгляді околиці великого розміру, іноді встановлюється різний ступінь впливу далеких і близьких від центра околиці точок на сигнал, формований на виході фільтра в даній точці кадру. Таким чином, ідеологія фільтрації ґрунтується на використанні як даних поточної точки, так і її околиці.
Традиційна фільтрація в частотній області вимагає виконання наступної послідовності перетворень:
Завдання полягає в тому, щоб знайти таку обчислювальну процедуру, що забезпечила б одержання найкращих результатів.
Використання фільтрів для аналізу текстурованих зображень аналогічно спектральному аналізу але має ряд переваг в тих випадках, коли характерні ознаки спектру зображення відомі. Фільтрація дозволяє більш точно розділити сигнал на складові, що відповідають різним частотним смугам.
8.1.3.1. Оптимальна лінійна фільтрація.
Нехай 
– значення яскравості зображення – корисного сигналу на перетині 
-го рядка та 
-го стовпця, а зображення , що знаходиться на вході фільтра описується моделлю:
(2.12)
де 
– значення завади в точці з координатами 
, 
– функція, що описує взаємодію сигналу і завади, а I та J – відповідно число рядків і стовпців у кадрі.
Надалі будемо дотримуватися прийнятої при цифровій обробці зображень декартової системи координат з початком у лівому верхньому куті кадру та з позитивними напрямками із цієї точки вниз та вправо.
При лінійній фільтрації вихідний ефект визначається лінійною комбінацією вхідних даних:
(2.13)
В цьому рівнянні 
– результат фільтрації корисного сигналу в точці кадру з координатами
; S – множина координат точок, що утворюють околицю; 
- вагові коефіцієнти, сукупність яких являє собою двовимірну імпульсну характеристику (ІХ). Якщо область кінцева, то імпульсна характеристика має кінцеву довжину й фільтр називається КІХ- фільтром. В іншому випадку імпульсна характеристика має безкінечну довжину, а фільтр назву БІХ- фільтра. У виразі (2.13) прийнято, що ІХ не залежить від координат точки, у якій визначається вихідний ефект. Процедури обробки зображень, що володіють властивістю незалежності від координат, називаються однорідними.
Найбільш поширеним критерієм оптимальності який використовується для оцінки якості обробки зображень є критерій мінімуму середньоквадратичної похибки. Для фільтрації запишемо його вираз наступним чином:
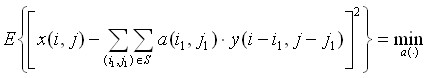(2.14)
де 
– символ математичного очікування. Згідно (2.14) пошук оптимального фільтра заклечається в визначенні його ІХ таким чином, щоб середній квадрат похибки 
, який виражає різницю між сигналом 
і його оцінкою 
, яка формується фільтром, був мінімальний. Математичне сподівання обчислюється по всім випадковим величинам, які є в (2.14), що свідчить про орієнтацію критерія на врахування середніх похибок.
Розглянемо реалізацію лінійної фільтрації в середовищі Matlab.
Синтаксис:
D=filter2(h,S)
D=filter2(h,S, shape)
Вбудована функція D=filter2(h,S) виконує фільтрацію даних, заданих в двомірному масиві S, двовимірним КІХ фільтром, коефіцієнти якого зведені в матрицю h, яку також називають маскою фільтра. Як правило, D і S є на півтоновими зображеннями. Результат фільтрації, що повертається в матриці D, обчислюється як двовимірна згортка, яка виконується за допомогою функції conv2.
Результат роботи функції D=filter2(h,S, shape) залежить від значення параметра shape. Якщо параметру присвоєно значення ‘same’, то в D повертається центральна частина згортки, розмір якої дорівнює розміру вихідних даних – S. Цей параметр використовується по замовчуванні. Якщо параметру присвоєно значення ‘full’ то повертається весь результат згортки. При цьому size(D)>size(S). Якщо параметру присвоєно значення valid, повертається лише та частина згортки, при обчисленні якої не використовувались краєві частини вихідних даних, доповнені нулями. Прицьому size(D) В залежності від складності зображення використовують два або більше двохвимірних фільтрів з коротко-імпульсною характеристикою (КІХ) або банки вузько смугових фільтрів виду де Для фільтрації зображень на основі їх спектральних ознак використовують фільтри Габора. Імпульсна характеристика фільтра має вигляд Вона поєднує гаусову функцію та гармоніку, що характеризує частотну характеристику зображення. За допомогою параметрів дисперсії Алгоритм класифікації та розпізнавання зображень включає наступні етапи: 1) фільтрація зображення за допомогою набору фільтрів; 2) обчислення потужності на виході кожного з фільтрів; 3) згладжування значень потужності; 4) нормалізація значень потужності; 5) класифікація (розпізнавання) за допомогою шаблонів або співвідношень значень потужності. Недоліком даного методу є те, що він потребує значного об’єму обчислень в тому разі, коли розмір фільтра У практиці цифрової обробки зображень широко використовується маскова фільтрація. Її лінійний різновид є одним з варіантів двовимірної фільтрації з кінцевою імпульсною характеристикою (КІХ) фільтра. Як маска використовується безліч вагових коефіцієнтів, заданих у всіх точках околиці S , що зазвичай симетрично оточують поточну точку кадру. 
, (2.15)
та 
відповідно фільтрований сигнал та сигнал зображення, 
– імпульсна характеристика розміром 
. В якості критерію оптимальності використовують співвідношення середніх значень сигналів на виході фільтра, що отримані для текстури, що відповідає характеристиці фільтра, та для текстур, що не відповідають характеристиці фільтра. 
(2.16)
в (2.16) регулюють смугу частотного фільтра з парою центральних частот 
по двом просторовим координатам. Як правило, для характеристики текстурованого зображення використовують набір фільтрів з фіксованими або визначеними для кожної текстури парами частот.
значний і число фільтрів велике. 
