8.1.3.2 Нелінійна фільтрація

У результаті застосування лінійних фільтрів, що згладжують, відбувається придушення шумів, але одночасно розмиваються границі між областями з різною амплітудою сигналу. Для зменшення кількості розмитих границь розроблені різні нелінійні фільтри. Як і лінійні КІХ фільтри, нелінійні фільтри працюють у ковзному вікні. Різниця між лінійною та нелінійною фільтрацією полягає в тому, що при лінійній фільтрації обчислюється лінійна комбінація відліків сигналу, а при нелінійній фільтрації виконуються нелінійні перетворення відліків сигналу в околиці елементів, які обумовлюються маскою фільтра.

Сігма-фільтр

Сігма-фільтр призначений для придушення шумів у зображенні зі збереженням контурів (різких границь областей). Центральний елемент маски заміщується зваженим середнім значенням, обчисленим лише по тим амплітудам відліків, значення яких попадають в – область вибрана згідно яскравості центрального елемента. вибирається або як середньоквадратичне відхилення (СКВ) шуму, що придушується, або як СКВ в масці, або встановлюється рівною СКВ, отриманому по всьому зображенню:

(2.16)

де – околицю становлять ті значення координат маски, у яких виконується накладена умова:

(2.17)

– КІХ лінійного згладжуючого фільтра.

При k = 2 діапазон значень, які замінюються становить , у випадку нормального розподілу шуму ймовірність попадання амплітуди за межі діапазону дорівнює 4,55%.

Медіанний фільтр

Медіанний фільтр (МФ) замінює центральний елемент маски медіаною впорядкованої вибірки, сформованої зі всіх амплітуд відліків, що покриваються маскою фільтра. При застосуванні МФ відбувається послідовна обробка кожної точки кадру, у результаті чого утворюється послідовність оцінок. При медіанній фільтрації використовується ковзне двовимірне вікно. У принципі, для кожного відліку виконується незалежна оцінка медіани у вікні. З метою прискорення оцінки доцільно алгоритмічно на кожному кроці використовувати раніше виконані обчислення. Розмір вікна встановлюється непарним і рівним . Відліки зображення, що знаходяться в межах вікна, утворюють робочу вибірку поточного відліку. Якщо впорядкувати послідовність по зростанню, то її медіаною буде той елемент вибірки, що займає центральне положення в цій упорядкованій послідовності. Цей елемент є найбільшим і найменшим значенням у вибірці й визначає результат медіанної фільтрації для поточної точки кадру. Введемо позначення описаної процедури у вигляді:

(2.18)

Розглянемо приклад. Припустимо, що впорядкована послідовність Y у вікні розміром 3x3 має вигляд: Y={76,100,69,120,210,143,87,130,155} де елемент 210 відповідає центру вікна (x, y). Велике значення яскравості в цій точці кадру є результатом впливу імпульсної перешкоди. Упорядкована по зростанню вибірка має вигляд: {69,76,87,100,120,130,143,155,210}, отже, відповідно до розглянутої вище процедури (2.18), на виході медіанного фільтра одержуємо . Бачимо, що врахування яскравостей елементів околиці при фільтрації в поточній точці призвів до придушення імпульсної завади. Якщо імпульсна завада не є точковою, а займає деяку область, то вона також може бути подавлена, якщо розмір цієї локальної області буде менше, ніж половина розміру апертури МФ. Тому для придушення імпульсних завад, що вражають локальні ділянки зображення, варто збільшувати розміри апертури МФ.

З (2.8) слідує, що дія МФ полягає в "ігноруванні" як позитивних, так і негативних викидів значень вхідної вибірки. Такий принцип придушення завад може бути застосований і для ослаблення шуму на зображенні. Однак дослідження придушення шуму за допомогою медіанної фільтрації показує, що її ефективність при рішенні цього завдання нижче, ніж у лінійної фільтрації. Медіанна фільтрація краще зберігає границі зображення, ніж будь-яка лінійна фільтрація.

Медіанні фільтри придушують імпульсні шуми. До таких шумів відноситься шум типу "сіль і перець", відліки якого мають значення, що відповідають максимальному ("сіль") і мінімальному ("перець") рівням квантування в сигналі зображення. Різкі зміни амплітуди зберігаються медіанним фільтром, а імпульсна завада, розмір якої таким фільтром придушується. Однак при збільшенні маски фільтра можна втратити інформацію про малорозмірні області зображення та призвести до спотворення границь областей, особливо в кутових положеннях.

Оскільки застосування МФ призводить до придушення високих частот зображення, викликаючи розмивання країв і текстур, все більший розвиток отримують схеми адаптивної фільтрації, які дозволяють змінити імпульсну характеристику фільтра залежно від локального значення сигналу зображення.

Один з алгоритмів адаптивної медіанної фільтрації (АМФ) виконується таким способом. У вікні фільтрації оцінюються мінімальне значення сигналу , максимальне значенняі медіана . Фільтрації піддається тільки той центральний елемент вікна f (x, y), для якого виконується умова 2.19 а): значення медіани більше мінімального й менше максимального значень у вікні й не виконується умова 2.19 б): значення сигналу в центрі вікна більше мінімального й менше максимального значень у вікні.

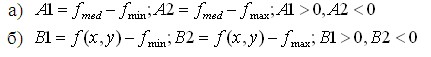         (2.19)

Застосування такого фільтра дозволяє видалити біполярну імпульсну заваду, забезпечити згладжування шумів і зменшити придушення високих частот у зображенні.

На рисунку 2.4 наведено приклад усунення шуму за допомогою медіанного фільтра.

У системі Matlab (Іmage Processіng Toolbox) існує можливість формування й накладення на зображення трьох типів шумів. Для цього використовується вбудована функція іmnoіse, що призначена, в основному, для створення тестових зображень, що використовуються при виборі й дослідженні методів фільтрації шуму. В даному випадку, на зображення був накладений імпульсний шум за допомогою команди

J = imnoise(I,'salt & pepper',0.02);

Для наочного порівняння приведемо три зображення разом: вихідне, зашумлене та відновлене. Як видно з рисунку 2.4 вихідне та відновлене зображення майже не відрізняються один від одного.

Рисунок 2.4 – Приклад застосування медіанної фільтрації

8.1.3.3. Інверсні фільтри в задачах обробки зображень

Інверсна фільтрація (inverse filtering) широко застосовується в обробці зображень для розв’язання таких задач як відновлення зображень, що вражені шумом, усунення розмиття, покращення контрастності. В задачах розпізнавання об’єктів та образів інверсні фільтри використовують як допоміжні засоби для покращення зображення в цілому перед операцією розпізнавання. Задача лінійної інверсної фільтрації полягає в тому, щоб за допомогою даних вимірювань у вигляді матриці елементів зображення відновити оригінальну матрицю зображення за умови, що матриці зв’язані деяким оператором з імпульсною характеристикою розміром і присутній адитивний шум з відомою кореляційною характеристикою. Формально задачу можна записати у вигляді рівняння

                         (2.20)

Метод розв’язку рівняння (2.20), що став класичним, дав Н. Вінер , його представлено функцією Matlab wiener2. Метод оснований на перетворенні Фур’є. Однак, застосування методу має ряд перешкод:

 для розв’язання рівняння (2.20) потрібно знайти оцінку імпульсної характеристики, що є самостійною непростою задачею.

У зв’язку з означеними проблемами часто використовують більш простий підхід до розв’язання рівняння (2.20), що нехтує складовою шуму. Для знаходження матриці оригінального зображення використовують метод дискретного перетворення Фур’є (ДПФ). Позначимо оператор ДПФ як , обернений йому як , матрицю даних зображення як . Тоді

де – функція спектрального вікна, – функція регуляризації.

Слід відзначити, що розмір імпульсної характеристики, як правило, рівний розміру зображень, тому перетворення ДПФ виконують з використанням всієї множини елементів матриць зображень. Це є причиною того, що метод інверсної фільтрації не застосовують до розв’язання задач розпізнавання об’єктів та аналізу динамічних текстур як основний засіб фільтрації ознак.

Розглянемо задачу інверсної фільтрації з точки зору ідентифікації динамічних систем і сформулюємо її у формі, що дозволить виконувати фільтрацію ознак динамічних текстур.

Нехай задана двохвимірна функція Хевісайда

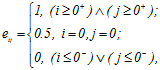                         (2.21)

зображення текстурованого фону задано в області і є відкликом лінійної динамічної систему на збудження виду (2.21), його можна представити як

                              (2.22)

де – перехідна характеристики системи розміром , що значно менший розміру зображення. Поставимо задачу відтворення за допомогою інверсного фільтра з перехідною характеристикою сигналу збудження в (2.22), що є постійною величиною в межах зображення. Тоді

                         (2.23)

де – константа, – відліки шуму, що зв’язані з наближеним характером інверсного фільтра по відношенню до сигналу фону.

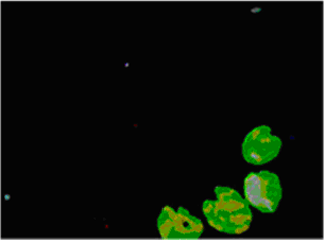
Рисунок 2.5 – Розпізнавання об’єктів за методом інверсної фільтрації

 

Розглянемо даний метод на прикладі, в якості тестового зображення використаємо рис.2.2. Як видно з рисунка 2.5, зображення практично вільне від зайвих елементів, великі об’єкти не спотворені. В результаті фільтрації втрачено найменший світлий елемент, але виділено темний елемент біля верхньої границі зображення.