
9.4. Інтервальні методи розв’язання диференційних рівнянь
Цікавість до використання інтервальних методів при вирішенні диференційних рівнянь пояснюється тим, що в рамках інтервального аналізу вхідні дані диференційного рівняння можуть бути задані у вигляді інтервалів, і отримані рішення враховують не лише помилки у вхідних даних, але й помилки апроксимації і округлення.
При інтервальному моделюванні ІВС, однією з задач є розв’язання диференційних рівнянь з інтервальними даними. На сьогодняшній день розроблено багато інтервальних методів розв’язку диференційних рівнянь. Розглянемо детально найвідоміші методи.
9.4.1. Інтервальний метод другого порядку для розв’язку звичайних диференційних рівнянь
Розглянемо задачу Коші
![]() , (3.17)
, (3.17)
![]() . (3.18)
. (3.18)
Припустимо, що функція f(y) визначена і має дві перші обмежені похідні на інтервалі A=[a,b].
Розглядаємий нижче метод розв’язку задачі (3.17), (3.18) припускає неточно задані початкові дані, а саме припустимо, що існує інтервал Y0 такий, що він лежить строго в А і y0ÎY0. Окрім того припустимо, що функція f(y) має інтервальне розширення F(Y), що володіє наступними властивостями:
1) Функція F(Y) визначена і неперервна при всіх YÌA;
2) функція F(Y) монотонна по включенню, тобто з того, що Y1ÌY2, слідує F(Y1)ÌF(Y2);
3) існує число l>0 таке, що ![]() для всіх Y?A, а також існує
для всіх Y?A, а також існує ![]() - інтервальне розширення функції
- інтервальне розширення функції ![]() , що визначене при YÌA і монотонне по включенню.
, що визначене при YÌA і монотонне по включенню.
Оскільки Y0 лежить в А, для деякого скінченного h0>0, знайдеться таке число ξ>0, що
![]() .
.
Інтервальний розв’язок побудуємо на відрізку [0, ?], для цього розіб’ємо його на m частин точками ![]() (i=0,1,…,m), h= ?/m
(i=0,1,…,m), h= ?/m
Теорема 3.2 Якщо інтервали Y(xi)=Yi (i=0,1,…,m) визначаються формулами
Y0=Y(x0)=Y(0), (3.19)
Yi+1=Yi+(h/2){F(Yi)+F(Yi+hF(Yi+[0,h]?F(A)))-(h3/12)?(Yi+[0,h]·F(A))}, (3.20)
(i=0,1,…,m),
то для будь-якого розв’язку y(x) рівняння (3.17), такого, що y(0)ÎY0, справедливі включення y(хi)ÎYi(i=1,…,m) і має місце наступна оцінка для ширини інтервалівYi:
![]() , (3.21)
, (3.21)
де N і М – дійсні константи, що не залежать від i i h.
9.4.2. Інтервальні методи типу Рунге-Кутта
Розглянемо задачу Коши:
![]() , (3.22)
, (3.22)
![]() . (3.23)
. (3.23)
Припустимо, що функція f(x,y) визначена для всіх ![]() , де
, де ![]() .
.
Так як ряд параметрів, що визначаються формулами метода Рунге-Кута, використовуються при побудові відповідних інтервальних формул, розглянемо спосіб отримання розв’язку цим методом в класичній математиці.
Для знаходження y(x+h), якщо відомо y(x) використовується наступна формула:
![]() , (3.24)
, (3.24)
де ![]()
![]()
а величини a2, …, aq, p1, …, pq,
bij (0
Нехай функція f(x,y) має інтервальне розширення F(X,Y), що має наступні властивості:
1. F(X,Y) визначене і неперервне для всіх ХÌDх, YÌDy;
2. F(X,Y)монотонне по включенню, тобто з Х1ÌХ, Y1ÌYслідує, що F(X1,Y1)ÌF(X,Y);
3. Існує константа L>0, така, що ![]() для всіх
ХÌDх, YÌDy, де
для всіх
ХÌDх, YÌDy, де ![]() . Нехай, окрім цього, y(x,y) має інтервальне розширення Y(X,Y), визначене для всіх
ХÌDх, YÌDy і монотонне по включенню.
. Нехай, окрім цього, y(x,y) має інтервальне розширення Y(X,Y), визначене для всіх
ХÌDх, YÌDy і монотонне по включенню.
Тоді розв’язок інтервального диференційного рівняння буде наступним:
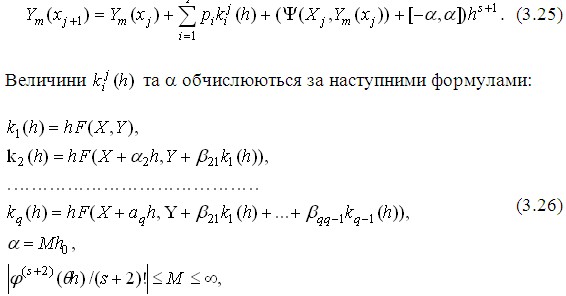
де s – порядок рівняння.
Цей метод справедливий і для розв’язку рівнянь зі змінним кроком, а також для систем рівнянь вигляду (3.22) з відповідними початковими умовами.
9.4.3 Метод Крукеберга
Трьохкроковий метод Крукеберга чисельного розв’язання задачі Коши для звичайних диференційних рівнянь дозволяє отримати інтервали, що містять розв’язок задачі. В ньому попередньо будується інтервальний розв’язок для фіксованої дійсної задачі з певнимим початковими значеннями з заданої множини (інтервалу), а потім методом збурень знаходяться інтервальні включення для всіх можливих рішень.
Нехай рівняння першого порядку ![]() з початковими умовами y(x0)=y0 має єдиний розв’язок
з початковими умовами y(x0)=y0 має єдиний розв’язок ![]() на [x0,x1]. Якщо початкові дані задані неточно, тобто
на [x0,x1]. Якщо початкові дані задані неточно, тобто ![]() , де Y0 - певний інтервал в R, то розв’язки задачі в такій постановці утворюють множину
, де Y0 - певний інтервал в R, то розв’язки задачі в такій постановці утворюють множину ![]() . Необхідно знайти інтервал
. Необхідно знайти інтервал ![]() , де
, де ![]() , x1=x0+h, величина кроку h визначається в процесі розв’язку.
, x1=x0+h, величина кроку h визначається в процесі розв’язку.
На першому кроці знаходимо крок h і інтервальний поліном k-го ступеню Pk(x-x0) такий, що при x1=x0+h, ![]() . Такі поліноми можуть бути отримані за ітераційним алгоритмом Пікара:
. Такі поліноми можуть бути отримані за ітераційним алгоритмом Пікара:
![]() (3.27)
(3.27)
де F – інтервальне розширення функції f. На практиці обмежуються поліномами нульового ступеню p0.
На другому етапі знаходиться інтервальний розв’язок початкового рівняння з дійсними початковими даними y(x0)=d0?Y0. Використовуючи формулу Тейлора, в якій дійсні аргументи замінені інтервальнимим, маємо інтервал
![]()
Зрозуміло, що ![]()
U0=Y0-d0 – всіх можливих збурень початкового значення d0.Перепишемо початкову задачу у вигляді
![]() (3.28)
(3.28)
Нам відомо, що ![]() , необхідно визначити
, необхідно визначити ![]() . Шляхом розкладу правої частини за формулою Тейлора в околі розв’язку
. Шляхом розкладу правої частини за формулою Тейлора в околі розв’язку ![]() і утримуючи члени першогопорядку відносно h, маємо рівняння
і утримуючи члени першогопорядку відносно h, маємо рівняння
![]() , (3.29)
, (3.29)
з початковими умовами (3.28). Тоді інтервал U1=QU0, де ![]() , F – інтервальне розширення функції
, F – інтервальне розширення функції ![]() , і є шуканим розв’язком задачі (3.29), (3.28).
, і є шуканим розв’язком задачі (3.29), (3.28).
Метод Крукеберга природнім чином узагальнюється на випадок системи рівнянь. При цьому ![]() буде матрицею, елементи якої є інтервальними розширеннями функцій.
буде матрицею, елементи якої є інтервальними розширеннями функцій.![]()