9.5. Представлення інтервальної функції через граничні дійсні функції
Представлення інтервальної функції через дві граничні дійсні функції є одним з важливих підрозділів інтервального аналізу. Подібне представлення дозволяє замість вивчення інтервальної функції зосередити увагу на двох дійсних функціях. Це не тільки в певних випадках спрощує розрахунки, але і дає змогу уявити як веде себе інтервальна функція в тих або інших випадках, отримати більш точніші результати розрахунків.
Проблема представлення інтервальної функції двома граничними дійсними складається в знаходженні представлення
, (3.30)
де 
- певні дійсні функції, які відповідають визначенню.
Наприклад, якщо на відрізку 0£х£3 розглянемо функцію
F(x)=x2-[2,4]×x+[3,5], (3.31)
тоді f1(t)=x2-4×x+3, f2(t)=x2-2×x+5.
Дійсно, для кожного значення аргументу на протязі інтервалу х Î [0,3] функція (3.31) ставить в відповідності певний інтервал [a,b]. Отже множина значень функції на площині (x,y) являє собою область, обмежену кривими y=x2-4×x+3, y=x2-2×x+5 та відрізками прямих х=0 та х=3.
Процес визначення функцій f1та f2 залежить від того, з яких причин функція F має за своє значення інтервали, тобто чому результат є інтервальним числом. Таких причин можна виділити декілька:
1) функція F є функцією дійсного аргументу х, але константи, що
входять до F, це інтервали;
2) функція F є функцією інтервального аргументу X, але константи,
що входять до F, дійсні числа;
3) аргумент функції F та константи, що входять до її складу, є
інтервали.
Якщо функція F є поліномом виду 
, то граничні функції виражаються як:
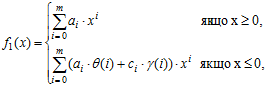(3.32)
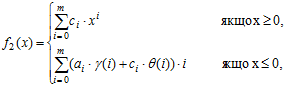(3.33)
де
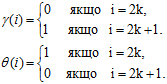
Якщо повернутися до вище наведеного прикладу, то отримаємо:
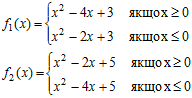
Їх застосуванням визначення граничних функцій дещо змінюється означення диференціалу та інтегралу інтервальної функції.
Так, якщо f - неперервна інтервальна функція дійсного аргументу х?[а,b], то існує пара неперервних дійсних функцій f1 та f2, інтеграл функції можна визначити, як
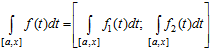. (3.34)
Також можна змінити визначення границі інтервальної функції. Припустимо, що інтервальна функція G задана через дійсні граничні функції: G(х) = [
(х); 
(х)]. Похідна для інтервальноїфункції G(х), що визначена в околиці точки 
, може визначатись за формулою:
. (3.35)
Визначення інтервальної функції через її граничні широко використовується на практиці. Це насамперед пов'язано з тим, що апарат обчислень з дійсними функціями добре розроблений. Припустимо, що ми маємо інтервальний алгоритм, який необхідно реалізувати. Отже,очікувані результати — інтервали. Але з причин округлень, неможливостіотримання "дійсної" області значень інтервальної функції та інше,можливе отримання інтервалів, які значно ширші ніж насправді.
Тому дуже часто ідуть іншим шляхом. Інтервальний алгоритм поділяють на два дійсних. Тоді кожний з дійсних реалізують в рамках інтервальної арифметики. Це не тільки зменшує складність розрахунків для людини, що не досить знайома з інтервальним аналізом, але в певних випадках дозволяє отримати більш точні результати. Але це можливо тільки в випадках, коли представлення інтервальної функції через її граничні можливе і не дуже складне, не займає зайвої кількості часу.
9.6 Розширення інтервальної арифметики
Класична інтервальна арифметика ІR є "неповною" за своїм математичним змістом. Говорячи з математичної точки зору, вона є лише комутативною напівгрупою по додаванню та множенню, а відносно порядку включення вона не є "решіткою". Ця неповнота алгебраїчної та порядкової структури ІR природно стимулює намагання створити на її основі "більш досконалу" інтервальну арифметику. І таке доповнення було зроблено в працях Каухера, а потім вдосконалено в працях Гарденеса та Трепата. Арифметика, що створена в цих наукових працях отримала назву "розширеної інтервальної арифметики" чи "інтервальної арифметики Каухера".
Елементами інтервальної арифметики Каухера, також як і в класичній інтервальній арифметиці, є дійсні пари 
, але вони не обов'язково зв'язані співвідношенням 
. Таким чином, множини інтервалів ІR отримується шляхом приєднання невласних інтервалів , 
, до множини 
власних інтервалів та дійсних чисел. Власні та невласні інтервали, дві половинки ІR, можливо змінювати при відображенні дуалізації:
, (3.36)
такого, що 
.
Додавання та множення на дійсні константи визначається варифметиці Каухера наступним чином:
, (3.37)
(3.38)
Таким чином, кожен елемент х з ІR має один протилежний елемент, що часто визначається як "орр х", і
. (3.39)
Часто в наукових працях можливо зустріти спеціальне позначення для операції, що є зворотною до додавання - алгебраїчної різниці, через ?:
x? y = x + opp y.
Віднімання та ділення в арифметиці Каухера визначаються як:
х-у = х + (-1)-у,
при умові, що 0?y
Крім того в інтервальній арифметиці Каухера зберігається монотонність інтервальних операцій по включенню:
(3.40)
де * Î {+,-, ×,/},х, х', у, у' є ІR.
Дії над векторами та матрицями в розширеній інтервальній арифметиці Каухера визначають подібно тому, як це робиться в класичній арифметиці. Сума (різність) двох інтервальних матриць однакового розміру є інтервальна матриця того ж самого розміру, яка утворюється з по-елементних сум (різностей) операндів. Якщо A=(aij) Î IRm´1, A=(bij) Î IR1´n то результатом їх множення є матриця С=(cij) Î IRm´n така, що
.
Багато визначень та понять класичної інтервальної арифметики без змін переносяться на арифметики Каухера. Тому фактично Каухер не змінив основ, а тільки вніс певні вдосконалення. Деякі з них суттєво спростили застосування інтервального обчислення на практиці.
Контрольні завдання та запитання
1. Навести практичні приклади використання методів інтервального аналізу.
2. Сформулювати основні правила операцій над інтервалами.
3. Скласти алгоритми та програми реалізації найпростіших математичних операцій над інтервалами.
4. Представити у інтервальному вигляді наступні функції: sin, cos, tan, ctg, exp, ln
5. Скласти алгоритми та програми інтервальної реалізації математичних функцій наведених у п.4
6. Сформулюйте задачу Коші для інтервальних чисел. В чому відмінність інтервальних методів розв’язання диференційних рівнянь від класичних?
7. Чим відрізняється класична інтервальна арифметика від інтервальної арифметики Каухера?
8. Побудувати інтервальне розширення для наступних функцій:
;
.
9. Чи буде наступна функція інтервальним розширенням деякої функції 
? Якщо так, то якої?
а)
;
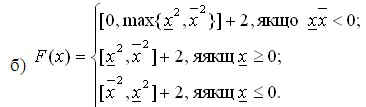
10. Знайдіть інтервальний інтеграл на [a,b] для функції
.
11. Використовуючи формулу Тейлора знайдіть інтервальну оцінку інтеграла
.
12. Побудуйте інтервальний кубічний сплайн на відрізку [0,1] якщо 
, 
, 
, 
.
13. Знайти множину розв’язків системи лінійних алгебраїчних рівнянь
,
де 
; 
13. Розв’яжіть систему рівнянь методом Гаусса
,
де 
; 
