Системи нелінійних рівнянь:

 

function [P,iter] = seidel(G,P,delta,max1)

% Розв'язання систем нелінійних рівнянь ітерацією Зейделя

% Введення - G - нелійна система, записана в формі М-файла G.m

%                - P - початкове наближення до розв'язку

%                - delta - можлива похибка

%                - max1 - число ітерацій

% Вихід      - P - наближення Зейделя до розв'язку

%                - iter - число виконаних ітерацій

N=length(P);

for k=1:max1

X=P;

for j=1:N

A=feval('G',X);

X(j)=A(j);

end

err=abs(norm(X-P));

relerr=err/(norm(X)+eps);

P=X;

iter=k;

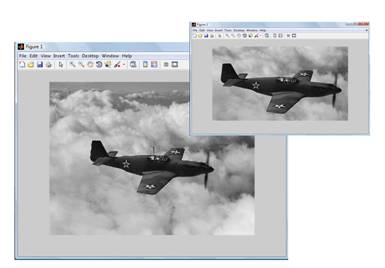
if(err

break

end

end

Функції, що використовувались для запуску даних програм:

function y=f(x)

y=x.^2-1;

function y=df(x)

y=2*x;

function y=fe(x,z)

y=x.^2+1;

function y=g(x)

y=x.^2-2;

function Z=Fz(X)

x=X(1);

y=X(2);

Z=zeros(1,2);

Z(1)=x.^4;

Z(2)=y.^2;

Можливості цифрової обробки зображень в Matlab

На сьогоднішній день система Matlab, зокрема пакет прикладних програм Іmage Processіng Toolbox, є найбільш потужним інструментом для моделювання й дослідження методів обробки зображень. Він включає велику кількість вбудованих функцій, що реалізують найпоширеніші методи обробки зображень. Розглянемо основні можливості пакета Іmage Processіng Toolbox.

Пакет Іmage Processіng надає широкий спектр засобів для цифрової обробки та аналізу зображень. Будучи тісно зв'язаним із середовищем розробки додатків MATLAB, пакет Іmage Processіng Toolbox звільняє користувача від виконання тривалих операцій кодування та налагодження алгоритмів, дозволяючи зосередити зусилля на рішенні основного наукового або практичного завдання.

Основні властивості пакета:

  •  відновлення й виділення деталей зображень;
  •  робота з виділеною ділянкою зображення;
  •  аналіз зображення;
  •  лінійна фільтрація;
  •  перетворення зображень;
  •  геометричні перетворення;
  •  збільшення контрастності важливих деталей;
  •  бінарні перетворення;
  •  обробка зображень і статистика;
  •  колірні перетворення;
  •  зміна палітри;
  •  перетворення типів зображень.

    Пакет Іmage Processіng дає широкі можливості для створення й аналізу графічних зображень у середовищі MATLAB. Цей пакет забезпечує надзвичайно гнучкий інтерфейс, що дозволяє маніпулювати зображеннями, інтерактивно розробляти графічні картини, візуалізувати набори даних і анотувати результати для технічних описів, доповідей і публікацій.

    Пакет Іmage Processіng інтенсивно використовується в більш ніж 4000 компаніях і університетах по усьому світі. При цьому є дуже широке коло завдань, які користувачі вирішують за допомогою даного пакета, наприклад космічні дослідження, військові розробки, астрономія, медицина, біологія, робототехніка, матеріалознавство, генетика й т.д. Він включає велику кількість вбудованих функцій, що реалізують найпоширеніші методи обробки зображень. Розглянемо основні можливості пакета Іmage Processіng Toolbox.

    Геометричні перетворення зображень

    До найпоширеніших функцій геометричних перетворень відносяться кадрування зображень (іmcrop), зміна розмірів (іmresіze) і поворот зображення (іmrotate).

    Суть кадрування полягає в тому, що функція іmcrop дозволяє за допомогою миші в інтерактивному режимі вирізати частину зображення та помістити його в новому вікні перегляду.

         L=imread('airplane.tif');

         imshow(L);

         imcrop;

    Застосування функцій imshow та imcrop

    У пакеті Іmage Processіng Toolbox існує функція іmrotate, що здійснює поворот зображення на заданий кут.

         L1=imrotate(L,35,'bicubic');

         figure,imshow(L1)

    Застосування функціі imrotate

         Таким чином, наведені вище функції дозволяють повертати, вирізати частини, масштабувати, тобто працювати із цілим масивом зображення    

         Аналіз зображень

         Для роботи з окремими елементами зображень використовуються такі функції як іmhіst, іmpіxel, mean2, corr2 та інші.

         Однією з найбільш важливих характеристик зображення є гістограма розподілу значень інтенсивностей пікселів зображення, яку можна побудувати за допомогою функції іmhіst.

         L=imread('cameraman.tif');

         figure, imshow(L);

         figure, imhist(L);

    Застосування функціі imhist

    Досить часто при проведенні аналізу зображень виникає необхідність визначити значення інтенсивностей деяких пікселів. Для цього в інтерактивному режимі можна використовувати функцію іmpіxel.

    L=imread('Air015.jpg');

    c = [12 146 410];

    r = [104 156 129];

    pixels=impixel(L,c,r)

    pixels =

    190 190 190

    187 187 187

    202 202 202

    Ще одною поширеною функцією є функція mean2 – вона обчислює середнє значення елементів матриці.

    B=mean2(L)

    B =

              156.6090

    Функція corr2 обчислює коефіцієнт кореляції між двома матрицями. Інакше кажучи, за допомогою функції corr2 можна сказати наскільки дві матриці зображення схожі між собою. Ця функція широко застосовується при вирішенні завдань розпізнавання.

    Усунення розмитості зображення за допомогою фільтра Віннера

    Віннерівська деконволюція може бути ефективно використана, якщо частота зображення та адитивний шум відомі. В якості приклада використаємо рисунок 5.4 а).

    A=imread('C:\\OLYA\NEW_book\Hibiscus2.jpg');

    imshow(A)

         Зімітуємо розмиття зображення, яке може виникнути під час руху камери. Створимо функцію розсіювання точки (point-spread function - PSF), яка відповідає лінійному зсуву вздовж 31 пікселя (LEN=31), при куті нахилу в 11 градусів (THETA=11). Розмите зображення представлено на рисунку 5.4 б)

         LEN = 31;

         THETA = 11;

         PSF = fspecial('motion',LEN,THETA);

         blurred = imfilter(I,PSF,'circular','conv');

         figure, imshow(blurred);

        

         Для того, щоб підтвердити важливість визначення вірного значення PSF, виконаємо три етапи відновлення. Для першого відновлення wnr1 використаємо PSF, створену на попередньому кроці – рисунок 5.4 в)

         wnr1 = deconvwnr(blurred,PSF);

         figure, imshow(wnr1);

        

         Для кращої наочності добавимо адитивний шум – рисунок 5.4 г)

         noise = 0.1*randn(size(I));

         blurredNoisy = imadd(blurred,im2uint8(noise));

         figure, imshow(blurredNoisy);

    Відновимо розмите та зашумлене зображення використавши інверсну фільтрацію та порівняємо з рисунком 5.4 в). Але врахуємо, що в цьому випадку зображення було не лише розмите, але й зашумлене – рисунок 5.4 д)

         wnr4 = deconvwnr(blurredNoisy,PSF);

         figure, imshow(wnr4);

    Для контролю посилення шуму передбачимо значення відношення шум - сигнал (noise-to-signal power ratio – NSR) – рисунок 5.4 е)

         NSR = sum(noise(:).^2)/sum(im2double(I(:)).^2);

         wnr5 = deconvwnr(blurredNoisy,PSF,NSR);

         figure, imshow(wnr5);

    Змінимо значення NSR для покращення результатів відновлення. Мале значення NSR value посилює шум – рисунок 5.4 є)

         wnr6 = deconvwnr(blurredNoisy,PSF,NSR/2);

         figure, imshow(wnr6);

    На останньому кроці покращення результатів відновлення зображення застосуємо автокореляційну функцію до шуму NCOR та до сигналу ICOR – рисунок 5.4 ж)

         NP = abs(fftn(noise)).^2;

         NPOW = sum(NP(:))/prod(size(noise)); % сила шуму

         NCOR = fftshift(real(ifftn(NP)));

         IP = abs(fftn(im2double(A))).^2;

         IPOW = sum(IP(:))/prod(size(A));

         ICOR = fftshift(real(ifftn(IP)));

         wnr7 = deconvwnr(blurredNoisy,PSF,NCOR,ICOR);

         figure, imshow(wnr7);

    <>

    е) Відновлене з NSR

    style='font-size:12.0pt'>NSR</p> <>

    є) Відновлене з NSR/2

    class=string>NSR/2</p>

    а) Вихідне зображення

    б) Розмите зображення

    в) Відновлене за допомогою PSF

    г) Розмите та зашумлене зображення

    д) Інверсна фільтрація

    ж) Застосування автокореляційної функції