4 ТЕПЛОВІ ВЛАСТИВОСТІ ТВЕРДИХ ТІЛ

4.1 Поняття про нормальні коливання граток

Атоми твердих тіл роблять складні теплові коливання біля положень рівноваги, безпосередній кількісний опис яких являє собою значні труднощі. Тому вдаються до такого методу розгляду теплових коливань кристалічних граток.

Замість того щоб вивчати індивідуальні коливання окремих частинок, розглядають їх колективний рух в кристалі як в просторово упорядкованій системі. Такий підхід заснований на тому, що внаслідок дії сил зв'язку коливання, що виникло у однієї частинки, негайно передається сусіднім частинкам і в кристалі збуджується загальний рух у формі пружної хвилі, що охоплює всі частинки кристала. Такий загальний рух може бути поданий як сукупність синусоїдальних хвиль, названих нормальними коливаннями гратки. Число різних нормальних коливань гратки рівне числу її коливальних ступенів свободи. Оскільки кристал, що складається з N атомів, є зв'язаною коливальною системою, що має 3N степені свободи, то в ньому може бути збуджено в загальному випадку 3N нормальних коливань, що розрізняються частотами, напрямом розповсюдження і т. д.

Як приклад на рис. 4.1, а показана одновимірна модель твердого тіла – лінійний ланцюжок атомів, віддалених на відстані а один від одного і здатних коливатися в одному напрямі перпендекулярно осі ланцюжка. Якщо кінці ланцюжка з’єднані так, що повинні виконуватися періодичні граничні умови, то коливання, що відповідає найнижчій частоті , відповідає виникненню хвилі з довжиною, рівною довжині ланцюжка (рис. 4.1, б; крива 1). Наступному нормальному коливанню відповідає хвиля удвічі меншої довжини (крива 2) і т. д. Очевидно, що найкоротша довжина хвилі, яка може утворитися в такому ланцюжку, рівна подвоєній відстані між атомами ланцюжка (рис. 4.1, в):

               l_min = 2a.                                   (4.1)

Їй відповідає максимальна частота , пов'язана з довжиною хвилі l_min таким співвідношенням:

               ω_max = 2pυ/ l_min = p υ/a,                         (4.2)

де υ – фазова швидкість розповсюдження коливань в ланцюжку. Ця частота є характеристикою матеріалу і, як видно з (4.2), визначається міжатомною відстанню і швидкістю розповсюдження коливань в ланцюжку (кристалі).

Для характеристики хвильових процесів зручно користуватися хвильовим вектором q, який за напрямом збігається з напрямом розповсюдження коливань і з модулем q = 2p/l. Оскільки l= υ / n, де n – частота коливань, то q=2pn / υ = ω / υ. Звідси:

               ω = q·υ.                                   (4.3)

Формулу (4.3), що виражає залежність частоти коливань від хвильового вектора, називають дисперсійною формулою, а графік цієї залежності – дисперсійною кривою (dispersive curved).

Якби фазова швидкість J, що входить в (4.3), не залежала від довжини хвилі , то була б пропорційна q і дисперсійна крива ω(q) була б прямою 1, що показана на рис. 4.1, г штриховою лінією. Цей випадок повинен реалізуватися для безперервного середовища. В ланцюжку ж, побудованому з пружно зв'язаних атомів, тобто що має дискретну структуру, короткі хвилі, яким відповідають вищі частоти коливань, розповсюджуються повільніше, ніж довгі. Інакше кажучи, для тіл з дискретною структурою повинно мати місце явище дисперсії – залежність швидкості розповсюдження коливань від довжини хвилі або, що те ж саме, від хвильового вектора . Для простого випадку лінійного ланцюжка пружно зв'язаних атомів залежність J від q виражається таким співвідношенням:

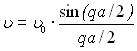          ,                              (4.4)

де υ₀ – швидкість розповсюдження низькочастотних коливань.

З (4.4) видно, що при даному значенні а швидкість практично не залежить від q і рівна приблизно тільки в області малих значень q, у якій відношення 1 у цій області ω ~ q і дисперсійна крива 2 (рис. 4.1, г) зливається з штриховою прямою для безперервного середовища. У міру ж зростання q відношення 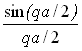зменшується, унаслідок чого зменшується і фазова швидкість розповсюдження коливань в ланцюжку (явище дисперсії). Це приводить до порушення лінійної залежності між ω і q і відхилення вниз дисперсійної кривої 2, яка в межі при q_max = ± p/a, відповідна l_min = 2a, стає паралельна осі q.

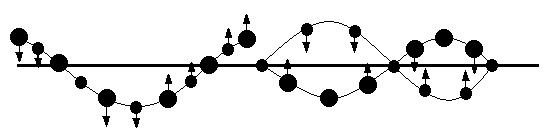
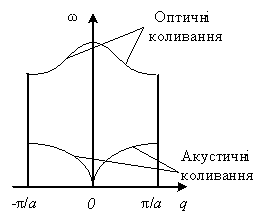
Розглянемо тепер ланцюжок, що складається з атомів двох типів, що правильно чергуються один з одним (рис. 4.2, а). Позначимо масу важчих атомів через М, легших – через m. У такому ланцюжку можливе виник-нення двох типів нормальних коливань, показаних на рис. 4.2, б, в. Коливання, показані на рис. 4.2, б, нічим не відрізняються від коливань однорідного ланцюжка: сусідні атоми коливаються практично в одній фазі і при q = 0 частота ω_ак = 0. Такі коливання називають акустичними, оскільки вони включають весь спектр звукових коливань ланцюжка. Вони відіграють основну роль у визначенні теплових властивостей кристалів – теплоємності, теплопровідності, термічного розширення і т.д.

У разі нормальних коливань, показаних на рис. 4.2, в. сусідні атоми коливаються в протилежних фазах. Ці коливання можна розглядати як коливання одне відносно одного двох підграток з однакових атомів, вставлених один в одний. Їх називають оптичними коливаннями, оскільки вони можуть збуджуватися за допомогою інфрачервоного випромінювання.

На рис. 4.2, д показані дисперсійні криві (dispersive curved) для акустичних і оптичних нормальних коливань ланцюжка, що складається з двох видів атомів. Тоді як для акустичних коливань частота росте із зростанням і досягає максимального значення при , для оптичних коливань має місце при ; із зростанням частота цих коливань зменшується і стає мінімальною при .

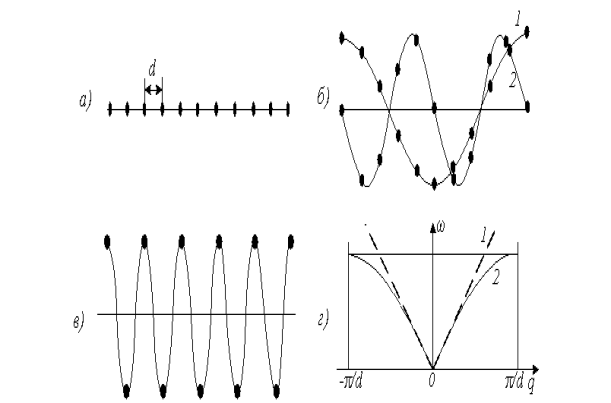
Рисунок 4.1 – Нормальні коливання лінійного ланцюжка, що складається з однакових атомів

Оптичні коливання виникають не тільки в ланцюжку, що складається з різнорідних атомів, але і у тому випадку, коли ланцюжок складається з двох і простіших ланцюжків, складених з однакових атомів і вставлених один в одного, як показано на рис. 4.2, г. В елементарній комірці такого ланцюжка міститься два атоми. Оптичні коливання (optical oscillation) виникають в результаті коливань однієї підгратки відносно іншої.

а)

б) в)

а

1 2 1 2 1 2

г)

д) е)

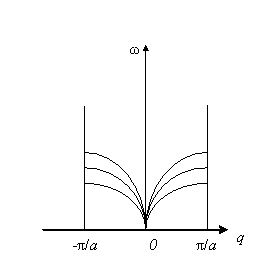
Рисунок 4.2 – Нормальні коливання ланцюжка, що складається з атомів двох типів: а) – розташування атомів в ланцюжку; б) – акустичні нормальні коливання; в) – оптичні нормальні коливання; г) – лінійна гратка з базисом; д) – дисперсійні криві для акустичних і оптичних нормальних коливань; е) – акустичні гілки нормальних коливань тривимірної гратки