4.2 Поняття про фонони

Як і лінійний гармонічний осцилятор, кожне з нормальних коливань гратки може мати тільки дискретні значення енергії. Енергія нормального коливання гратки, що має частоту рівна

     0,1,2…,                (4.5)

а спектр цього коливання повинен збігатись із спектром осцилятора. В збіганні з цим спектром мінімальна порція енергії, яку може поглинути або випустити гратка при теплових коливаннях, відповідає переходу нормального коливання з даного рівня на найближчий сусідній рівень і рівна

.                                   (4.6)

Ця порція або квант енергії теплових коливань гратки називається фононом за аналогією з квантом електромагнітного випромінювання ? фононом. Ця аналогія простежується і далі. З точки зору квантової теорії рівноважне теплове випромінювання розглядається як газ, утворений квантами світла ? фононами, що мають енергію і імпульсом , де – швидкість світла. Так само поле пружних хвиль, що заповнюють кристал, можна трактувати як газ, утворений квантами нормальних коливань ? фононами (phnton), що мають енергію і імпульс

,                         (4.7)

де ? фазова швидкість; ? довжина пружної хвилі; ? її хвильове число. З цієї точки зору кристал можна порівняти з ящиком, заповненим фононним газом.

Оскільки кристалічні гратки можуть коливатися з різними частотами , то і енергії фононів в кристалі різні. Число фононів з даною енергією визначається ступенем збудження нормального коливання з частотою . Якщо воно збуджене до n-го рівня, тобто має енергію , то говорять, що в гратці є n фононів з енергією кожний.

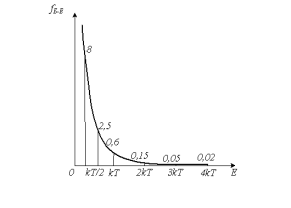
Рисунок 4.3 – Графік функції розподілу фононів за енергіями

Розподіл фононів за енергіями описується функцією Бозе ? Ейнштейна, графік якої наведений на рис.4.3. З цього графіка видно, що при температурі Т в гратці збуджені нормальні коливання практично лише до частоти ; вищих частот в гратках майже немає. Оскільки функція розподілу виражає середнє число фононів, які мають енергію , то, помноживши на одержимо середню енергію нормального коливання , збудженого в гратках при температурі і частоті :

               = ^.                    (4.8)