4.3 Теплоємність твердих тіл

Знаючи середню енергію нормального коливання (4.8), можна визначити теплову енергію гратки і її теплоємністю .

У області низьких температур (), у якій збуджуються в основному низькочастотні фонони з енергією , вираз (4.8) можна приблизно подати так:

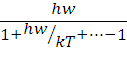
     .          (4.9)

З (4.9) витікає, що в цій області температур росте
пропорційно Т. Це зростання обумовлено збільшенням ступеня збудження кожного нормального коливання із збільшенням Т. Вважаючи, що при температурі Т в гратці збуджуються всі коливання аж до частоти , можна визначити число збуджених коливань Z:

                    . (4.10)

Таким чином, в області низьких температур енергія кристала із зростанням Т збільшується внаслідок дії двох чинників: зростання середньої енергії нормальних коливань зростання числа збуджених коливань . Тому в цілому енергія кристала росте пропорційно :

          ,                         (4.11)

а теплоємність гратки

                         (4.12)

- пропорційно що добре узгоджується з досвідом.

У області високих температур (Т>0) всі нормальні коливання гратки збуджені, тому подальше підвищення температури вже не може призводити до збільшення їх числа. Внаслідок цього в області високих температур зростання енергії твердого тіла може відбуватися тільки за рахунок підвищення ступеня збудження нормальних коливань, що викликає збільшення їх середньої енергії . Оскільки , то і зміна енерії тіла в цілому повинна бути пропорційна Т:

               ,                              (4.13)

а теплоємність тіла (heat capacity)

                    С_V                              (4.14)

не повинна залежати від Т, що також добре узгоджується з досвідом.

Одержані якісні результати можна підтвердити точнішими кількісними розрахунками.

Теплова енергія гратки

                         (4.15)

Підставляючи сюди і одержуємо

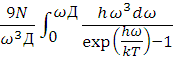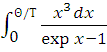= ^, (4.16)

де ; - температура Дебая.

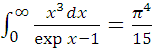Для області низьких температур () верхню межу інтеграції можна замінити Враховуючи, що одержуємо

          ,      (4.17)

          .     (4.18)

Для області високих температур і …

Підставляючи це в (4.16), знаходимо

, (4.19)

               С_V.                         (4.20)

Зокрема, для грама атома будь-якої речовини , де - число Авогадро і С_V ( - газова постійна).

Співвідношення (4.18) виражає закон Дебая, співвідношення (4.20) - закон Дюлонга і Пті. На рис. 4.4 безперервною лінією показана теоретична крива залежності теплоємності твердих тіл від температури, ділянками - експериментальні дані для ряду твердих тіл. Згода теорії з експерементом цілком задовільна.

Знаючи функцію розподілу коливань за частотами і число фононів з енергією , можна встановити залежність від Т концентрації фононового

газу, тобто числа фононів збуджених в одиниці об’єму кристала.

У області низьких температур, в якій енергія гратки Т⁴, середня енергія фонона і концентрація фононового газу повинна бути пропорційна T³.

У області високих температур, в якій Т, середня енергія фонона досягає граничного значення порядку не залежного від температури і концентрація фононового газу (background gas) повинна бути пропорційна T.

Теплоємність електронного газу. В металах крім іонів, створюючих гратку, які коливаються біля положень рівноваги, є і вільні електрони, число яких в одиниці об’єму приблизно таке ж, як і число атомів. Тому теплоємність металу повинна складатися з теплоємності гратки і теплоємності електронного газу Оцінимо порядок величини .

При нагріванні металу до температури Т термічному збудженню піддається електронів. Кожний збуджений електрон набуває в середньому енергію рівну 3/2 kT. Помноживши її на число збуджених електронів, одержимо зміну в енергії електронного газу Е_ел, обумовлене нагріванням його до температури Т:

^.

Теплоємність такого газу

.          (4.21)

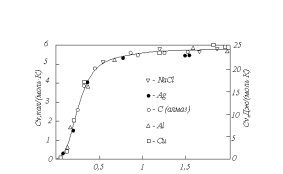
Рисунок 4.4 – Температурна залежність теплоємності твердих тіл

Для металів m вимірюється одиницями електрон - вольт; для Т =
= 300К kT 0,025еВ. Підставляючи це в (4.21), одержуємо С_ел >> 0,01 С_гр.

Таким чином, внаслідок того, що при звичайних температурах термічному збудженню піддається лише незначна частина вільних електронів металу, теплоємність електронного газу складає одиниці відсотків від теплоємності гратки.