
5 ЕЛЕКТРОПРОВІДНІСТЬ ТВЕРДИХ ТІЛ
5.1 Природа електричної провідності твердих тіл
У відсутності електричного поля електронний газ в провіднику знаходиться в рівноважному стані і описується рівноважними функціями розподілу Фермі – Дірака fф-Д (вироджений газ) і Максвелла – Больцмана fМ-Б (невироджений газ). На рис. 5.1, а, б наведені графіки розподілу fф-Д (![]() ) і fМ-Б (
) і fМ-Б (![]() ) для випадку, коли
) для випадку, коли ![]() . Вони симетричні відносно осі ординат, що вказує на те, що кількість електронів в провіднику, які рухаються в протилежних напрямах, завжди однакова, а їх середня швидкість в будь-якому напрямі рівна нулю. Цим пояснюється той факт що в провіднику, що містить скільки завгодно велике число електронів, електричний струм у відсутності зовнішнього поля не виникає.
. Вони симетричні відносно осі ординат, що вказує на те, що кількість електронів в провіднику, які рухаються в протилежних напрямах, завжди однакова, а їх середня швидкість в будь-якому напрямі рівна нулю. Цим пояснюється той факт що в провіднику, що містить скільки завгодно велике число електронів, електричний струм у відсутності зовнішнього поля не виникає.
Встановлення рівноваги електронного газу відбувається в результаті взаємодії електронів з дефектами гратки, яка супроводжується обміном енергії і імпульсом. Такими дефектами є перш за все теплові коливання гратки (фонони) і домішкові атоми. Взаємодія приводить до розсіювання електронів і встановлення безладного руху їх в провіднику.
Дрейф електронів. При прикладенні до провідника електричного поля напруженістю ![]() у ньому виникає електричний струм, густина якого, згідно з законом Ома, пропорційна
у ньому виникає електричний струм, густина якого, згідно з законом Ома, пропорційна ![]() :
:
j=se. (5.1)
Коефіцієнт пропорційності e називають питомою електропровідністю (specific electric conductivity) провідника.
Виникнення струму в провіднику свідчить про те, що під дією поля електрони набувають направленого руху і їх функція розподілу по станах змінюється. Такий направлений рух називають дрейфом електронів (drift electron), а середню швидкість цього руху – швидкістю дрейфу vд.
Сила, діюча на електрон з боку поля е, F=-qe. Якби ця сила була єдиною, то вільний електрон рухався б в провіднику весь час прискорено і швидкість його направленого руху могла б зрости до скільки завгодно великої величини навіть в полях низької напруженості. Електропровідність такого провідника була б нескінченною, а електричний опір – нульовим.
Чим же обумовлена скінченна величина електропровідності реальних провідників?
На перший погляд відповідь на це питання здається дуже простою. Адже електрони рухаються не в порожньому просторі, а в кристалі. Кристал же побудований з іонів, які мають скінченні розміри. Електрони, прискорювані полем, стикаються з іонами і тим самим гальмуються.
Проте таке пояснення є дуже примітивним. Воно засноване на уявлен-
ні про електрон як про «кульку», яка стикається з іншою «кулькою» – іоном. Але, як ми знаємо, загальний електрон це не «кулька», а швидше хвиля, делокалізована по всьому кристалу. Якщо кристал має ідеально правильну структуру (не містить дефектів), то загальний електрон вільно розповсюджується по такому кристалу – його з рівною вірогідністю можна знайти у будь-якого атома гратки. Електричний опір подібного кристала дійсно дорівнював би нулю.
Отже, справа зовсім не в тому, що електрони-кульки натрапляють на іони-кульки. Поява електричного опору пов'язана з наявністю в гратках різного роду дефектів, що спотворюють її ідеальну структуру. До таких дефектів відносяться перш за все теплові коливання гратки і домішкові атоми. Тільки взаємодія вільних електронів з цими дефектами приводить до їх розсіювання, до відновлення безладу їх руху і, як наслідок цього – до обмеження швидкості дрейфу і до скінченної величини електропровідності реальних кристалів.
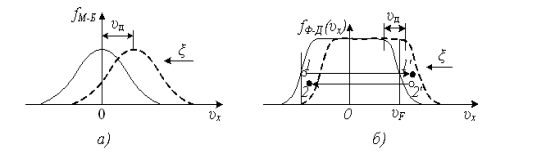
Рисунок 5.1 – Функції розподілу електронів за швидкостями для невиродженого (а) і виродженого (б) електронного газу
Вплив гратки на електрон, рухомий в ній під дією зовнішньої сили F, формально можна звести до дії сили опору Fc випробовуваної електроном, подібно кульці, рухомій у в'язкому середовищі (рис. 5.2). Ця сила пропорційна швидкості руху електрона vд і його ефективній масі тп і направлена протилежно vд:
Fc = -(1/t)mnvд, (5.2)
де 1/t – коефіцієнт пропорційності, фізичне значення якого буде з'ясовано надалі.
Використовуючи (5.2), рівняння направленого руху електрона в гратці можна записати таким чином:
mn(d vд(t)/dt) = -qe-(1/t)mnvд(t). (5.3)
З (5.3) видно, що після прикладення поля ![]() швидкість направленого руху електронів зростатиме і вони рухатимуться прискорено до тих пір, поки сила опору Fc, пропорційна vд(t), не виявиться рівною силі F=-qe, діючої з боку поля (рис. 5.2). Коли ці сили порівняються, результуюча сила, діюча на електрон, і прискорення його руху будуть рівні нулю.
швидкість направленого руху електронів зростатиме і вони рухатимуться прискорено до тих пір, поки сила опору Fc, пропорційна vд(t), не виявиться рівною силі F=-qe, діючої з боку поля (рис. 5.2). Коли ці сили порівняються, результуюча сила, діюча на електрон, і прискорення його руху будуть рівні нулю.
Починаючи з цього моменту, направлений рух електронів здійснюватиметься з постійною швидкістю дрейфу
vд=-qet/mn . (5.4)
Оскільки заряд електрона негативний, то дрейф відбувається в напрямі, протилежному e.
З'ясуємо фізичне значення t. Припустимо, що після того, як швидкість дрейфу досягла стаціонарного значення vД, поле ![]() вимкнене. Внаслідок розсіювання електронів на дефектах гратки ця швидкість почне зменшуватися і електронний газ переходитиме в рівноважний стан. Такі процеси встановлення рівноваги в системі, раніше виведеній з цього стану, називаються, як ми знаємо, релаксацією. Вважаючи на (5.3) e = 0, одержуємо рівняння, що описує перехід електронного газу в рівноважний стан – процес його релаксації
вимкнене. Внаслідок розсіювання електронів на дефектах гратки ця швидкість почне зменшуватися і електронний газ переходитиме в рівноважний стан. Такі процеси встановлення рівноваги в системі, раніше виведеній з цього стану, називаються, як ми знаємо, релаксацією. Вважаючи на (5.3) e = 0, одержуємо рівняння, що описує перехід електронного газу в рівноважний стан – процес його релаксації
dvд=(t)/dt=-(1/ t)vд(t). (5.5)
Інтегруючи (5.5), знаходимо
vд(t)= vдexp(-t/ t), (5.6)
де vд(t) – швидкість поступального руху електронів після закінчення часу ![]() після вимкнення поля.
після вимкнення поля.
З (5.5) витікає, що t характеризує швидкість встановлення в системі рівноважного стану: чим менше t, тим швидше збуджена система приходить в рівновагу. За час t = t швидкість направленого руху електронів зменшується в е раз. Час t називають часом релаксації. Він безпосередньо пов'язаний з середнім часом вільного пробігу електрона і часто ототожнюється з ним.
Рухливість носіїв. Величину, рівну відношенню швидкості дрейфу до напруженості поля, називають рухливістю носіїв (mobility carrier):
u=|vд|/e=qt/mn. (5.7)
Отже, рухливість – це дрейфова швидкість, що набувається електронами в полі одиничної напруженості.
Оцінювання показує, що для таких металів, як мідь, t >>240-3c, рухливість електронів, обчислена за формулою (5.7), і набагато більша за 340-3 м2/с, а швидкість дрейфу в полях звичайної напруженості (e>>102 В/м) vд >> 0,3 м/с. Ця величина на багато порядків нижча швидкості хаотичного руху електронів vf >>1,6![]() 10-6 м/с внаслідок чого з прикладенням поля середня швидкість електронів в провіднику залишається практично незмінною.
10-6 м/с внаслідок чого з прикладенням поля середня швидкість електронів в провіднику залишається практично незмінною.
Зручно користуватися поняттям довжини вільного пробігу електронів
l=vt, (5.8)
де v – середня швидкість руху електронів. При v = 1,6![]() 10-6 м/с і t = 240-3c з l = 240-8 що приблизно в 100 разів більше міжатомних відстаней в гратці міді. Це ще раз підтверджує той факт, що розсіювання електронів відбувається не на вузлах гратки, а на її дефектах.
10-6 м/с і t = 240-3c з l = 240-8 що приблизно в 100 разів більше міжатомних відстаней в гратці міді. Це ще раз підтверджує той факт, що розсіювання електронів відбувається не на вузлах гратки, а на її дефектах.
Питома електропровідність. Оскільки в стані теплової рівноваги середня швидкість електронів в будь-якому напрямі рівна нулю, то її можна не враховувати при обчисленні густини електричного струму і питомої електропровідності провідника, беручи до уваги тільки швидкість дрейфу електронів vд.
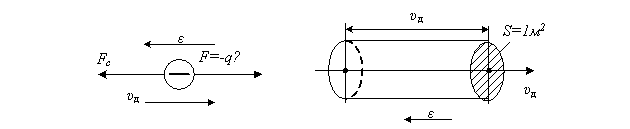
Рисунок 5.2 – Схематичне зоб-раження сил, діючих на вільний електрон провідника |
Рисунок 5.3 – До розрахунку густини струму в провіднику |
Побудуємо в об'ємі провідника циліндр з основою, рівною одиниці, і твірною, рівною vд і направленою вздовж дрейфу (рис. 5.3). Всі електрони, укладені в цьому циліндрі, протягом однієї секунди пройдуть через основу і утворять струм густиною
j=-qnvд=qnue, (5.9)
де n – концентрація електронного газу в провіднику. Порівнюючи (5.9) з (5.1), знаходимо
s=qnu![]() (5.10)
(5.10)
Підставляючи сюди і з (5.7) і ![]() з (5.8), одержуємо
з (5.8), одержуємо
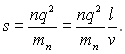 (5.11)
(5.11)
Ця формула виражає питому електропровідність провідника через мікроскопічні параметри, що характеризують електронний газ в ньому. Причому при її виведенні не робилося ніякої відмінності між невиродженим і виродженим електронним газом. Тепер спробуємо встановити, як позначається стан газу на його електропровідності.
Для невиродженого газу густина заповнення зони провідності електронами настільки мала, що на їх поведінці практично не позначається принцип Паулі. Електрони є повністю вільними в тому значенні, що на рух будь-якого з них інші не мають помітного впливу. Тому всі електрони провідності невиродженого газу беруть незалежну один від одного участь в створенні електричного струму у формуванні електропровідності провідника. Тому у вираз для електропровідності невиродженого газу повинен входити середній час релаксації (t) всіх вільних електронів, одержаний шляхом усереднення t для всієї сукупності електронів. Враховуючи це, вираз для рухливості і питомої електропровідності невиродженого газу необхідно записати таким чином:
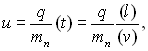 (5.12)
(5.12)
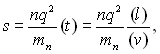 (5.13)
(5.13)
де l, v – середня довжина вільного пробігу і середня швидкість руху електронів.
Інша картина спостерігається для виродженого газу. В такому газі основна маса електронів, енергія яких менша ферміївської, не може брати участі в процесах розсіювання і змінювати стан свого руху під дією зовнішнього поля, оскільки це пов'язано з переходом електронів на сусідні рівні енергії, які повністю зайняті. Тому реагувати на зовнішнє поле можуть тільки електрони, розташовані у рівня Фермі (Ферміївські електрони). Під дією зовнішнього поля ![]() ці електрони, як показано на рис. 5.1, б, зміщуються з лівої частини розподілу в праву. При цьому зліва, звідки електрони входять, ферміївський розподіл ніби злегка «підтає», зате справа, куди приходять електрони, воно злегка «нарощується». Результуючий розподіл виглядає так, як ніби все воно зсунулося вправо, хоча насправді змінили свій стан лише ферміївські електрони. Саме за рахунок надбання ними додаткових швидкостей в зовнішньому полі і відбувається зсув розподілу.
ці електрони, як показано на рис. 5.1, б, зміщуються з лівої частини розподілу в праву. При цьому зліва, звідки електрони входять, ферміївський розподіл ніби злегка «підтає», зате справа, куди приходять електрони, воно злегка «нарощується». Результуючий розподіл виглядає так, як ніби все воно зсунулося вправо, хоча насправді змінили свій стан лише ферміївські електрони. Саме за рахунок надбання ними додаткових швидкостей в зовнішньому полі і відбувається зсув розподілу.
Як і в невиродженому газі, розсіювання носіїв приводить до хаотизації їх швидкостей і симетризації функції розподілу: коли ферміївський розподіл зміщується під дією зовнішнього поля, перекидання електронів при розсіюванні з правої частини розподілу (рис. 5.1, б) переважають над зворотними перекиданнями. В результаті сумісної дії зовнішнього поля і процесів розсіювання встановлюється деяка швидкість дрейфу носіїв
vд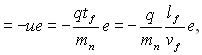 (5.14)
(5.14)
яка визначається вже не середніми значеннями t, l і v як для невиродженого газу, а часом релаксації ![]() , довжиною вільного пробігу
, довжиною вільного пробігу ![]() і швидкістю руху vF ферміївських електронів, оскільки вони обумовлюють зсув розподілу під дією поля на величину vД. З точки ж зору кількісного розрахунку провідності важливий лише сам факт зсуву розподілу електронів за швидкостями під дією поля, а не його фізичний механізм. Тому електропровідність виродженого газу як і раніше може бути записана у вигляді
і швидкістю руху vF ферміївських електронів, оскільки вони обумовлюють зсув розподілу під дією поля на величину vД. З точки ж зору кількісного розрахунку провідності важливий лише сам факт зсуву розподілу електронів за швидкостями під дією поля, а не його фізичний механізм. Тому електропровідність виродженого газу як і раніше може бути записана у вигляді
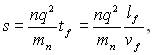 (5.15)
(5.15)
де n ? повна концентрація електронів.