|
Лабораторна робота № 6
Агрегатні методи розрахунку спектрального коефіцієнта пропускання атмосфери
Мета роботи: засвоїти практичні розрахунки коефіцієнта атмосферного пропускання та оволодіти навиками агрегатних методів розрахунку спектрального коефіцієнта пропускання атмосфери в діапазоні довжин хвиль 1…30 мкм.
6.1 Основні теоретичні відомості
6.1.1 Спектральне пропускання атмосфери без урахування розсіювання
З метою спрощення аналізу рівняння переносу випромінювання розглянемо світло, що поширюється вертикально вздовж осі z. У цьому випадку значення коефіцієнта послаблення
 враховуємо рівним одиниці. Розв’язки диференціального рівняння для плоскої земної поверхні мають вигляд (штрихами позначені змінні інтегрування) враховуємо рівним одиниці. Розв’язки диференціального рівняння для плоскої земної поверхні мають вигляд (штрихами позначені змінні інтегрування)
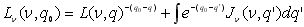 . (6.1) . (6.1)
У цьому виразі
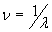 – хвильове число, см-1;
λ – довжина хвилі, см;
Lν(ν,q0) – спектральна енергетична яскравість, Вт/см2.ср у точці спостереження (z = 0);
Lν(ν,q) – спектральна енергетична яскравість у точці знаходження об’єкта (z = z); (q0 – q) – оптична товщина;
Jν(ν,q) – функція джерела. – хвильове число, см-1;
λ – довжина хвилі, см;
Lν(ν,q0) – спектральна енергетична яскравість, Вт/см2.ср у точці спостереження (z = 0);
Lν(ν,q) – спектральна енергетична яскравість у точці знаходження об’єкта (z = z); (q0 – q) – оптична товщина;
Jν(ν,q) – функція джерела.
У точці спостереження вплив розсіяного сонячного світла вважаємо вторинною причиною ослаблення випромінювання. Розсіювання від джерел, які знаходяться поза трасою, виключаємо.
На трасі з початковою точкою z1 і кінцевою z2, розташованою вище (з відповідними значеннями оптичної товщини цих точок q1 і q2), коефіцієнт пропускання, за визначенням, виражається формулою
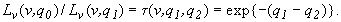 (6.2) (6.2)
Звідси випливає, що вираз під інтегралом рівняння (6.1) є еквівалентним
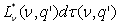 , тому одержуємо , тому одержуємо
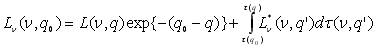 . (6.3) . (6.3)
Оскільки розв’язок інтегрального рівняння (6.3) не вдається записати у єдиній закінченій аналітичній формі, застосовуємо чисельне інтегрування. У наведеному нижче рівнянні Lνспост позначає яскравість у пункті спостереження на висоті z0 . Земну поверхню вважають плоскою, а шари атмосфери над нею однорідними (рис. 6.1). Рисунок ілюструє випадок, коли z0 = 0. Шари розділені межами z1, z2, zn . Умовно вважаємо, що спостерігач дивиться вертикально вгору на об'єкт, який знаходиться на межі zn.
У чисельній формі рівняння (6.3), відповідно до рисунка, запишемо у вигляді
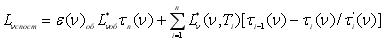 . (6.4) . (6.4)
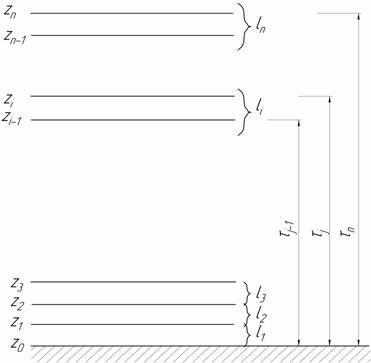
Рисунок 6.1 – Схематичний поділ атмосфери на шари
Другий член правої частини рівняння (6.4) являє собою випромінювання атмосфери у місці приймання внаслідок світла, що випускається кожним шаром та перетворюється за рахунок коефіцієнта пропускання атмосфери між приймачем і нижньою межею шару. Коефіцієнт пропускання враховує як поглинання, так і розсіювання середовища. Варто враховувати, що в рівнянні (6.4) функція джерела у i-му шарі є результатом випромінювання без урахування розсіювання в шарі світла від сусідніх областей поза шаром. Однак зауважимо, що насправді на коефіцієнт пропускання атмосфери нижнього випромінювального шару впливає як поглинання, так і розсіювання [9].
Розв’язати рівняння (6.4) при заданому
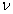 , якщо відомі величини , якщо відомі величини
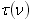 . .
Щоб з’ясувати, що можна визначити за результатами вимірів яскравості об'єкта спектрометром з даною шириною спектральної щілини (тобто спектральним інтервалом з ефективною шириною
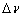 ), потрібно розрахувати ), потрібно розрахувати
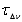 . Типова величина . Типова величина
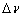 має порядок 10 см-1 або більше. має порядок 10 см-1 або більше.
Величина
 розраховується за формулою розраховується за формулою
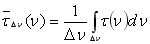 . (6.5) . (6.5)
Формула (6.5) являє собою апроксимацію з двох точок зору. По-перше, оскільки порівняння із реальними спектрометрами потребує, щоб спектральне пропускання розраховувалося для реальної ширини щілини, рівняння (6.5) варто було б насправді писати у вигляді згортки спектрального коефіцієнта пропускання із нормованою спектральною функцією щілини спектрометра (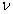 – центр інтервалу) – центр інтервалу)
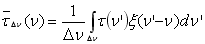 . (6.6) . (6.6)
По-друге, зміну спектра джерела у інтервалі
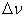 , на випромінювання якого впливає поглинання, необхідно вважати повільною. Таким чином, розглядаючи випромінювання сірих тіл, для урахування поглинання в атмосфері можна використовувати формулу (6.5), а у випадку випромінювання гарячих газів, спектральна структура яких в часі є швидкозмінною та зазвичай тісно зв'язаною зі спектром атмосфери, застосування формули (6.5) може призвести до значних похибок. Вважаємо, що джерела випромінювання мають постійний спектр, якщо відсутні інші припущення, які дозволяють використовувати рівняння (6.5) як апроксимацію. , на випромінювання якого впливає поглинання, необхідно вважати повільною. Таким чином, розглядаючи випромінювання сірих тіл, для урахування поглинання в атмосфері можна використовувати формулу (6.5), а у випадку випромінювання гарячих газів, спектральна структура яких в часі є швидкозмінною та зазвичай тісно зв'язаною зі спектром атмосфери, застосування формули (6.5) може призвести до значних похибок. Вважаємо, що джерела випромінювання мають постійний спектр, якщо відсутні інші припущення, які дозволяють використовувати рівняння (6.5) як апроксимацію.
Таким чином, усі вирази усереднюються в межах інтервалу
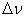 , а точність результатів залежить від точності обчислення коефіцієнта пропускання, обумовленого поглинанням , а точність результатів залежить від точності обчислення коефіцієнта пропускання, обумовленого поглинанням
 (6. 7) (6. 7)
де
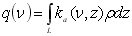 . .
6.1.2 Концепції смугової моделі
Більшість практичних підходів до розрахунку атмосферного поглинання полягає у використанні наближеної математичної моделі смугової структури спектра. При цьому вважається, що положення ліній та інтенсивність смуг можуть бути подані однією з таких математичних моделей.
1. Модель Ельзасера, побудована в припущенні, що лінії рівної інтенсивності розташовані на рівних відстанях і мають однакову півширину. Функція пропускання усереднюється за інтервалами, що дорівнюють відстані між центрами ліній.
2. Статистична модель (модель Гуді) була спочатку запропонована для парів води; у ній вважають, що положення та інтенсивність ліній описуються ймовірнісною функцією. Статистичну модель розроблено Майєром та (незалежно від нього) Гуді.
3. Модель випадкового накладання смуг Ельзасера являє собою узагальнення моделі Ельзасера та статистичної моделі. Вважають, що певна кількість смуг Ельзасера з різними значеннями інтенсивності, напівширини та відстані між смугами накладаються одна на одну випадково.
4. Найбільш точна квазівипадкова модель , у якій інтервал усереднення може бути досить малим (у порівнянні з іншими потребує найбільшого обсягу обчислень).
Якщо припустити, що окрема спектральна лінія у однорідному поглинальному газі має лоренцівську форму, вираз для поглинання має вигляд
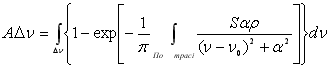 . (6.9) . (6.9)
Для однорідної траси (S,
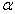 і і
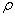 постійні) формула (6.9) спрощується постійні) формула (6.9) спрощується
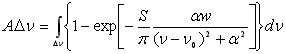 . (6.10) . (6.10)
Рисунок 6.2 – Поглинання окремою лінією залежно від частоти випромінювання (при різних кількостях поглинального агента)
Залежність поглинання від частоти для різних довжин траси і значень w наведено на рис. 6.2. Для траси довжиною z1 поглинання є малим навіть у центрі лінії. При довжині z2 випромінювання в центрі лінії поглинається повністю, і подальше збільшення z приводить тільки до зміни поглинання на краях лінії. Поглинання на трасах, довжина яких дорівнює або більше z3, розглядається як поглинання в сильній лінії [10].
Якщо припустити, що інтервал
 у (6.10) включає практично всю лінію, то без ризику внести істотну похибку межі інтегрування можна обрати від у (6.10) включає практично всю лінію, то без ризику внести істотну похибку межі інтегрування можна обрати від
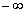 до до
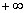 . При цьому рівняння (6.10) для визначення повного поглинання можна вирішити точно. Відповідний розв’язок має вигляд . При цьому рівняння (6.10) для визначення повного поглинання можна вирішити точно. Відповідний розв’язок має вигляд
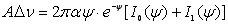 . (6.11) . (6.11)
Для поглинання у слабкій лінії розв’язок (6.11) спрощується і приймає вигляд
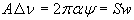 , (6.12) , (6.12)
і залежність поглинання від кількості поглинаючого агента стає лінійною.
В умовах поглинання сильною лінією
 є значним, тоді (6.12) приймає вигляд є значним, тоді (6.12) приймає вигляд
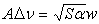 . (6.13) . (6.13)
Цей вираз відомий як наближення квадратного кореня. Наведені вище формули для окремої спектральної лінії є справедливими і для поглинання багатьма лініями за умови, якщо вони не перекриваються.
6.1.2.1 Модель Ельзасера
Ельзасерівська модель смуги поглинання формується шляхом періодичного повторення окремої лоренцівської лінії у інтервалі
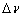 . Це приводить до ряду ліній, розташованих на однаковій відстані з постійними значеннями інтенсивності та півширини у відповідному інтервалі. Модель була запропонована Ельзасером у 1938 р. Загальний вираз для поглинання в смузі Ельзасера має вигляд . Це приводить до ряду ліній, розташованих на однаковій відстані з постійними значеннями інтенсивності та півширини у відповідному інтервалі. Модель була запропонована Ельзасером у 1938 р. Загальний вираз для поглинання в смузі Ельзасера має вигляд
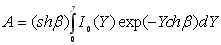 . (6.14) . (6.14)
Графік цієї функції для різних значень
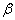 наведений на рис. 6.3. Функцію в загальному вигляді оцінити важко, тому було застосовано спроби оцінити інтеграл на основі наближених формул. Каплан розклав інтеграл у ряд, який є збіжним для значень наведений на рис. 6.3. Функцію в загальному вигляді оцінити важко, тому було застосовано спроби оцінити інтеграл на основі наближених формул. Каплан розклав інтеграл у ряд, який є збіжним для значень
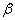 < 1,76. < 1,76.
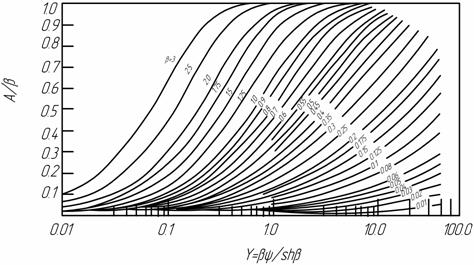
Рисунок 6.3 – Поглинання у окремій смузі Ельзасера
Наближення слабких ліній. На рис. 6.4 поглинання за формулою подано у функції добутку
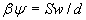 для чотирьох значень для чотирьох значень
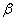 . Криві поглинання є близькими одна до одної для всіх значень w. Оскільки параметр . Криві поглинання є близькими одна до одної для всіх значень w. Оскільки параметр
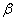 є мірою відношення ширини лінії до відстані між сусідніми лініями, спектральні лінії сильно перекриваються й окремі лінії перестають виділятися. Ця умова відповідає високим тискам, які є характерними для атмосферних трас, що проходять на невеликій висоті. Рівняння (6.14) можна апроксимувати виразом є мірою відношення ширини лінії до відстані між сусідніми лініями, спектральні лінії сильно перекриваються й окремі лінії перестають виділятися. Ця умова відповідає високим тискам, які є характерними для атмосферних трас, що проходять на невеликій висоті. Рівняння (6.14) можна апроксимувати виразом
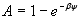 . (6.15) . (6.15)
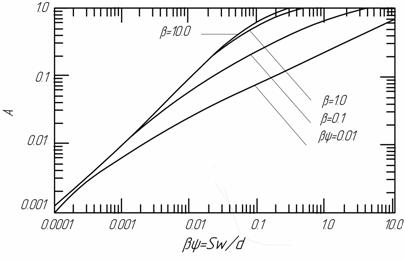
Рисунок 6.4 – Поглинання функції
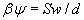 для моделі Ельзасера для моделі Ельзасера
Цей вираз є апроксимацією формули (6.14) внаслідок слабкого поглинання у центрі лінії незалежно від
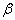 . Таку апроксимацію називають наближенням слабких ліній (воно не залежить від положення ліній усередині смуги). . Таку апроксимацію називають наближенням слабких ліній (воно не залежить від положення ліній усередині смуги).
У таблиці 6.10 зазначені області зміни
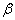 та та
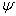 , для яких наближення слабких ліній є справедливим з точністю
≥ 10%. Апроксимація, зокрема, є корисною для екстраполяції поглинання до малих значень , для яких наближення слабких ліній є справедливим з точністю
≥ 10%. Апроксимація, зокрема, є корисною для екстраполяції поглинання до малих значень
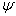 та високого тиску. Наближення слабких ліній перетворюється у лінійну апроксимацію, якщо поглинання є малим навіть при перекритті ліній. У цьому випадку та високого тиску. Наближення слабких ліній перетворюється у лінійну апроксимацію, якщо поглинання є малим навіть при перекритті ліній. У цьому випадку
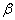 є малим, і всіма членами розкладання у ряд експоненти (6.15) можна знехтувати, за винятком члена із лінійною залежністю. є малим, і всіма членами розкладання у ряд експоненти (6.15) можна знехтувати, за винятком члена із лінійною залежністю.
Наближення сильних ліній. Протяжні атмосферні траси на великих висотах характеризуються значними кількостями w і низькими значеннями тиску
 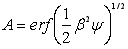 . (6.16) . (6.16)
Вираз (6.16) відомий як наближення сильних ліній смугової моделі Ельзасера.
На рис. 6.5 відповідно до (6.12) поглинання подано як функція
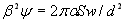 . Ця область включає велику частину потенційно важливих значень поглинання. На відміну від наближення квадратного кореня в цьому випадку лінії можуть перекриватися. Для спектральних ліній, які перекриваються, ( . Ця область включає велику частину потенційно важливих значень поглинання. На відміну від наближення квадратного кореня в цьому випадку лінії можуть перекриватися. Для спектральних ліній, які перекриваються, (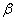 є великим) значення є великим) значення
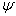 , для якого апроксимація є справедливою, обмежуються просто високим рівнем , для якого апроксимація є справедливою, обмежуються просто високим рівнем
 . Області застосування наближення сильних ліній наведені у таблиці 6.1. . Області застосування наближення сильних ліній наведені у таблиці 6.1.
Наближення ліній, що не перекриваються. Третя апроксимація у смуговій моделі Ельзасера є відомою як наближення ліній, що не перекриваються. Вона є важливою для екстраполяції поглинання до малих значень w і низьких тисків, що відповідає коротким трасам на великих висотах. За таких умов рівняння (6.14) зводиться до такого
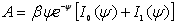 . (6.17) . (6.17)
Даний вираз збігається із поглинанням окремої спектральної лінії.
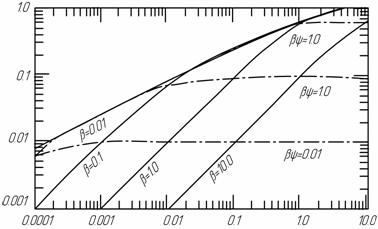
Рисунок 6.5 – Поглинання у функції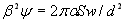 для моделі Ельзасера для моделі Ельзасера
На рис. 6.5 показана залежність відношення
 від від
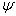 . Найвища крива є наближенням ліній, що не перекриваються. За умов . Найвища крива є наближенням ліній, що не перекриваються. За умов
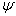 <<1 нахил кривої дорівнює 1 (область, у якій справедливим є наближення слабких ліній), а при <<1 нахил кривої дорівнює 1 (область, у якій справедливим є наближення слабких ліній), а при
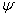 >>1 він є у 2 рази меншим (область, у якій справедливим є наближення сильних ліній). >>1 він є у 2 рази меншим (область, у якій справедливим є наближення сильних ліній).
Загальні вирази для поглинання в моделі Ельзасера (6.14) і наближенні сильних ліній (6.16) підходять для визначення поглинання, оскільки відповідні смуги складаються з регулярно розташованих ліній. Однак смуги Н2О та О3 мають тонку структуру нерегулярного характеру й не можуть бути описані рівнянням (6.14). Для виведення аналітичного виразу функції пропускання Н2О та О3 необхідно використовувати статистичні методи.
Таблиця 6.1 – Області застосування апроксимацій для смуг поглинання
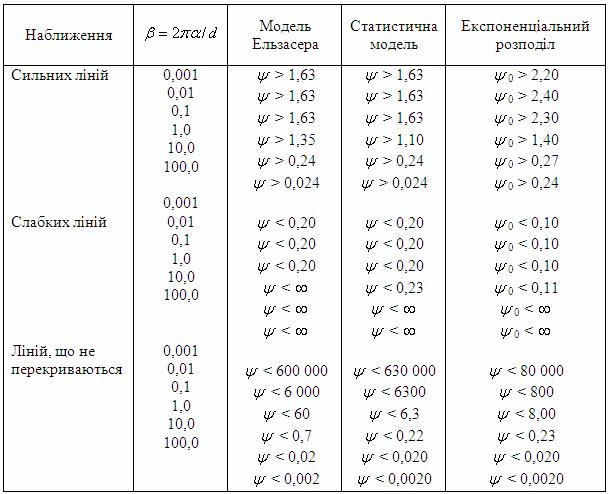
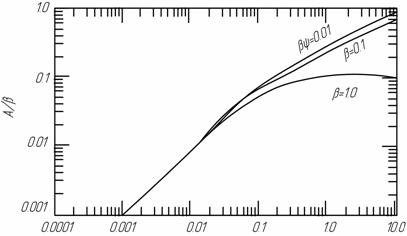
Рисунок 6.6 – Поглинання функції
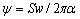 для моделі Ельзасера для моделі Ельзасера
6.1.2.2 Статистична модель
Для спектрального інтервалу
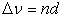 (п ліній, що знаходяться у середньому на відстані d між собою), а ймовірність того, що лінія буде мати інтенсивність від S до S + d, нормована таким чином, що (п ліній, що знаходяться у середньому на відстані d між собою), а ймовірність того, що лінія буде мати інтенсивність від S до S + d, нормована таким чином, що
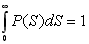 , вираз для коефіцієнта пропускання має вигляд , вираз для коефіцієнта пропускання має вигляд
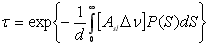 . (6.18) . (6.18)
Лінії рівної інтенсивності. Рівняння (6.18) можна оцінити для двох окремих випадків. Якщо всі лінії мають однакову інтенсивність, воно зводиться до вигляду
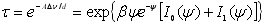 , (6.19) , (6.19)
а поглинання дорівнює
 . (6.20) . (6.20)
Якщо кожна з ліній є слабопоглинальною (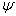 є малим), то рівняння (6.15) зводиться до є малим), то рівняння (6.15) зводиться до
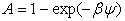 . (6.21) . (6.21)
Якщо ж лінії є поглинальними, то рівняння (6.20) приймає вигляд
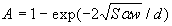 . (6.22) . (6.22)
Найбільш відомими практичними методами для розрахунку спектрального пропускання атмосфери в діапазоні довжин хвиль від 1 до 30 мкм є агрегатний метод та метод “Лоутран”.
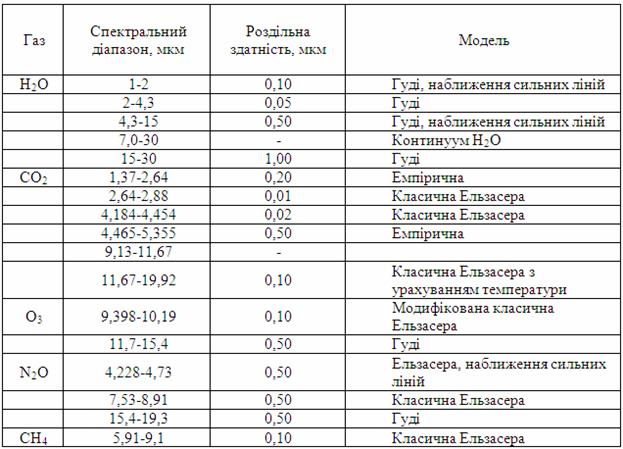
Агрегатний метод являє собою комбінацію декількох моделей. Кожна з них використовується у відповідному спектральному діапазоні, де вона забезпечує найбільш високу точність. Земна поверхня вважається плоскою, атмосфера є стандартною, однорідною вздовж горизонталі. Залежно від спектральної смуги та характерного атмосферного молекулярного поглинання речовини, у методі застосовують ряд моделей (табл. 6.2).
Таблиця 6.2 – Смугові моделі, які використовують в агрегатному методі
6.1.2.3 Агрегатний метод (модель Гуді для Н2О). Наближення сильних ліній (1,0÷2,0 мкм та 4,3÷15,0 мкм)
Коефіцієнт пропускання
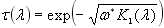 , (6.23) , (6.23)
де w* –
еквівалентна кількість поглинальної речовини
 . (6.24) . (6.24)
За відсутності вимірюваних значень величини М, Р та Т можна визначити за табл. 6.1 – 6.2 для відповідної моделі стандартної атмосфери.
6.1.2.4 Модель Гуді ( 2,0÷4,3 мкм та 15,0?÷0,0 мкм)
Коефіцієнт пропускання обчислюють за формулами:
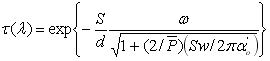 , (6.25) , (6.25)
де
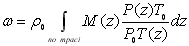 , ,
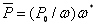 , ,
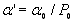 (P0=760 мм. рт. ст.). (P0=760 мм. рт. ст.).
6.1.2.5 Модель континуум Н2О (7
÷ 30 мкм)
Це область, де поглинання обумовлене Н2О та димерами Н2О, а також межами багатьох ліній, центри яких лежать поза межами континууму. Певний вплив дають також деякі лінії, центральні частоти яких лежать у межах зазначеного діапазону.
Коефіцієнт пропускання розраховують за такими формулами
 , (6.26) , (6.26)
де S – довжина горизонтальної траси (км),
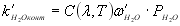 , ,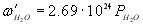 (молекула.см-2.км-1), (молекула.см-2.км-1),
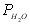 – парціальний тиск парів Н2О (атм.). – парціальний тиск парів Н2О (атм.).
При цьому
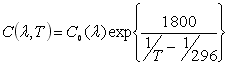 , де , де
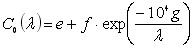 . .
Тут е = 1,25·10-22 молекула-1 см2 атм-1; g =8,30 10–3 см; f = 2,34 ? ? 10-19 молекула-1см2 атм-1.
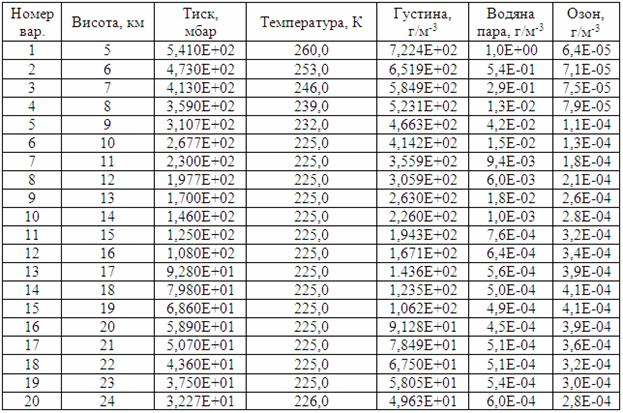
Таблиця 6.3 – Зміна властивостей атмосфери із висотою над рівнем моря
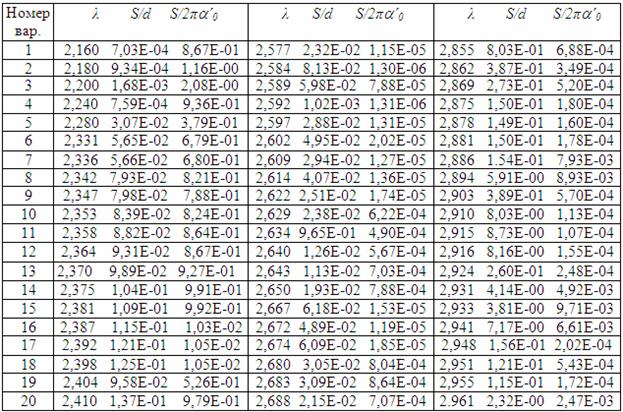
Таблиця 6.4 – Характеристики поглинання парів Н2 О (модель Гуді)
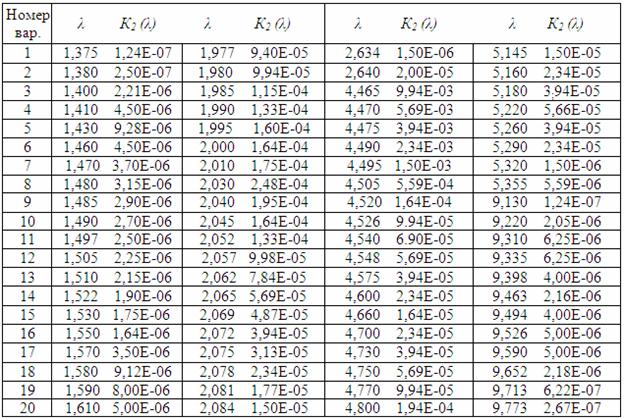
Таблиця 6.5 – Параметри поглинання у емпіричній моделі СО2
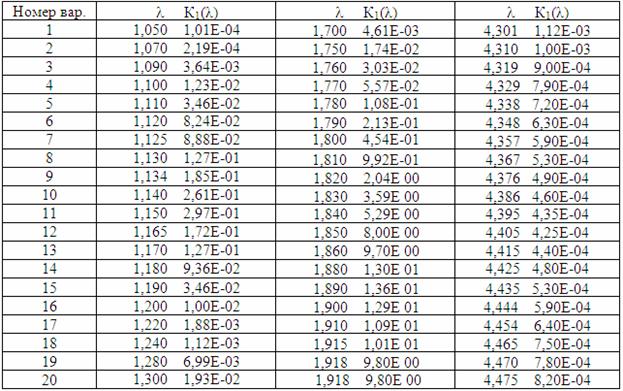
Таблиця 6.6 – Параметри поглинання парів Н2О (модель Гуді)
6.1.2.6 Емпірична модель для СО2 (1,37÷2,64 мкм; 4,65
÷5,355 мкм та 9,13
÷11,67 мкм)
Коефіцієнт пропускання
τ (λ) = [wp*
K2
(λ)]
, (6.27)
wp* =
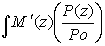 2 2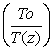 1,5dz, атм.см, 1,5dz, атм.см,
де K2(λ) – спектральний коефіцієнт (табличний); М´(z) – відношення парціального тиску поглинального газу до повного тиску. Ряд значень величини wр*K2(λ)також є табличними величинами.
6.2 Завдання та хід виконання роботи
1. Вивчити теоретичні питання, пов’язані з моделями агрегатного методу розрахунку спектрального пропускання атмосфери.
2. За моделлю Гуді у наближенні сильних ліній згідно з варіантом індивідуального завдання (таблиці 6.3, 6.6) виконати розрахунок спектрального коефіцієнта пропускання атмосфери для заданих довжин хвиль.
3. За моделлю Гуді (класичною) згідно з варіантом індивідуального завдання (таблиця 6.3, 6.4) виконати розрахунок спектрального коефіцієнта пропускання атмосфери для заданих довжин хвиль.
4. За емпіричною моделлю CO2 згідно з варіантом індивідуального завдання (таблиці 6.3, 6.5) виконати розрахунок спектрального коефіцієнта пропускання атмосфери для заданих довжин хвиль.
5. Побудувати графічні залежності
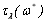 та та
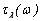 відповідно до заданих спектральних діапазонів моделей (смуг пропускання). відповідно до заданих спектральних діапазонів моделей (смуг пропускання).
Cкласти звіт.
Контрольні запитання
1. Розрахунок спектрального коефіцієнта пропускання без урахування розсіювання.
2. Концепції смугової моделі.
3. Агрегатний метод розрахунку спектрального коефіцієнта пропускання. Моделі Гуді.
4. Агрегатний метод розрахунку спектрального коефіцієнта пропускання. Емпірична модель CO2.
5. Агрегатний метод розрахунку спектрального коефіцієнта пропускання. Континуум Н2О. Статистична модель.
|