Системою числення називається сукупність цифрових знаків і правил їх з’єднання для позначення (запису) чисел. Тобто, в загальному випадку це спеціальна мова, алфавітом якої є символи, що називаються цифрами, а синтаксисом – правила, що дозволяють однозначно сформувати запис чисел.

Запис числа у будь-якій системі числення називають кодом числа. Стисло число може бути записано таким чином:

(1.1)

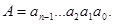
Окрему позицію у зображенні числа називають розрядом, а номер позиції – номером розряду. Число розрядів у записі числа називається розрядністю і співпадає з його довжиною.

Існує багато способів запису чисел цифровими знаками, тобто багато систем числення. В залежності від способу запису чисел і способу обчислення їх кількісного еквівалента системи числення можна класифікувати так (рис. 1.1).

У залежності від мети застосування використовуються різні системи. Наприклад, людиною для підрахунку і виконання дій над числами застосовується десяткова система числення, для обчислення часу – система обчислення часу, для нумерації – римська система числення тощо. Однак, будь-яка система числення, що призначена для практичного застосування, повинна забезпечити:

• можливість представлення будь-якого числа у заданому діапазоні чисел;

• однозначність представлення чисел;

• стислість і простоту запису чисел;

• простоту і зручність оперування числами в системі.

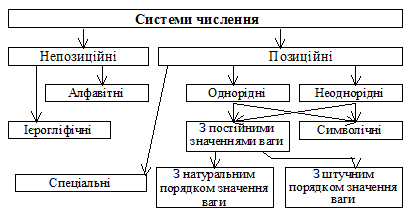
Рисунок. 1.1 – Класифікація систем числення

В основному системи числення будуються за таким принципом:

(1.2)

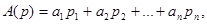
де 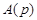– запис числа в системі із базисом 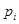, 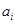– база або послідовність цифр системи числення із 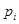-ічним алфавітом, 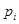– базис (основа) системи числення (сукупність значень ваг окремих розрядів системи).

База системи числення може бути додатною і змішаною. В першому випадку в ній як значення цифр використовується набір цифр 0, 1,..., (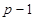). У другому випадку в системі на рівні з додатними цифрами є і від’ємні. Наприклад, для симетричної бази з нулем число додатних значень цифр дорівнює числу від’ємних. Значення цифр алфавіту в цьому випадку при р = 2t + 1 (тобто при непарній основі) становить такий ряд:

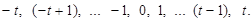
Системи числення зі змішаною базою можуть бути і при парній основі, але тоді можливо або застосування симетричних алфавітів без нуля (наприклад, при р = 2 можливий алфавіт +1, -1), або застосування алфавітів, у яких число від’ємних значень цифр не дорівнює числу додатних (наприклад, при р = 4 можливий такий алфавіт: -1, 0, 1, 2).

Основою системи числення називається кількість різних символів (цифр), що використовуються в кожному із розрядів числа для його зображення у даній системі числення.

Базис системи числення – це сукупність значень ваг окремих розрядів системи числення. Наприклад, базис десяткової системи являє собою таку послідовність: 1, 10, 10², ... 10ⁿ.

Вага розряду 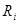числа в будь-якій системі числення – це відношення 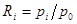. Тому цифру 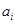розряду з великим значенням 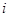називають більш значущою, ніж цифру 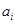розряду з меншим значенням i.

1 СИСТЕМИ ЧИСЛЕННЯ

1.1 Основні визначення. Класифікація систем числення