Попередня сторінка          Зміст           Наступна сторінка          Електронні посібники ВНТУ

1.2 Непозиційні системи числення

Непозиційними називаються такі системи числення, алфавіт яких містить необмежену кількість символів (цифр), причому кількісний еквівалент будь-якої цифри постійний і залежить тільки від її зображення, але не від позиції у записі числа. Такі системи будуються за принципом адитивності, тобто кількісний еквівалент числа визначається, як сума рядом розташованих цифр:

 

(1.3)

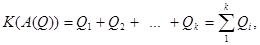
де 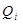 – символи, що створюють базис системи.

Найбільш відомими представниками непозиційних систем числення є ієрогліфічні та алфавітні системи числення.

Ієрогліфічні системи числення – це такі системи числення, у яких кожна цифра представлена своїм символом, значком або ієрогліфом. Найбільш відомою з них є римська система числення, у якій застосовуються, наприклад, такі значення символів:

Значення записаного числа в римській системі визначається як сума послідовно записаних цифр, наприклад, XXV = 10 + 10 + 5 = 25_(10). Якщо зліва від цифри стоїть менша цифра, то значення останньої береться зі знаком мінус, наприклад, IX = X - I = 9₍₁₀₎. Підкреслення запису числа зверху означає збільшення його у 1000 разів, наприклад, 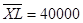. Тобто, тут існує відхилення від правила незалежності значення цифри від її розташування у числі.

Запис чисел в алфавітних системах будується за таким же принципом.

До основних недоліків непозиційних систем числення можна віднести:

•    відсутність нуля;

•    необхідність вмісту нескінченної кількості символів;

•    складність виконання арифметичних дій над числами.