Попередня сторінка          Зміст           Наступна сторінка          Електронні посібники ВНТУ

1.3 Позиційні системи числення

1.3.1 Загальні визначення

Позиційними називаються системи числення, алфавіт яких містить обмежену кількість символів, причому значення кожної цифри в числі визначається не тільки її зображенням, але і знаходиться в суворій залежності від місця її знаходження (позиції) у записі числа. Наприклад, у десятковій системі числення число 555₁₀ містить три однакові цифри, але значення кожної з них визначається її позицією, тобто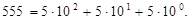 

Позиційні системи мають ряд переваг у порівнянні із непозиційними, основним з яких є зручність виконання арифметичних операцій.

У загальному вигляді число 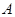 в позиційній системі числення може бути представлено таким чином:

 

(1.4)

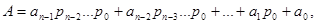
де 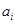  – цифра  i-го  розряду  числа, причому,  є базою системи числення, 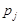 – основа системи числення,  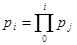–  вага i-го розряду числа.

Як видно з (1.4), такі системи будуються не тільки за принципом адитивності, але і за принципом мультиплікативності, тобто кількісний еквівалент числа визначається як сума рядом розташованих цифр зісвоєю вагою.

Позиційні системи числення, в свою чергу, поділяються на ряд підкласів (рис. 1.1).