Попередня сторінка          Зміст           Наступна сторінка          Електронні посібники ВНТУ

1.3.2 Однорідні позиційні системи числення

Однорідні позиційні системи числення є окремим випадком позиційних систем при 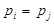 для всіх i і j, тобто в них ваги окремих розрядів являють собою ряд членів геометричної прогресії зі знаменником 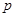. Тому число в однорідних системах може бути представлено поліномом такого виду:

 

(1.5)

або у скороченій формі:

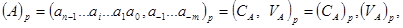
де 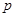-основа системи числення, 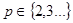,  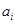– цифра і-го розряду, 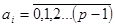,  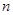– кількість цифр (розрядів) цілої частини числа,  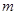– кількість цифр (розрядів) дробової частини числа.

Кома у (1.5) відділяє цілу частину 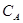 числа 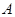 від його дробової частини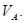 

Цифри 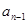 і 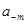 мають спеціальні назви:

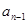•     – цифра найбільшого значення (англ. Most Signifi-cant Digit (MSD));

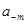•     – цифра найменшого значення (англ. Least Signifi-cant Digit (LSD)).

Очевидно, що основою однорідної позиційної системи може бути будь-яке ціле число, оскільки у визначенні позиційних систем числення не накладено ніяких обмежень на величину основи. Тому можлива нескінченна кількість однорідних позиційних систем числення, а назва системи визначає її основу: 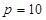– десяткова позиційна система числення, 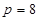– вісімкова позиційна система числення,  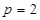– двійкова позиційна система числення  тощо.

За допомогою (1.5) можна отримати вирази для обчислення максимального значення числа 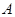. Підставимо у вираз (1.5) значення  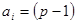і отримаємо:

 

(1.6)

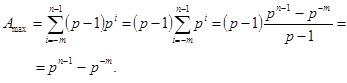
Із (1.6) видно, що значення мінімального числа, яке відрізняється від нуля, матиме такий вигляд:

 

(1.7)

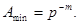
З урахуванням (1.6) і (1.7) можна визначити діапазон представлення числа 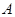  (максимальна кількість варіантів числа ):

 

(1.8)

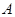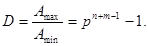
Абсолютна похибка представлення числа 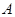 може бути визначена, як мінімальна різниця двох різних чисел:

 

(1.9)

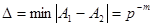
В цифрових системах найбільше розповсюдження отримали такі однорідні позиційні системи числення:

•    двійкова система числення (бінарна, англ. binary):

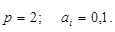
Загальна формула для запису числа у цій системі числення матиме вигляд:

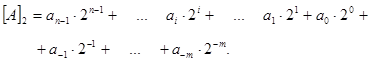
Ваги розрядів, рухаючись вліво від коми, дорівнюють відповідно 1, 2, 4, 8, 16, ..., а вправо від коми – 1/2, 1/4, 1/8 ...

Наприклад, двійкове число 110010,101₂ відповідає такому представленню у десятковій системі числення:

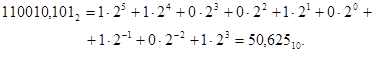
•    вісімкова система числення (октавна, англ. octal):

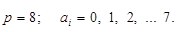
Загальна формула для запису числа у цій системі числення матиме вигляд:

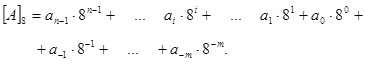
Ваги розрядів, рухаючись вліво від коми, дорівнюють відповідно 1, 8, 64, 256,  ..., а вправо від коми – 1/8, 1/64, 1/256 ... .

Наприклад, вісімкове число 317,25₈ відповідає такому представленню у десятковій системі числення:

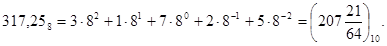
•    десяткова система числення (децимальна, англ. decimal):

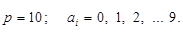
Загальна формула для запису числа у цій системі числення буде така:

 

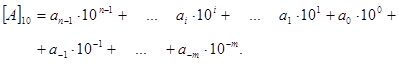
Ваги розрядів, рухаючись вліво від коми, дорівнюють відповідно 1, 10, 100, ..., а вправо від коми – 1/10, 1/10, ... .

•    шістнадцяткова система числення (гексагональна, англ. hexadecimal):

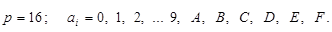
Загальна формула для запису числа, при цьому, матиме вигляд:

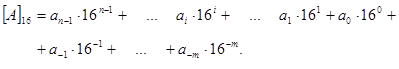
Ваги розрядів, рухаючись вліво від коми, дорівнюють відповідно 1, 16,  256, ..., а вправо від коми – 1/6,  1/256 ... .

Наприклад, шістнадцяткове число А7В,С8₁₆ відповідає такому представленню у десятковій системі числення:

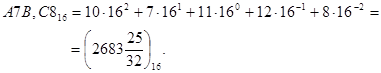
Із розглянутого видно, що вага i-го розряду 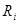 числа у позиційній системі числення являє собою відношення 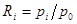. Якщо розряд має вагу, наприклад, 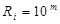, то наступний старший розряд має вагу  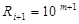, а молодший ‒ 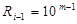. Такий взаємозв’язок розрядів вимагає передачі інформації між ними при виконанні арифметичних операцій (перенесень при додаванні та позик при відніманні).

В таблиці 1.1 наведені представлення шістнадцяти перших десяткових цифр у вказаних системах числення.