Попередня сторінка          Зміст           Наступна сторінка          Електронні посібники ВНТУ

1.3.3 Неоднорідні позиційні системи числення

У неоднорідних позиційних системах числення 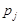 не залежить один від одного і може набувати будь-яких значень (ці системи ще називають системами зі змішаною основою).

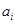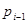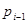У неоднорідних системах числення в кожному i-му розряді кількість допустимих символів може бути різна, при цьому 0 ≤< ,  де - основа системи числення в і-му розряді. Запис цілого числа в таких системах проводиться у відповідності із (1.1).

Прикладом неоднорідної позиційної системи числення може бути система обчислення часу, для якої 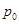 = 1 с.;  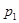= 60 c.,  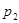= 60 хв.,  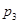= 24 год.,  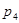= 365 діб.

Наприклад, час у 3 роки, 16 діб, 12 годин, 27 хвилин, 31 секунду в одиницях молодшого розряду, визначиться згідно з (1.2) таким чином:

Т = 3 • 365 • 24 • 60 • 1 + 16 • 24 • 60 • 1 + 12 • 60 • 1 +   +  27 • 60 • 1 +

+ 31 • 1 (секунд).

Спеціально для застосування в ЕОМ була створена неоднорідна двійково-п’ятіркова система числення, у якій в непарних розрядах основа 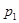 = 5 (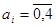), а в парних розрядах основа  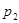= 2 ( 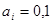). Оскільки  добуток двох сусідніх (парного і непарного) розрядів дорівнює 10, то двома двійково-п’ятірковими  розрядами можна кодувати одну десяткову цифру (табл. 1.2).

Наприклад, число 297₁₀ у двійково-п’ятірковій системі числення буде представлено так: А = 297₁₀ = (02 • 14 •12)_2-5. Тут n = 6, основи p₁ = 5; р₂ = 2; р₃ = 5; р₄ = 2; р₅ = 5; р₆ = 2, а цифри а₁ = 2; a₂ = 1; a₃ = 4; а₄ = 1; a₅ = 2; a₆ = 0. Для обчислення кількісного еквівалента числа А_2-5,  підставимо ці значення в (1.4):

А = 0 • 5 • 2 • 5 • 2• 5  + 2 • 2 • 5 • 2 • 5 + 1 • 5 • 2 • 5 + 4 • 2 • 5 +

+ 1 • 5 + 2 =  0 + 200 + 50 + 40 + 5 + 2 = 297₁₀.