Попередня сторінка          Зміст           Наступна сторінка          Електронні посібники ВНТУ

1.3.4 Кодовані позиційні системи числення

В кодованих позиційних системах числення цифри однієї системи числення кодуються за допомогою цифр іншої системи числення. Число в загальному вигляді записується таким чином:

 

(1.10)

де р – основа системи числення, символами якої кодуються числа, Р  – основа  заданої системи числення.

При побудові кодованих позиційних систем як ваги розрядів можуть бути вибрані члени геометричної прогресії (тобто ваги однорідної позиційної системи числення), а також довільні числа. У першому випадку системи називаються кодованими системами числення з природною вагою розрядів, у другому – кодованими системами числення зі штучною вагою розрядів.

Прикладом системи числення з природною вагою розрядів може бути двійково-десяткова система (англ. Dinary Coded Decimal - BCD) з вагами 8-4-2-1. У ній кожна цифра десяткового числа кодується двійковою тетрадою (чотирма двійковими розрядами). Наприклад, десяткове число 7 у двійково-десятковій системі числення матиме такий вигляд:

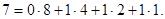
Прикладом системи числення зі штучною вагою розрядів може бути двійково-десяткова система числення з вагами 2-4-2-1. Десяткове число 7 в цій системі матиме, відповідно, такий вигляд:

.

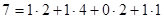Як  відомо, цей код є самодоповнюючимся, тобто в такій системі кодування десяткове число 9 кодується як 1111, що дозволяє найбільш раціонально будувати десяткові лічильники та арифметичні схеми.

Код називається самодоповнюючимся, якщо двійкові коди будь-яких двох десяткових цифр, доповнюючи одна одну до 9 (тобто якщо їх десяткова сума дорівнює 9: a'₁₀ + а''₁₀ = 9), доповнюють один одного до 15₁₀ =1111₂ (тобто їх сума a'₂ + a''₂= 1111).

Ваги розрядів у коді можуть бути не тільки додатними, але і від’ємними. Наприклад, у коді 8-4-(-2)-(-1) число 7 буде записано так:

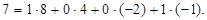
Ще одним самодоповнюючимся кодом є код 8421 плюс 3 (код з надлишком три, англ. EXCESS-3). Він отримується з природного коду 8-4-2-1 додаванням до нього числа 3₁₀ = 0011₂ за такою формулою:

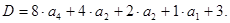
Внаслідок такого додавання отримується система з непостійною вагою розрядів. Дійсно, наприклад, цифра 1₁₀ кодується як 0100₂,  тобто в третьому двійковому розряді 1 має вагу одиниці. Тоді прикодуванні цифри 9₁₀ = 1100₂ старша двійкова цифра повинна мати вагу 8, тоді як при кодуванні цифри 5₁₀ = 1000₂ вона має вагу 5.

Відмітимо, що усі наведені коди є системами однорідними, оскільки в кожному двійковому розряді може бути дві цифри: 0 або 1.

В таблиці 1.3 наведені десяткові цифри, представлені в деяких двійково-десяткових кодах.

Необхідно підкреслитити, що двійково-десяткові коди мають певну надмірність, оскільки для кодування десяткових цифр використовується тільки 10 комбінацій із 16  можливих комбінацій, що може бути використано для виявлення деяких видів похибок.

У загальному вигляді десяткове число 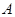, задане своїми (n + m) розрядами

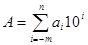
може бути представлено у двійково-десятковому коді  таким виразом:

 

(1.11)

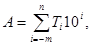
або виразом

 

(1.12)

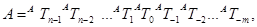
де 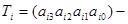і-та тетрада, ,  

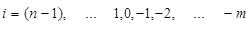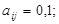
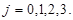
Наприклад, десяткове число А = 197₁₀ може бути записано у вказаних кодах таким чином:

•    - у коді 8421           ,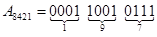

•    - у коді 2421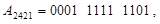                  

•    - у коді 84-2-1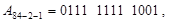      

•    - у коді 5421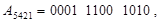            

•    - у коді 8421+3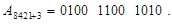    

Для кодування десяткових цифр можуть також бути використані  коди з числом розрядів, більшим за чотири (табл. 1.4).