Попередня сторінка Зміст Наступна сторінка Електронні посібники ВНТУ
1.6 Символічні системи числення
Позиційні системи числення мають чіткі і певні міжрозрядні зв’язки. Цю їх властивість можна розглядати як перевагу, оскільки вона забезпечує простоту виконання арифметичних операцій, і, разом з тим,як недолік, оскільки ця властивість через наявність міжрозрядних перенесень призводить до обмеження технічної швидкості виконання арифметичних операцій. Тому розробка непозиційних систем числення, в яких відсутні міжрозрядні зв’язки і просто здійснюються арифметичні операції, дозволила б підвищити швидкодію пристроїв для виконання арифметичних операцій.
У символічних системах, на відміну від позиційних, цифри є символами, кожен із яких окремо ніяк не характеризує будь-яке число. Певним комбінаціям цифр умовно поставлені у відповідність певні числа. Прикладами символічних систем числення є знакологарифмічна система числення і система представлення чисел у залишках або система залишкових класів (СЗК).
Головна відмінність СЗК від розглянутих вище систем полягає у тому, що в ній використовується не одна, а декілька основ:
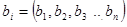 ,
,
причому і-та цифра 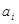 будь-якого числа
будь-якого числа 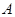 являє собою остачу від ділення заданого числа на і-ту основу
являє собою остачу від ділення заданого числа на і-ту основу 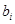 :
:
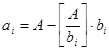
де 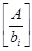 – ціла частина дробу
– ціла частина дробу 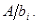
Якщо використовується одна основа 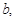 то за допомогою остач від ділення на неї однозначно можна відобразити тільки числа в діапазоні від 0 до
то за допомогою остач від ділення на неї однозначно можна відобразити тільки числа в діапазоні від 0 до 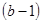 . У цьому випадку СЗК не відрізняється від звичайної позиційної системи числення з основою
. У цьому випадку СЗК не відрізняється від звичайної позиційної системи числення з основою 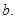 Якщо взяти дві основи
Якщо взяти дві основи 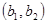 , то за допомогою остач однозначно можна відобразити числа в діапазоні від 0 до
, то за допомогою остач однозначно можна відобразити числа в діапазоні від 0 до 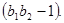 При збільшенні кількості і (або) абсолютної величини основ можна збільшити діапазон представлення чисел до необхідної величини
При збільшенні кількості і (або) абсолютної величини основ можна збільшити діапазон представлення чисел до необхідної величини 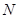 :
:
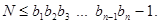
При цьому накладається умова, щоб усі 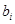 були простими числами.
були простими числами.
У таблиці 1.6 на основі виразу (1.13) наведені дворозрядні числа для п’ятнадцяти десяткових чисел, представлених в СЗК з вагою розрядів, відповідно 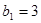 і
і 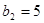 .
.
| Десяткова цифра |
СЗК |
Десяткова цифра |
СЗК |
||
| а1
( |
а2
( |
а1
( |
а2
( |
||
|
0 1 2 3 4 5 6 7 |
0 1 2 0 1 2 0 1 |
0 1 2 3 4 0 1 2 |
8 9 10 11 12 13 14 |
2 0 1 2 0 1 2 |
3 4 0 1 2 3 4 |
Із аналізу табл. 1.6 видно, що в діапазоні від 0 до 14 ні одне сполучення остач не повторюється, тобто такі сполучення остач можуть бути використані для зображення (кодування) усіх чисел в заданому виразом (1.14) діапазоні.
Із сказаного зрозуміло, що на відміну від позиційних систем числення в СЗК немає міжрозрядних зв’язків, тобто цифри у кожному розряді формуються незалежно одна від іншої.
Таким чином, усі арифметичні дії (за виключенням ділення) в СЗК є порозрядними і виконуються за простими правилами арифметики, що дозволяє спростити апаратуру для виконання операцій і збільшити її швидкодію.
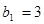 )
)