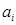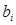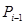Попередня сторінка          Зміст           Наступна сторінка          Електронні посібники ВНТУ

3 ДВІЙКОВА СИСТЕМА ЧИСЛЕННЯ

3.1 Загальні визначення і правила

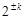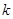Під двійковою системою числення розуміють таку систему, в якій для зображення чисел використовуються два символи, а ваги розрядів міняються згідно із законом  (де  – довільне ціле число).

Класичною двійковою системою є система з символами 0,1. Її двійкові цифри часто називають бітами.

Щоб оволодіти будь-якою системою числення, треба уміти складати і множити в ній будь-які цифри. Арифметичні операції в двійковій системі числення виконуються так само, як і в  любій позиційній системі числення з основою р відповідно до правил, розглянутих в попередньому розділі (див. табл. 2.1).

Як вже відмічалось, в загальному вигляді всі двійкові числа представляються у вигляді полінома

 

(3.1)

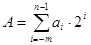
Переведення в двійкову систему числення з десяткової проводиться або за загальним правилом переведення чисел з однієї позиційної системи числення в іншу, або десяткові числа переводяться у вісімкову систему за загальним правилом, а потім вісімкові числа переводяться в двійкові за правилом переведення чисел для систем з кратною основою. Зворотний переклад проводиться аналогічно або за допомогою загального вигляду запису числа (3.1) у вигляді полінома.

Додавання у двійковій системі числення проводиться за правилами додавання поліномів. Тому при додаванні чисел Х і 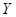 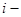й розряд суми  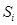 і перенесення  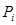 із даного розряду в 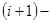й буде визначатись у відповідності із наступним правилом:

 

(3.2)

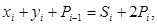
де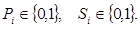 

Виразу (3.2) відповідає табл. 3.1 додавання однороз-рядних двійкових чисел. У відповідності з табл. 3.1 можна підсумовувати багаторозрядні двійкові числа.

Приклад. Задано 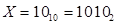 , і 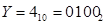. Знайти суму 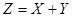. З урахуванням порозрядного додавання чисел Х і  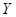отримаємо:

   ¯¯¯¯¯
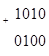