Попередня сторінка          Зміст           Наступна сторінка          Електронні посібники ВНТУ

3.2 Інші варіанти двійкової системи числення

3.2.1 Двійкова система з цифрами 1,1

З визначення двійкової системи числення витікає, що для зображення чисел можуть бути використані не тільки символи 0, 1, але і інші, наприклад, (1, -1) або (0, -1).

Символ (-1) звичайно зображають як 1, а систему, в якій використовуються символи (1,-1), називають системою (1,1). Число А = 37₁₀ запишеться, наприклад, в цій системі як А =111111, якщо вважати в (3.1), що 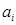 приймає значення 1 або 1.

Особливістю двійкової системи числення з цифрами 1 і 1 є представлення єдиним кодом як додатних, так і від’ємних чисел. Однак в ній відсутній нуль і немає можливості представлення деяких чисел у вигляді кінцевої множини.

У системі (1, 1) деякі цілі і дробові числа, наприклад парне (20 = 111111,111...), представляють у вигляді нескінченних дробів, тобто з певною похибкою.

Разом з тим існують числа, які не мають єдиного зображення, наприклад, число 1 може бути представлене у вигляді

 

(3.3)

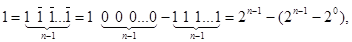
де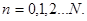 

Співвідношення (3.3) виражає зв’язок між звичайною двійковою системою числення іі системою з цифрами (1,1).

Приклад. Перевести число А = 100101 в систему (1,1). Використовуючи співвідношення (3.3), зводимо переклад до заміни комбінацій 001 і 01 комбінаціями відповідно 111 і 11, тобто А =111111.

Для отримання кінцевого представлення як парних, так і непарних чисел в системі (1,1) був запропонований наступний запис чисел:

 

(3.4)

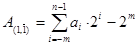
У цьому випадку через адитивну добавку додатних чисел буде менше на одне число, ніж від’ємних. Всього при 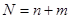 можна зобразити 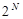чисел:  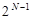від’ємних, ( 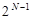– 1) додатних і нуль замість ( 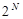– 1) чисел у двійковій системі із цифрами 0, 1, бо в останній число нуль представляється неоднозначно  (+0, -0).

Для переведення двійкових чисел в систему (1,1) існує декілька методів [ ], у більшості з яких необхідно враховувати наступне: у разі непарного числа переведення здійснюють за правилом (3.3), а потім в розряд 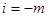записують одиницю при переведенні парного числа його спочатку перетворюють в непарне доданням одиниці в молодший розряд і тільки після цього переводять в систему (1,1) за правилом (3.3) як непарне число. Потім до отриманого результату в розряд 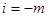записують 1.

Приклад. Перевести в систему (1, 1) двійкове число А = 11000. За вказаним правилом це число спочатку перетворюємо в непарне число 11001. Після цього замінюємо в зображенні числа комбінацію 001 на комбінацію 11, приписуємо в розряд після коми цифру 1 і отримуємо 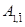= 11111,1.

Правило переведення із двійкової системи числення з цифрами 0, 1 в систему з цифрами 1,1 можна формалізувати таким чином.

Для переведення додатних чисел спочатку до початкового числа приписується праворуч ще один розряд, значення якого дорівнює 1. Після чого у початковому зображенні виділяють конструкції, що складаються із послідовності нулів і одиниці праворуч, тобто конструкції вигляду 00...01. Ці конструкції на основі (3.3) перетворюються до вигляду 11...11, тобто самий старший нульовий розряд замінюється на 1, а інші  розряди, включаючи 1 в молодшому розряді конструкції, замінюються на 1.

Приклад. Число 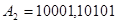 записати в системі (1,1).

Приписуємо до заданого числа праворуч розряд зі значенням 1:

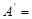 10001, 101011.

Виділяємо конструкції виду 000...01.

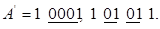
Перетворюємо виділені конструкції за правилом (3.3) і отримуємо:

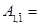 11111,  111111.

У цьому випадку доданням 1 справа до початкового запису реалізується врахування адитивної поправки. Значення цієї поправки повинне бути одне і те ж для всіх чисел, тому, якщо в початковому записі дробова частина числа має менше, ніж 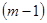  значущих цифр, то її необхідно заповнити нулями до  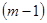розрядів і вже в 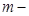й розряд записати 1.

Приклад. Число 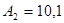  записати в системі (1,1) при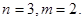   

Спочатку підготуємо запис числа до перетворення: .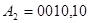

Доповнимо А розрядом справа зі значенням 1 і виділимо конструкції вигляду 00...01.

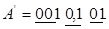
Перетворюємо виділені конструкції за правилом (3.3) і отримуємо:

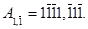
Для представлення від’ємних чисел в системі з цифрами 1,1 спочатку перетворюється запис абсолютної величини числа А шляхом дописування зліва і справа необхідного числа нулів. Потім в цьому зображенні всі 1 замінюються на 1, а до отриманого зображення дописують 1 справа (адитивна добавка). Далі виділяються конструкції вигляду 00...01 і 00...01, які перетворюються відповідно до вигляду 11...11 і. 11...11 

Приклад.  Число 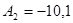 записати в системі (1,1).

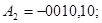
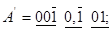
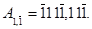
Двійкову систему числення з цифрами 1, 1  раціонально використати як проміжну при виконанні операцій множення і ділення. Пряма реалізація арифметичних дій в цій системі помітно складніша, ніж в системі з цифрами 0, 1.

Існують інші двійкові системи числення, наприклад, система із символами 1, 0, 1, яка є надмірною (надлишковою).