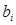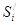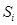Попередня сторінка Зміст Наступна сторінка Електронні посібники ВНТУ
3.2.2 Надлишкова двійкова система
Як відомо, надлишковою системою числення з основою р називається система, в якій для запису чисел використовується кількість символів, більше, ніж р.
Надлишкова двійкова (симетрична) система числення пов’язана із звичайною двійковою системою таким співвідношенням:
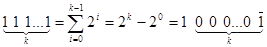
На основі виразу (3.5) проводиться перехід від двійкової системи з цифрами (0, 1) до систем з цифрами (1,0,1) і навпаки, наприклад,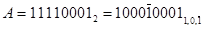 
.
У будь-якій надлишковій системі числення одні і ті ж числа можна представити декількома способами. Наприклад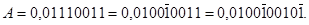 
При цьому в надлишковій системі можна зменшити кількість одиниць в зображенні числа. Симетричні надлишкові системи числення дозволяють в ряді випадків спростити виконання арифметичних дій. Наприклад, надлишкову двійкову систему числення використовують в деяких алгоритмах прискорення операції множення.
В двійковій системі числення з цифрами (1, 0, 1), як і в системі числення з цифрами (1, 1), для позначення від’ємної величини до числа не потрібно приєднувати додатковий знак, отже, при виконанні арифметичних дій над числами не потрібно використовувати ще і правила операцій із знаками. Крім того, в цій системі при виконанні операції можна уникнути поширення перенесення між розрядами далі, ніж на два (і навіть один) сусідній розряди.
Іншими словами, в цій системі за рахунок надлишковості, що вводиться, можна реалізувати методи додавання, в яких кожний розряд суми є функцією тільки суміжних справа розрядів складових величин. Це означає, що час виконання операції додавання не залежить від розрядності операндів і еквівалентний часу додавання трьох або навіть двох розрядів. Звідси витікає, що коди чисел при додаванні можуть поступати в порядку від старших розрядів до молодших, тобто починаючи зі старших розрядів.
Для доведення розглянемо наступний алгоритм додавання знакорозрядних двійкових чисел А і В.
На першому етапі проводиться порозрядне додавання операндів А і В:
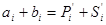
Значеннями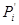 
і 
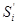можуть бути 1, 0, 1, але 
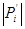= 1, якщо 
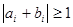(табл. 3.2).
|
|
|
|
|
|
|
|
|
|
1 1 1 0 0 0 1 1 1 |
1 0 1 1 0 1 1 0 1 |
1 1 0 1 0 1 0 1 1 |
0 1 0 1 0 1 0 1 0 |
1 1 1 0 0 0 1 1 1 |
1 0 1 1 0 1 1 0 1 |
0 1 0 1 0 1 0 1 0 |
1 0 0 0 0 0 0 0 1 |
На другому етапі до отриманого значення розрядної суми 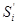додається перенесення 
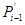із попереднього розряду:
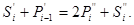
Тут вже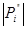 
= 1, якщо 
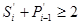(табл. 3.3).
На третьому етапі додаються значення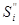 
і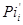 
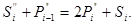
Нехай це підсумовування здійснюється точно так само, як на другому етапі, тобто SiÎ{1, 0, 1} і 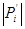= 1, якщо 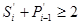. Можна показати, що при цих умовах 
.
|
|
|
|
|
|
|
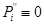2 1 0 -1 -2 2 1 0 -1 -2 |
0 0 0 0 0 1 1 1 1 1 |
1 0 0 0 0 1 1 0 0 0 |
0 0 0 1 1 0 0 0 0 1 |
0 1 0 1 0 1 0 1 0 1 |
Дійсно,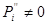 
, якщо 
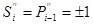. Нехай спочатку 
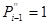, але тоді 
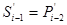. а раз 
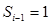, то обов’язково повинне бути 
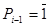. Це, в свою чергу, приводить до того, що 
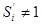(див. табл. 3.2). Также само доводиться, що 
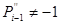; отже, 
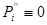і тоді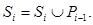 
Таким чином, при додаванні знакорозрядних двійкових операндів перенесення може розповсюджуватися не більш ніж на два розряди і, отже, максимальний час підсумовування операндів довільної розрядності становить не більше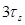 
, вважаючи, що в кожному онорозрядному суматорі час ts, формування суми більший, ніж час 
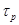формування перенесення.
Для перенесення допустимими значеннями були 1, 0, 1. Можна вважати, що при додаванні використовуються два типи перенесень додатній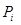
зі значеннями 0, 1 і від’ємний 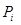зі значеннями 0, 1. Принаявності двох типів перенесень можна перебудувати алгоритм підсумовування таким чином. Спочатку знаходять суму ai, bi і додатнього перенесення з попереднього розряду 
:
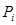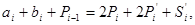
де для Si допустимі значення 0, 1 (табл. 3.3). Потім отримане значення розрядної суми S'i уточнюється шляхом додавання до неї від’ємного перенесення з попереднього розряду:
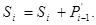
Очевидно, що при такому додаванні перенесення бути не може. Хоч даний алгоритм і не приводить до прискорення додавання, бо тут перенесення також розповсюджується на два розряди, але припрактичній реалізації він може привести до менших витрат обладнання.
Для двійкової системи числення можна добитися поширення перенесеня на один розряд, якщо один операнд представити у знакорозрядній формі, а другий - у звичайній двійковій системі числення. У цьому випадку на першому етапі порозрядно підсумовуються аi і bi:
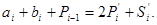
Нехай аiÎ{1, 0, 1}, а bi Î{0, 1}. Цікаво, що можна вибрати значення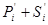 
так, що 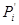Î{0, 1}, а S'i Î{0,1}. На другому етапі додаються значення 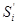і :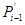
.
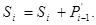Очевидно, що& при цьому ніколи не буде переповнення і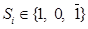 
.
Таким чином, використання знакорозрядного представлення двійкових чисел дозволяє реалізувати алгоритм додавання, при якому час виконання операції не залежить від розрядності операндів і не перевищує Зts (коли обидва операнди представлені у знакорозрядній формі) і навіть 2ts, (коли тільки один операнд представлений в знакорозрядній формі).
При множенні, на відміну від звичайної двійкової системи, утворення добутку може починатися також зі старших розрядів. У цьому випадку процес виконання операції множення може бути зупинений, коли буде отримана необхідна кількість цифр добутку, тобто досягнута необхідна точність.