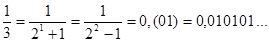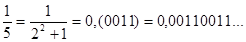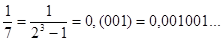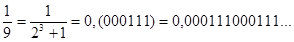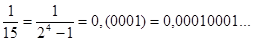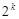Попередня сторінка Зміст Наступна сторінка Електронні посібники ВНТУ
3.2.3 Основні правила роботи з двійковими числами
Хоч усі правила виконання операцій в двійковій системі числення дуже прості, але проте при роботі з двійковими числами через відсутність навичок виникають різного роду незручності. Нижче приведенідеякі прості прийоми, які дозволяють досить вільно працювати з двійковими числами.
Правило 1. Число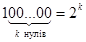 
.
Бажано знати напам’ять десяткові значення цих чисел від k = 0 хоча б до k == 12. Вони приведені в табл. 3.4.
|
|
|
|
|
|
|
|
|
|
0 |
1 |
4 |
16 |
8 |
256 |
12 |
4096 |
|
1 |
2 |
5 |
32 |
9 |
512 |
13 |
8192 |
|
2 |
4 |
6 |
64 |
10 |
1024 |
14 |
16384 |
|
3 |
8 |
7 |
128 |
11 |
2048 |
15 |
32768 |
Правило 2. Число
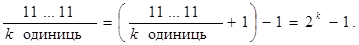
Правило 3. Бажано знати напам’ять десяткові значення двійкових чисел від 0 до 15 включно (табл. 3.5). Ці числа надалі будемо називати “малими числами".
|
Двійкове число |
Десяткове число |
Двійкове число |
Десяткове число |
|
0000 |
0 |
1000 |
8 |
|
0001 |
1 |
1001 |
9 |
|
0010 |
2 |
1010 |
10 |
|
0011 |
3 |
1011 |
11 |
|
0100 |
4 |
1100 |
12 |
|
0101 |
5 |
1101 |
13 |
|
0110 |
6 |
1110 |
14 |
|
0111 |
7 |
1111 |
15 |
Правило 4. Двійкове число
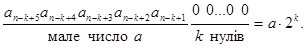
Приклади. 1101000 = 1101 • 23 =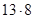 
= 104 ;
101000000 = 101 • 26 = 5 • 64 = 320.
Правило 5. Двійкове число
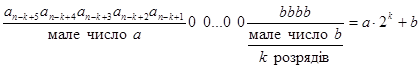
Приклади. 10110000101= 1011 • 27 + 101 =
=11 • 128 + 5 = 1413;
101000001101 = 101 • 29 + 1101 =
= 5 • 512 + 13 = 2573.
Правило 5. Читання двійкових дробів
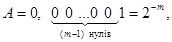
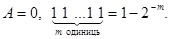
Двійковий дріб читається за тими ж правилами, що і десятковий: розряди справа від коми читаються як ціле число, яке є чисельником; знаменник читається як ціле число, що є k-им ступенем двох, причому k-номер молодшого розряду праворуч від коми.
Приклад. А = 0,11011 = 27/25 = 27/32 (читається “двадцять сім тридцять других");
А = 0,00110110 = 27/28= 54/256 (читається “п'ятдесят чотири двісті п'ятдесят шостих").
Правило 6. Двійкові дроби можуть бути періодичними. Наприклад, періодичними є дроби:
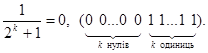
Приклади.
