Практичне заняття № 2
Мета і задачі. Основним завданням практичної роботи є набуття студентом навичок з розрахунків, проведення і підготовки приймального статистичного контролю за кількісною і якісною ознаками.
Теоретичні відомості і методичні вказівки
Приймальним контролем якості прийнято вважати сукупність заходів, проведених у процесі та після закінчення виробництва, з метою перевірки відповідності показників якості продукції встановленим вимогам.
Основне завдання приймального контролю полягає у відбраковуванні партій, кількість дефектної продукції в яких перевищує рівень, встановлений в нормативно-технічній документації для нормального ходу виробництва. В той же час під нормальним ходом виробничого процесу розуміють такий його стан, коли дотримані основні вимоги технології.
Приймальний контроль повинен бути організований таким чином, щоб більшість партій, випущених за нормального ходу виробництва, приймалися, тоді як партії з великою засміченістю дефектною продукцією, виготовлених в умовах розладженого технологічного процесу, відбраковувалися.
Поставлене завдання найбільш просто й точно може бути вирішено за допомогою так званого суцільного контролю, коли випробуванню піддається кожен виготовлений виріб. Однак у виробництві такий контроль часто неможливий: по-перше, суцільний контроль не завжди економічно виправданий, по-друге, контроль повинен бути неруйнівний, тобто виріб після контролю не повинне втрачати свої споживчі властивості.
Дослідження в області теорії ймовірностей і математичної статистики привели до висновку, що для оцінки ступеня засміченості партії дефектними виробами й ухвалення рішення про якість готової продукції немає необхідності проводити суцільну перевірку всіх виробів, а досить досліджувати лише частину партії - вибірку.
Сутність статистичного приймального контролю полягає в тому що, від партії виробів обсягом N, дотримуючись принципу випадковості, відбирають вибірку n штук, причому n, як правило, набагато менше N. Всі вироби вибірки піддаються контролю, в результаті якого визначається ступінь придатності кожного виробу для подальшого використання. Потім розраховують ті або інші характеристики, які порівнюють із нормативними. В результаті порівняння виносять рішення про її подальше використання.
Винесення правильного рішення про якість генеральної сукупності на основі результатів контролю вибірки можливо тільки тоді, коли якість вибірки відповідає якості генеральної сукупності. Така вибірка називається репрезентативною (представницькою).
Формування репрезентативної вибірки - необхідна умова вибіркового контролю. Вона відтворюється у випадку виконання таких вимог:
1) вибірка повинна бути випадковою, тобто кожен виріб з генеральної сукупності повинен мати однаковий шанс або ту саму ймовірність потрапляння у вибірку.
Досягається це різними способами. У тих випадках, коли це можливо, вироби, що входять у генеральну сукупність, ретельно перемішують і з них навмання (без розгляду) вибираються екземпляри, що включаються у вибірку. Якщо характер виробів такий, що перемішування неможливо, їх нумерують, номера переносять на картки, картки ретельно тасують і довільно вибирають із них необхідну кількість. Вироби, що відповідають номерам на картках, утворять випадкову вибірку.
Крім того, можна використовувати таблицю випадкових чисел. Вона складається з 2000 випадково розставлених цифр на кожній сторінці, кожне з яких зустрічається приблизно 200 разів. Для зручності цифри згруповані в чотиризначні числа.
При використанні таблиці випадкових чисел може виявитися, що один і той самий номер зустрічається у вибірці декілька разів. Це відповідає такому відбору карток з колоди, при якому після реєстрації номера вилученої картки вона повертається назад і перед наступним відбором карток колода знову ретельно перемішується. Така вибірка називається вибіркою з поверненням. Вона може бути організована під час послідовного відбору реальних виробів з генеральної сукупності, якщо після виконання контрольних операцій кожен виріб повертається назад і має однаковий з іншими шанс бути вибраним знову.
Якщо виріб (або картки) після відбору не повертається назад, то така вибірка називається вибіркою без повернення. За таблицею випадкових чисел вона може бути отримана за допомогою виключення повторюваних номерів.
2) вибірка повинна бути достатнього обсягу, тобто число відібраних виробів повинно бути досить великим, щоб сформувалися статистичні закономірності, характерні для генеральної сукупності. У той же час “зайві” вироби, що не роблять помітного впливу на статистичні властивості вибірки, не потрібні, тому що вони тільки збільшують невиробничі витрати.
Загальна схема приймального вибіркового контролю в спрощеному вигляді подана на рисунку 1.
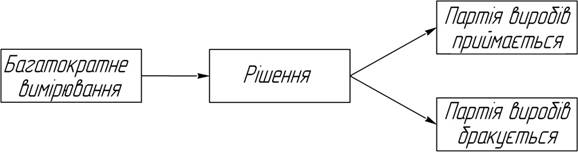
Рисунок 1 – Схема вибіркового контролю
На першому етапі контролю виконується багаторазовий вимір. Це може бути, наприклад, вимірювання якого-небудь розміру або маси виробу, що випускається серійно, будь-якого іншого параметра якості, контрольованого за шкалою відношень. Масив експериментальних даних утвориться за рахунок виміру цього параметра в кожному виробі у вибірці, так що n-кратному виміру відповідає вибірка з n виробів.
Результат багаторазового вимірювання за шкалою відношень є випадковим і підкоряється певному закону розподілу ймовірностей. На підставі його порівняння з нормативним значенням партія виробів приймається або бракується.
В іншому варіанті багаторазове вимірювання виконується за шкалою порядку. Це може бути, наприклад, вимірювання за шкалою шаблона, грубе органолептичне вимірювання або вимірювання якості експертним методом. Кожний виріб після цього визнається придатним або бракується, тому таку процедуру правильніше назвати контрольно-вимірювальною операцією.
Результат багаторазового виміру - число бракованих виробів у вибірці - є випадковим. Він підкоряється дискретному закону розподілу ймовірностей, оскільки число бракованих виробів у вибірці може бути тільки цілим. На підставі порівняння цього результату з нормою партія виробів приймається або бракується.
Для організації приймального контролю необхідно задати систему правил - план контролю, у якому вказують, як треба відбирати вироби для перевірки, після якої кількості перевірених виробів ухвалювати рішення щодо бракування або приймання партії.
Поширення одержали такі три принципи вибору плану контролю:
1) на основі даних по експлуатації виробів встановлюється припустима частка дефектності продукції q = M/N, де М - кількість дефектних виробів; N - загальна кількість виробів у партії, тобто такий граничний рівень якості, зниження якого небажано. Обсяг вибірки встановлюється таким чином, щоб при будь-якій якості продукції до контролю якість прийнятої продукції було не гірша припустимої до експлуатації;
2) відповідно до другого принципу обсяг вибірки встановлюється, виходячи з ефективності контролю і огляду на те, що подальше збільшення обсягу вибірки не приносить поліпшення вихідного рівня якості. Для використання цього принципу необхідно попередньо провести спеціальні дослідження з метою встановлення закону розподілу вихідного рівня якості. У більшості випадків як перше наближення використовується біноміальний розподіл, що вважається ідеальним для налагодженого технологічного процесу;
3) цей принцип припускає економічне обґрунтування приймального контролю. На основі аналізу процесу виготовлення й експлуатації виробів, обліку їхньої вартості, включаючи витрати на контроль, збитки від прийому дефектних виробів, установлюється обсяг вибірки N, для якого досягається максимальний ефект у порівнянні із суцільним контролем або виробництвом, в якому приймання продукції здійснюється без контролю.
На практиці одержали поширення такі види приймального контролю:
· одноступінчастий – рішення про прийняття або бракування партії приймається на підставі однієї єдиної вибірки з неї;
· багатоступінчастий – рішення про прийняття або бракування партії приймається на підставі випробувань К (2<К<7) вибірок;
· послідовний – рішення про прийняття партії, бракування або продовження випробувань приймається після оцінки кожного виробу, що перевіряється послідовно, причому число виробів, які піддаються контролю, заздалегідь не обмежено.
Подальша класифікація методів приймального контролю пов'язана із принципом класифікації результатів вимірювання. Справа в тому, що ступінь придатності виробу для подальшого використання можна визначити різними способами. Наприклад, можна реєструвати точні чисельні значення параметрів – це буде контроль за кількісною ознакою, а можна приймати одне із двох рішень: чи придатний виріб для подальшого використання чи ні, тобто ділити вироби на придатні і непридатні – контроль за альтернативною ознакою.
Оскільки під час статистичного приймального контролю судження про якість партії виноситься на підставі випробування частини виробів, то неминучі помилки, пов'язані із бракуванням якісних і прийманням неякісних партій. Під час випадкового відбору виробів можна для загальної невеликої кількості дефектних виробів у партії відібрати на перевірку значне число дефектних, що приведе до помилкового рішення про бракування придатної партії – помилка першого роду (ризик постачальника). З іншого боку, при засміченості партії дефектними виробами, у вибірці може виявитися невелика кількість дефектних, тобто неякісна партія буде прийнята – помилка другого роду (ризик споживача).
Завдання полягає в тому, щоб в умовах вибіркового контролю такі висновки робилися рідко, а ступінь їхньої можливості був заздалегідь визначений. Помилки першого й другого роду необхідно враховувати під час планування контрольних випробувань.
Для оцінки ефективності плану вибіркового контролю служить оперативна (робоча) характеристика. Під оперативною характеристикою планового контролю розуміють функцію L(q), яка рівна ймовірності прийняття партії з рівнем якості q.
Оперативна характеристика дозволяє оцінити ймовірність приймання партії для будь-якої частки дефектних виробів у партії.
За оперативною характеристикою, задаючись малою ймовірністю приймання партії (5...10)%, можна знайти відповідну частку дефектних одиниць продукції в партії або число дефектів на сто одиниць продукції. Ця величина q являє собою бракувальний рівень якості, що відповідає прийнятій ймовірності приймання (ризику споживача).
Партії із бракувальним рівнем якості будуть забраковані з високою ймовірністю (90...95)%.
За оперативною характеристикою оцінюється прийнятність вибраного плану контролю. При цьому прийнятним планом контролю для послідовності партій вважається такий, під час якого, для встановленого бракувального рівня дефектності (LQ), ризик споживача, за умови нормального рівня контролю, буде не більше заданого. Оперативні характеристики варто використовувати в тих випадках, коли потрібно вибрати план контролю для одиничної партії для встановлених приймальних і бракувальних рівнів дефектності й ризиків постачальника та споживача.
За оперативною характеристикою визначають ризик постачальника як імовірність бракування для партії з рівнем дефектності AQL, і ризик споживача як імовірність приймання для партії з рівнем дефектності LQ. Чим більша величина нахилу оперативної характеристики, тим більша строгість вибраного плану контролю.
У процесі контролю кожного виробу в партії виявляється точно відома кількість дефектних виробів. Якщо вона більша деякого критичного значення Мкр = N, то партія буде відхилена з імовірністю, рівною одиниці. Графік оперативної характеристики суцільного контролю поданий на рисунку 2.
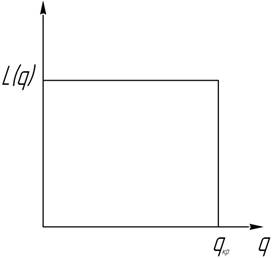
Рисунок 2 – Оперативна характеристика суцільного контролю
Оскільки на практиці неможливо побудувати таку характеристику, то постачальник і споживач домовляються про два рівні якості q0 і qm: партії з рівнем якості q < q0 вважаються свідомо придатними, а партії з рівнем якості q > qm, причому qm > q0, бракованими. Інтервал q0 < q < qm вважається зоною невизначеності. Партії з таким рівнем якості вважаються ще припустимими. Величину q0 будемо називати приймальним рівнем якості, величину qm – бракувальним рівнем якості. Оперативна характеристика плану вибіркового (статистичного) контролю подана на рисунку 3.
Таким чином, вся продукція поділяється на три рівні якості:
· продукція першої категорії – рівень якості якої становить q < q0;
· продукція другої категорії – рівень якості якої становить q > qm;
· продукція третьої категорії – рівень якості якої задовольняє співвідношення q0 < q < qm.
У кількісному співвідношенні вимоги до партії виражаються в тому, що ймовірність прийняття партії з рівнем якості q < q0 повинна бути не більша (1 – α), а імовірність приймання партії з q > qm не повинен перевищувати β. Завдання ризиків α і β забезпечувати гарантії постачальника й споживача відносно бракування якісних і приймання неякісних партій. На практиці величини α і β вибираються рівними 0,1; 0,05; 0,01. Їх величина не залежить від статистичного розрахунку, а повністю визначається наслідками від неправильно ухвалених рішень (помилок першого й другого роду).
Для будь-якого плану контролю справедливо L(q0) = 1 – α; L(qm) = β; L(1) = 0.
Ці рівняння є основою для задачі плану контролю, тобто призначення обсягу вибірки й нормативів, з якими порівнюються результати контролю, і обчислення оперативної характеристики L(q).
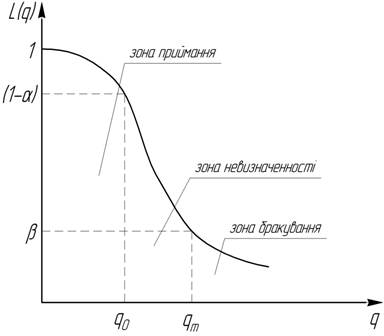
Рисунок 3 – Оперативна характеристика статистичного контролю
Величина бракувального рівня якості qm призначається, виходячи з вимог споживача, якому необхідна продукція з рівнем якості не нижче qm. Величина приймального рівня якості q0 встановлюється, виходячи з можливостей виробництва, що повинно забезпечувати випуск продукції з рівнем якості qn < q0, де qn – середній рівень засміченості партії під час нормального ходу виробництва. Тільки в цьому випадку постачальник гарантує себе від даремного бракування якісних партій, випущених з дотриманням основних вимог технології. Як правило, значення q0 трохи більше qn. В іншому випадку ефективність плану контролю знижується.
Елементи й правила комбінаторики
Комбінаторика – область математики, що вивчає питання про те, скільки різних комбінацій, які підлягають тим або іншим умовам, можна скласти із заданих об'єктів.
Можлива елементарна подія – це кожний із можливих результатів окремого випробування.
Простір елементарних подій – множина можливих елементарних подій, кожною з яких може закінчитись випробування. Якщо позначимо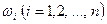 
можливі елементарні події, то цю множину можна записати у вигляді 
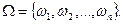Простір 
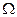може містити скінченну, зліченну або незліченну множину значень.
Сумою подій В і С називається подія А, така що А = В + С, або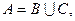 
якщо при випробуванні відбувається принаймні одна з цих подій. Множину елементарних подій, що становлять подію А, дістають об’єднанням множин елементарних подій, що становлять події В і С. Аналогічно визначається сума n (n > 2) подій.
Добутком подій В і С називається подія А, така що А = ВС, або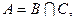 
якщо в результаті випробування відбувається як подія В, так і подія С. Множина елементарних подій, що становлять подію А, визначається як переріз множин, що становлять події В і С. Аналогічно визначається добуток n (n > 2) подій.
Різницею подій В і С називається подія А, така що А = В – С, або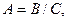 
якщо відбувається подія В і не відбувається подія С. Множина елементарних подій, що становлять подію А, містить елементарні події, що становлять В, виключаючи ті, при яких відбувається подія С.
Несумісними в даному випробуванні називаються події В і С, якщо відповідні їм множини елементарних подій не містять однакових елементів: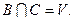 
Це означає, що коли одна з подій відбулась, друга подія відбутись не може.
Рівноможливими в даному випробуванні називаються події В і С, якщо є підстава вважати, що жодна з них не є об’єктивно більш можливою, ніж інша.
Повну групу подій у даному випробуванні утворюють події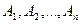 
, якщо вони несумісні і в результаті випробування неодмінно відбудеться принаймні одна з них, а отже, їхня сума є достовірною подією: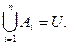 
Протилежними називаються події А і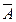 
, якщо вони несумісні й утворюють повну групу подій, тобто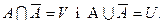 
Перестановки множини – відмінні один від одного порядком набори, складені із всіх елементів даної скінченної множини. Число перестановок множини з n визначається за формулою:
Pn = n!,
де n! = 1.2.3.… .n.
Наприклад, множина {1,2,3} має такі перестановки: (1,2,3), (1,3,2), (2,3,1), (2,1,3), (3,2,1), (3,1,2).
Розміщення з n елементів по k – упорядковані набори, що складаються з k різних елементів, вибраних з даних n елементів. Розміщення можуть відрізнятися одне від одного як елементами, так і порядком. Число розміщень їх n елементів по k визначається за формулою:
.
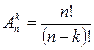Наприклад, множина {1,2,3} має такі розміщення по k = 2: (1,2), (2,1), (1,3), (3,1), (2,3), (3,2).
Сполучення – неупорядковані набори, що складаються з k елементів, узятих з даних n елементів.
Число сполучень із n елементів по k визначається за формулою:
.
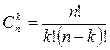Наприклад, множина {1,2,3} має сполучення по 2 елементи: (1,2), (1,3), (2,3).
Числа розміщень, перестановок і сполучень пов'язані рівністю
.
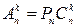Теорема додавання ймовірностей. Нехай подія А є сумою двох подій В і С. Тоді:
а) якщо події В і С несумісні, то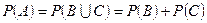 
;
б) якщо події В і С сумісні, то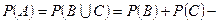 
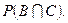
Події В і С називаються залежними, якщо ймовірність однієї з них змінюється залежно від того, відбулась друга подія чи ні. У протилежному випадку події називаються незалежними.
Імовірність події С, визначена за умови, що подія В відбулася, називається умовною і позначається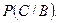 
Теореми множення ймовірностей: нехай подія А є добутком двох подій В і С. Тоді:
а) якщо події В і С незалежні, то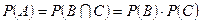 
;
б) якщо події В і С залежні, то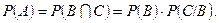 
Ці теореми справджуються й для добутку n (n > 2) подій.
Імовірність настання принаймні однієї події. Нехай у результаті випробування можуть відбутися n подій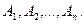 
Потрібно знайти ймовірність того, що відбудеться принаймні одна з них. Позначимо цю подію літерою А. Тоді протилежною буде подія 
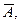яка полягає в тому, що в результаті випробування одночасно настали протилежні події: 
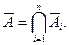Знайдемо ймовірність події А через імовірність протилежної події: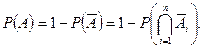 
Під час контролю якості найпоширеніші три типи розподілу дискретних випадкових величин: гіпергеометричний, біноміальний і закон Пуассона.
Гіпергеометричний розподіл. Дискретна випадкова величина Х називається розподіленою за гіпергеометричним законом, якщо її можливі значення 0,1,2,...n, а ймовірність того, що Х = d виражається формулою
,
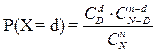де D і d – кількість дефектних одиниць продукції в партії й вибірці;
N і n – обсяг партії й вибірки.
Розрахунок імовірності того, що у вибірку обсягом n, узяту з партії обсягом N, потрапить d бракованих виробів (якщо всього їх у партії D штук), проведений за допомогою гіпергеометричного закону розподілу, відповідає визначенню ймовірності події класичним методом.
Однак обчислення, здійснювані за формулою для гіпергеометричного закону громіздкі, тому для визначення ймовірності зазвичай використовують формулу біноміального закону.
Біноміальний розподіл. Розглянемо такий випадок. У партії є N виробів (D – бракованих, N - D – придатних). Імовірність вибору придатного виробу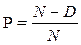 
, бракованого 
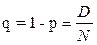. З партії беруть виріб, перевіряють його якість, після чого повертають в партію й перемішують. Потім беруть навмання інший виріб, проводять ті ж самі операції й т. д. Імовірність вибору (n - d) придатних виробів із проконтрольованих визначаються за формулою
.
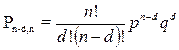Закон рідких подій (Пуассона). Закон рідких подій застосовується в машинобудуванні для вибіркового контролю готової продукції, коли з технічних умов у прийнятій партії продукції допускається деякий відсоток браку (зазвичай невеликий) – q << 0,1.
Якщо ймовірність q події А дуже мала (q ≤ 0,1), а число випробувань велике, то ймовірність того, що подія А наступить d раз в n випробуваннях, буде дорівнювати
,
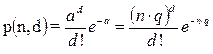де а = nq = µ[m] – математичне очікування випадкової величини.
Коли число випробувань n велике, а q мале, то закон біноміального розподілу й закон рідких подій практично збігаються. Це має місце тоді, коли q ≤ 0,1.
За допомогою закону рідких подій можна обчислити ймовірність того, що у вибірці з n одиниць буде отримуватися: 0, 1, 2, 3, і т. д. бракованих деталей, тобто задана d кількість. Можна також обчислити ймовірність появи в такій вибірці d штук дефектних деталей і більше. Ця ймовірність на підставі правила додавання ймовірностей буде дорівнювати
.
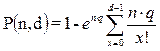Розробка плану контролю за альтернативною ознакою
Невідповідна одиниця продукції – одиниця продукції або послуга, що містить, принаймні одну невідповідність. Невідповідні одиниці продукції залежно від значимості підрозділяють на такі класи:
А – одиниця продукції, що містить одну або більше невідповідностей типажу А, може також містити невідповідності типу В і (або) С.
В – одиниця продукції, що містить одну або більше невідповідностей типажу В, може також містити невідповідності типу С, але не має невідповідностей типу А.
Відсоток невідповідних одиниць продукції – відношення числа невідповідних одиниць продукції до загального числа одиниць продукції, помножене на 100.
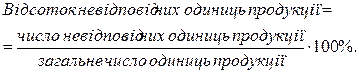
Число невідповідностей на 100 одиниць продукції – добуток частки від ділення числа невідповідностей на загальне число одиниць продукції й 100.
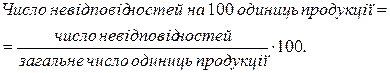
Прийнятний рівень якості (AQL) – рівень якості, що є границею задовільного середнього рівня якості процесу під час розгляду безперервної послідовності партій.
План вибіркового контролю (вибірковий план) – певний план контролю, що встановлює число одиниць продукції з кожної партії, які підлягають контролю (обсяг вибірки або обсяги серій вибірок) і необхідні критерії прийнятності партії (приймальні й бракувальні числа).
Схема вибіркового контролю (вибіркова схема) – сполучення вибіркових планів контролю й правил перемикання.
Система вибіркового контролю (вибіркова система) – сукупність вибіркових планів або схем з врахуванням обсягів партій, рівнів контролю й прийнятного рівня якості AQL.
Визначення плану контролю за альтернативною ознакою проводиться відповідно до методики затвердженої Держстандартом.
Порядок виконання і звітування
- Варіант вибирати згідно з порядковим номером по списку групи.
2. Вирішити завдання 1 за варіантами, поданими у таблиці 7.
3. Вирішити завдання 2 за варіантами, поданими у таблиці 8.
4. Вирішити завдання 3 за варіантами, поданими у таблиці 9.
5. Вирішити завдання 4 за варіантами, поданими у таблиці 10.
6. Оформити звіт з докладним розв’язанням задач.
Варіанти завдань
Завдання 1. У партії з N деталей D нестандартних. Знайти ймовірність того, що серед n узятих випадковим чином деталей d нестандартних.
Таблиця 7 – Варіанти завдань до задачі 1 практичного заняття 2
| варіант | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| N | 10 | 50 | 75 | 60 | 31 | 30 | 25 | 28 | 35 | 40 |
| D | 7 | 10 | 20 | 25 | 15 | 10 | 12 | 12 | 14 | 12 |
| n | 6 | 5 | 10 | 10 | 10 | 5 | 6 | 5 | 7 | 7 |
| d | 4 | 3 | 5 | 7 | 6 | 3 | 2 | 2 | 5 | 3 |
| варіант | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| N | 15 | 20 | 40 | 55 | 19 | 54 | 100 | 150 | 120 | 240 |
| D | 7 | 12 | 20 | 25 | 12 | 26 | 52 | 72 | 65 | 96 |
| n | 4 | 5 | 8 | 10 | 5 | 10 | 20 | 25 | 30 | 43 |
| d | 2 | 2 | 3 | 5 | 3 | 6 | 10 | 12 | 15 | 16 |
Завдання 2. За даними, наведеним у таблиці 8, для заданої бракувальної частки визначити ймовірність того, що у вибірці з поверненням серед n проконтрольованих виробів виявиться d дефектних виробів.
Таблиця 8 – Варіанти завдань до задач 2 і 3 практичного заняття 2
| варіант | q | n | d | ||
| 1 | 2 | 3 | 4 | ||
| 1 | 0,05 | 10 | 1 | ||
| 2 | 0,05 | 10 | 2 | ||
| 3 | 0,05 | 10 | 3 | ||
| 4 | 0,05 | 10 | 4 | ||
| 5 | 0,05 | 10 | 5 | ||
| 6 | 0,1 | 10 | 6 | ||
| 7 | 0,1 | 10 | 7 | ||
| 8 | 0,1 | 10 | 8 | ||
| 9 | 0,1 | 10 | 9 | ||
| 10 | 0,1 | 10 | 10 | ||
| 11 | 0,15 | 15 | 1 | ||
| 12 | 0,15 | 15 | 2 | ||
| 13 | 0,15 | 15 | 3 | ||
Продовження таблиці 8
| 1 | 2 | 3 | 4 |
| 14 | 0,15 | 15 | 4 |
| 15 | 0,15 | 15 | 5 |
| 16 | 0,2 | 15 | 6 |
| 17 | 0,2 | 15 | 7 |
| 18 | 0,2 | 15 | 8 |
| 19 | 0,2 | 15 | 9 |
| 20 | 0,2 | 15 | 10 |
Завдання 3. За даними, наведеним у таблиці 9, для відомих значень частки дефектних виробів у партії D, обсягу вибірки n, визначити ймовірності появи d дефектних виробів у вибірці.
Таблиця 9 – Варіанти завдань до задачі 3 практичного заняття 2
| варіант | q | n | d |
| 1 | 0,05 | 20 | 5, 6, 7, 8 |
| 2 | 0,07 | 30 | 4, 5, 6, 7 |
| 3 | 0,09 | 40 | 0, 1, 2, 3 |
| 4 | 0,11 | 50 | 6, 7, 8, 9 |
| 5 | 0,13 | 60 | 5, 6, 7, 8 |
| 6 | 0,15 | 70 | 4, 5, 6, 7 |
| 7 | 0,17 | 80 | 0, 1, 2, 3 |
| 8 | 0,19 | 90 | 1, 2, 3, 4 |
| 9 | 0,21 | 100 | 2, 3, 4, 5 |
| 10 | 0,23 | 120 | 3, 4, 5, 6 |
| 11 | 0,25 | 140 | 4, 5, 6, 7 |
| 12 | 0,27 | 160 | 0, 1, 2, 3 |
| 13 | 0,29 | 180 | 1, 2, 3, 4 |
| 14 | 0,31 | 200 | 2, 3, 4, 5 |
| 15 | 0,33 | 125 | 3, 4, 5, 6 |
| 16 | 0,35 | 145 | 4, 5, 6, 7 |
| 17 | 0,37 | 155 | 0, 1, 2, 3 |
| 18 | 0,39 | 175 | 1, 2, 3, 4 |
| 19 | 0,41 | 185 | 2, 3, 4, 5 |
| 20 | 0,43 | 195 | 3, 4, 5, 6 |
Завдання 4. На підприємстві машинобудівної галузі провадиться одноступінчастий контроль якості виробу за альтернативною ознакою. Визначте план контролю партії обсягом N для нормальних, ослаблених і посиленого ступенів контролю, за умови, що відомі результати суцільного контролю (кількість дефектних виробів D1, D2, D3 у партіях обсягами N1 , N2, N3, відповідно.) Вихідні дані наведені в таблиці 10. Результати роботи занесіть у таблицю 11. Інформацію для вибору коду плану контролю можна знайти за адресою в Інтернеті: http://cert.obninsk.ru/gost/1369/1369.html
Таблиця 10 – Варіанти завдань до задачі 4 практичного заняття 2
| варіант | N1 | N2 | N3 | D1 | D2 | D3 | N |
| 1 | 1000 | 900 | 1500 | 9 | 5 | 12 | 1200 |
| 2 | 700 | 500 | 1400 | 5 | 10 | 17 | 3200 |
| 3 | 500 | 1600 | 1100 | 1 | 15 | 10 | 1400 |
| 4 | 2000 | 1900 | 1700 | 18 | 15 | 14 | 2500 |
| 5 | 2000 | 1800 | 3000 | 18 | 10 | 24 | 2000 |
| 6 | 1200 | 1000 | 2000 | 10 | 7 | 15 | 1700 |
| 7 | 600 | 450 | 750 | 5 | 3 | 7 | 500 |
| 8 | 2000 | 2200 | 1800 | 15 | 16 | 10 | 1500 |
| 9 | 1000 | 1500 | 2000 | 15 | 2 | 10 | 1900 |
| 10 | 800 | 500 | 300 | 7 | 4 | 2 | 400 |
| 11 | 1200 | 800 | 300 | 11 | 7 | 5 | 500 |
| 12 | 1000 | 800 | 500 | 6 | 10 | 15 | 1500 |
| 13 | 700 | 1000 | 1200 | 6 | 10 | 9 | 1500 |
| 14 | 1200 | 1000 | 750 | 7 | 9 | 14 | 1200 |
| 15 | 2000 | 800 | 600 | 6 | 10 | 9 | 1500 |
| 16 | 2100 | 2000 | 2600 | 13 | 9 | 16 | 2000 |
| 17 | 1000 | 1200 | 1100 | 10 | 9 | 9 | 1000 |
| 18 | 1500 | 1400 | 1200 | 5 | 6 | 5 | 1100 |
| 19 | 1900 | 1700 | 1600 | 6 | 7 | 4 | 1500 |
| 20 | 2000 | 1800 | 2100 | 6 | 8 | 10 | 1900 |
Таблиця 11 – Форма подання даних розрахунку плану контролю для завдання 4
| Варіант | Рівень контролю | Прийнятний рівень якості | Об’єм контрольованої партії N | Ступінь контролю | Код об’єму вибірки | Об’єм вибірки | Критерії приймання | |
| Ас | Rc | |||||||
| Послаблений | ||||||||
| Нормальний | ||||||||
| Посилений | ||||||||
Приклад виконання
Приймальним контролем якості прийнято вважати сукупність заходів, проведених у процесі та після закінченні виробництва, з метою перевірки відповідності показників якості продукції встановленим вимогам.
Основне завдання приймального контролю полягає у відбраковуванні партій, кількість дефектної продукції в яких перевищує рівень, встановлений в нормативно-технічній документації для нормального ходу виробництва. В той же час під нормальним ходом виробничого процесу розуміють такий його стан, коли дотримані основні вимоги технології.
Приймальний контроль повинен бути організований таким чином, щоб більшість партій, випущених за нормального ходу виробництва, приймалося, тоді як партії з великою засміченістю дефектною продукцією, виготовлених в умовах розладженого технологічного процесу, відбраковувалися.
Поставлене завдання найбільш просто й точно може бути вирішено за допомогою так званого суцільного контролю, коли випробуванню піддається кожен виготовлений виріб. Однак у виробництві такий контроль часто неможливий: по-перше, суцільний контроль не завжди економічно виправданий, по-друге, контроль повинен бути неруйнівним, тобто виріб після контролю не має втрачати свої споживчі властивості.
Дослідження в області теорії ймовірностей і математичної статистики привели до висновку, що для оцінювання ступеня засміченості партії дефектними виробами й ухвалення рішення про якість готової продукції немає необхідності проводити суцільну перевірку всіх виробів, а досить досліджувати лише частину партії – вибірку. Формування такої вибірки повинно здійснюватись з дотриманням таких вимог:
1) вибірка має бути випадковою;
2) обсяг вибірки має бути достатнім для відображення статистичних закономірностей характерних для генеральної сукупності.
Задача 1. У партії з N деталей D нестандартних. Знайти ймовірність того, що серед n узятих випадковим чином деталей d нестандартних.
Розрахунок ймовірності ведеться за формулою
,
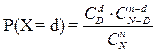де D і d – кількість дефектних одиниць продукції в партії й вибірці;
N і n – обсяг партії й вибірки.
Число сполучень із n елементів по k визначається за формулою:
,
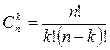N = 10, D = 7, n = 6, d = 4.
Тоді
.
.
.
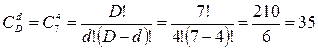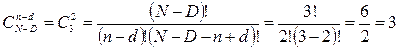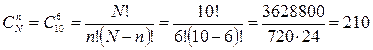Таким чином, ймовірність вибору 4 нестандартних деталей у вибірці з 6 деталей становитиме
.
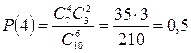Задача 2. За даними, наведеним у таблиці 8, для заданої бракувальної частки визначити ймовірність того, що у вибірці з поверненням серед n проконтрольованих виробів виявиться d дефектних виробів.
q = 0,05, n = 10, d = 1
Закон рідких подій (Пуассона). Закон рідких подій застосовується в машинобудуванні для вибіркового контролю готової продукції, коли через технічні умови у прийнятій партії продукції допускається деякий відсоток браку (зазвичай невеликий) – q << 0,1.
Якщо ймовірність q події А дуже мала (q ≤ 0,1), а число випробувань велике, то ймовірність того, що подія А наступить d раз в n випробуваннях, буде дорівнює
,
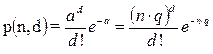де а = nq = µ[m] - математичне очікування випадкової величини.
Коли число випробувань n велике, а q мале, то закон біноміального розподілу й закон рідких подій практично збігаються. Це має місце тоді, коли q ≤ 0,1.
Згідно з формулою
.
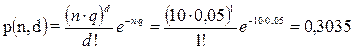Задача 3. За допомогою закону рідких подій можна обчислити ймовірність того, що у вибірці з n одиниць буде отримуватися: 0, 1, 2, 3, і т. д. бракованих деталей, тобто задана d кількість. Можна також обчислити ймовірність появи в такій вибірці d штук дефектних деталей і більше. Ця ймовірність на підставі правила додавання ймовірностей буде дорівнювати
.
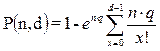q = 0,05 n = 20 d = 5,6,7,8.
Якщо d = 5, тоді
.
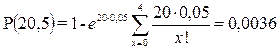Якщо d = 6, тоді
.
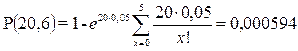Якщо d = 7, тоді
.
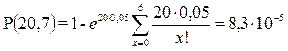Якщо d = 8, тоді
.
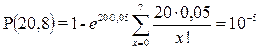Задача 4. На підприємстві машинобудівної галузі провадиться одноступінчастий контроль якості виробу за альтернативною ознакою. Визначте план контролю партії обсягом N для нормальних, ослаблених і посиленого ступенів контролю, за умови, що відомі результати суцільного контролю (кількість дефектних виробів D1, D2, D3 у партіях обсягами N1 , N2, N3, відповідно.)
| N1 | N2 | N3 | D1 | D2 | D3 | N |
| 1000 | 900 | 1500 | 9 | 5 | 12 | 1200 |
- За таблицею 1 в ГОСТ 18242-72 вибираємо коди об’єму вибірок (дані заносимо в таблицю).
- За вихідними даними розрахуємо середній приймальний рівень дефектності
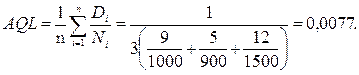
За таблицями 20-22 (ГОСТ 18242-72*) і за кодом об’єму вибираємо об’єм вибірок (дані заносимо в таблицю).
- За таблицями 20-22 (ГОСТ 18242-72*) і за кодом об’єму, об’ємом вибірки вибираємо критерії приймання (дані заносимо в таблицю 12).
Таблиця 12 – Результати розрахунку плану контролю
| Варіант | Рівень контролю | Прийнятний рівень якості AQL | Об’єм партії, що контролюється N | Ступінь контролю | Код об’єму вибірки | Об’єм вибірки | Критерії приймання | |
| Ас | Rе | |||||||
| І | Послаблений | G | 13 | 0 | 1 | |||
| Нормальний | 32 | 0 | 1 | |||||
| Посилений | 32 | 0 | 1 | |||||
| ІІ | Послаблений | J | 32 | 0 | 1 | |||
| 1 | 0,0077 | 1200 | Нормальний | 80 | 0 | 1 | ||
| Посилений | 80 | 0 | 1 | |||||
| ІІІ | Послаблений | K | 50 | 0 | 1 | |||
| Нормальний | 125 | 0 | 1 | |||||
| Посилений | 125 | 0 | 1 | |||||
Контрольні запитання
1. Дати означення таких понять:
а) ймовірність події;
б) повна група подій;
в) несумісні події;
г) рівноможливі події.
2. Дати означення теорем додавання і множення ймовірностей.
3. Які основні закони застосовуються при контролі якості за альтернативною ознакою?
4. Зобразити графіки нормальних, гіпергеометричних, біноміального законів розподілу ймовірності й графік закону розподілу ймовірності Пуассона. Описати спосіб вираження законів розподілу ймовірності у вигляді формул.
5. Якому закону розподілу ймовірності підкоряються результати контролю вибірки без повернення, вибірки з поверненням?
6. Який закон розподілу застосовується у випадку дуже малої ймовірності події?
7. Дати означення поняття «контроль якості за альтернативною ознакою».
8. Яким законам розподілу підкоряються результати контролю за альтернативною ознакою.
9. Дати означення поняття «план вибіркового контролю».
10. Яка характеристика є оцінкою ефективності плану вибіркового контролю?
11. Які фактори необхідно враховувати під час вибору рівня контролю в процесі контролю за альтернативною ознакою?
12. Які фактори необхідно враховувати під час вибору типу плану контролю в процесі контролю за альтернативною ознакою?
13. Проаналізувати плани вибіркового контролю при одноступінчастому, двоступінчастому й багатоступінчастому типах контролю й зробити висновок про зміни плану контролю під час переходу від одного до іншого типу контролю.
