---

Практичне заняття № 3

 

Мета і задачі. Аналіз Парето. АВС-аналіз. Визначення характеристик якості партії продукції. Гістограми і контрольні карти Шухарта, їх застосування.

Теоретичні відомості і методичні вказівки

Аналіз Парето

Ця діаграма названа на честь італійського економіста В. Парето, що в 1897 році, аналізуючи багатства Італії, вивів формулу, яка показує, що доходи в суспільстві розподіляються нерівномірно. Ця ж теорія в 1907 році була проілюстрована на діаграмі американським економістом                    М. С. Лоренцом. Обоє вчених показали, що в більшості випадків найбільша частка доходів (80%) належить невеликому числу людей (20%). Доктор Д. М. Джуран використовував цей постулат для класифікації проблем якості на: нечисленні істотно важливі і численні несуттєві й назвав цей метод аналізом Парето. Відповідно до цього методу в більшості випадків найбільша кількість дефектів і пов'язаних з ними матеріальних втрат виникає через відносно невелике число причин. Таким чином, з'ясувавши причини появи основних дефектів, можна усунути майже всі втрати, зосередивши зусилля на ліквідації саме цих причин. Аналіз Парето - це інструмент, що дозволяє об'єктивно показати й виявити основні фактори, що впливають на досліджувану проблему та розподілити зусилля для її вирішення.

Аналіз Парето застосовується як для виявлення проблем або гострих питань, так і для аналізу причин, що викликають ці проблеми. Тому розрізняють два види діаграм Парето: за результатами діяльності та через причину.

Аналіз Парето за результатами діяльності призначений для виявлення основної проблеми, що викликає такі небажані результати діяльності в різних напрямах:

·     якість – невідповідності, помилки, рекламації, ремонт, повернення продукції;

·     собівартість – обсяг втрат, витрати;

·     терміни поставок – недостача запасів, помилки в складанні рахунків, зриви термінів поставок;

·     безпека – нещасні випадки, аварії.

Аналіз  Парето  через  причину показує причини проблем, що виникають  у виробництві, і використовується для виявлення головної з них:

·     виконавець роботи – зміна, бригада, вік, досвід роботи, кваліфікація;

·     устаткування – верстати, оснащення, інструменти, штампи й т. д.;

·     сировина – виробник, вид сировини, партія;

·     метод роботи – умови виробництва, прийоми роботи, послідовність операцій;

·     виміри – точність, відтворюваність, стабільність, тип вимірювального приладу.

Аналіз Парето, включає такі етапи:

1. Визначення мети. Вона повинна бути сформульована точно й чітко. Має бути встановлений метод та період збору і класифікації даних.

2. Організація й проведення спостережень. Потрібно розробити контрольний листок для  реєстрації даних з переліком видів інформації, що збирається.

3. Аналіз результатів спостережень, виявлення найбільш значимих факторів. Необхідно розробити бланк таблиці для даних, передбачивши в ньому графи для підсумків з кожної перевіреної ознаки окремо, накопиченої суми числа дефектів, відсотків за загальним підсумком й накопиченими відсотками. При цьому необхідно розташувати дані, отримані з кожного фактора, у порядку значимості й заповнити таблицю. Групу «Інші» завжди записують в останній рядок.

4. Побудова діаграми, що наочно показує відносну значимість кожного із факторів. Побудуйте стовпцевий графік, де кожному виду браку відповідає  прямокутник, вертикальний рядок якого відповідає значенню суми втрат від цього виду браку (основи всіх прямокутників рівні).

5. Побудова графіка Парето. Накресліть кумулятивну криву, з'єднуючи праві кінці кожного інтервалу між собою відрізками.

При побудові діаграм Парето необхідно звертати увагу на такі моменти:

·     діаграма Парето виявляється найбільш ефективною, якщо число факторів, розташовуваних по осі абсцис, становить 7-10;

·     при обробці даних необхідно проводити їх розшарування по окремих факторах, які повинні бути добре відомі: час збору даних, тип виробів, партія сировини матеріалів або комплектуючих, процес, керівник, клієнт, верстат, оператор і т. д.;

·     при побудові діаграми Парето для конкретного числа випадків (відсотка) у випадку можливості підрахунку суми витрат варто відображати на діаграмі також і суму витрат (втрат);

·     у тому випадку, коли всі стовпці на діаграмі Парето виявляються однієї висоти, тобто різниці у внеску окремих факторів у появі браку немає, то рівномірність розподілу внеску факторів у появі браку може бути обумовлена неправильним підходом до розшарування, тому в таких випадках при розшаруванні варто перевірити дані або зібрати нові;

·     у випадку, коли фактор "Інші" виявляється занадто великим у порівнянні з іншими факторами, варто повторити аналіз змісту фактора "Інші", а також знову проаналізувати всі фактори;

·     якщо фактор, який стоїть першим, технічно важкий для аналізу, варто почати з аналізу наступного за ним;

·     якщо виявляється фактор відносно якого легко провести поліпшення, то його варто проводити, не звертаючи уваги на його місце в порядку розташування факторів у діаграмі;

·     при систематичному щомісячному складанні діаграм Парето для одного і того ж самого процесу й порівняння цих діаграм у деяких випадках, незважаючи на відсутність помітних змін загальної кількості браку, змінюють порядок розташування факторів, що впливає на появу браку. При порушенні стабільності процесу в цьому випадку нестабільність буде відразу помічена. Якщо вдасться зменшити вплив цих факторів однаковою мірою, проявиться висока ефективність поліпшення.

Після проведення вироблених на основі аналізу даних заходів звичайно проводиться повторний аналіз з метою оцінки ефективності вжитих заходів. При цьому повторюється вся процедура побудови діаграми Парето, і нові результати порівнюються з даними, отриманими раніше.

Під час використання діаграми Парето найпоширенішим методом аналізу є так званий АВС-аналіз. Тут фактори, за якими проводиться аналіз, об’єднуються в три групи А, В, С:

·     на групу А припадає 70 – 80% всіх дефектів або витрат, якщо проводиться вартісний аналіз;

·     на групу С – 5 – 10%;

·     проміжна група  В характеризується 10 - 25% витрат, які пов’язані з помилками й дефектами в роботі.

Очевидно, що в першу чергу необхідно жорстко контролювати появу дефектів, які відносяться до групи А. Необхідно піддати ретельному аналізу дані різновиди дефектів, щоб визначити причини їх появи.

Діаграму Парето доцільно застосовувати разом із причинно-наслідковою діаграмою Ісікави. Після проведення коригувальних заходів діаграму Парето можна знову побудувати для умов, що змінилися в результаті корекції, і перевірити ефективність проведення змін.

В основі будь-якого заходу повинна лежати достовірна інформація. Саме таку інформацію дозволяє одержати діаграма Парето.

 

Гістограма

Основу будь-якого дослідження становлять дані, отримані в результаті контролю й виміру одного або декількох параметрів виробу (характеристики якості). У всіх галузях промисловості потрібне проведення аналізу точності й стабільності процесу, спостереження за якістю продукції, відстеження істотних показників виробництва. Шляхом вимірювання відповідних параметрів необхідними засобами одержують ряд даних, що являють собою неупорядковану послідовність значень параметра, на основі яких неможливо зробити коректні висновки. Тому для осмислення якісних характеристик виробів, процесів, виробництва (статистичних даних) часто будують гістограму розподілу.

Гістограма - це інструмент, що дозволяє наочно оцінити розподіл статистичних даних, згрупованих за частотою влучення даних у певний (заздалегідь заданий) інтервал.

Гістограма - це стовпцева діаграма, яка використовується для графічного подання наявної кількісної інформації, зібраної за тривалий період часу (тиждень, місяць, рік і т. д.), що подає важливу інформацію для оцінки проблеми й знаходження способів її вирішення.

Гістограма застосовується головним чином для аналізу значень вимірюваних параметрів.

Загальний порядок побудови гістограми.

1.      Збираються дані контрольованого параметра (xi) за певний період  (місяць, квартал, рік і т. д.). Число даних повинно бути не менш 30 - 50, оптимальне число кратне 100.

2. Визначаються найбільше Xmax і найменше Хmin значення із всіх отриманих даних і обчислюється розмах R:

R = Xmax – Xmin.

Розмах характеризує розкид контрольованої величини, він визначає ширину гістограми.

3. Отриманий діапазон (розмах) ділиться на кілька інтервалів. Число інтервалів k залежить від загального числа зібраних даних n і деяких інших факторів. Рекомендується використовувати формулу Стерджесса:

k = 1 + 3,322 · lg(n)

4. Далі визначають ширину інтервалу:

R / k = ( Xmax - Xmin) / k.

Всі отримані дані розподіляють по інтервалах. Якщо якесь значення попадає на границю, його варто відносити до лівого стосовно неї інтервалу. Підраховується число значень, що потрапили в кожний інтервал mj, де j – номер інтервалу.

5. Для кожного інтервалу підраховується відносна частота влучення в нього даних:

.

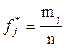6. За отриманим даними будується гістограма – стовпцева діаграма, висота стовпців якої відповідає частоті або відносній частоті влучення даних у кожний з інтервалів.

7. Обчислюють накопичену відносну частоту, додаючи кожне наступне значення відносної частоти до суми попередніх значень і будують гістограму розподілу.

 

Контрольні карти

Контрольні карти – інструмент, що дозволяє відслідковувати хід протікання процесу й впливати на нього (за допомогою відповідного зворотного зв'язку), попереджаючи його відхилення від пропонованих до процесу вимог.

У. А. Шухарт вважав, що контрольні карти повинні відповідати трьом головним вимогам.

1.  Визначати необхідний рівень або номінал процесу, на досягнення якого повинен бути націлений персонал підприємства.

2.  Використовуватися як допоміжний засіб для досягнення цього номіналу.

3.  Служити як основа для визначення відповідності номіналу й допускам. Таким чином, принципи побудови контрольних карт Шухарта охоплюють коло понять, пов'язаних зі стабілізацією виробничого процесу, його продуктивністю й оцінкою якості, а реалізація цих принципів сприяє взаємозв’язку різних напрямків господарської діяльності.

Існує два типи контрольних карт: один призначений для контролю параметрів якості, що являють собою безперервні випадкові величини, значення яких є кількісними даними параметра якості (значення розмірів, маса, електричні й механічні параметри й подібне), а другий – для контролю параметрів якості, що являють собою дискретні (альтернативні) випадкові величини і значення, які є якісними даними (придатний – не придатний, відповідає – не відповідає, дефектний – бездефектний виріб і подібне).

Залежно від виду даних і методів їх статистичної обробки виділяють різні типи контрольних карт, основні з яких подані на рисунку 8.

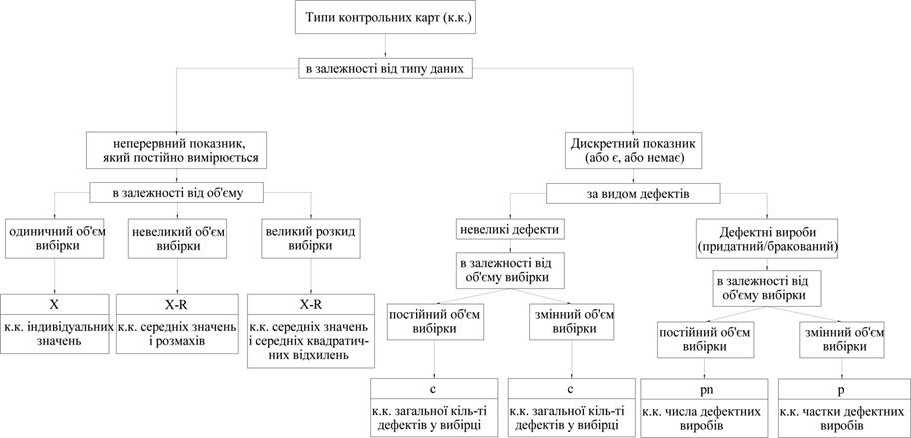
Рисунок 8 – Основні типи контрольних карт Шухарта

Найважливіше в процесі керування, так це точне розуміння стану об'єкта керування за допомогою читання контрольних карт і швидке здійснення відповідних дій, як тільки в об'єкті виявилося що-небудь незвичайне, невипадкове. Контрольований стан об'єкта – це такий стан, коли процес стабільний, а його середнє й розкид не змінюються. Вихід з контрольованого стану визначається за контрольною картою на підставі таких критеріїв:

·     вихід точок за контрольні межі;

·     серія – це прояв такого стану, коли точки незмінно виявляються по одну сторону від середньої лінії; число таких точок називається довжиною серії. Серія довжиною в сім точок розглядається як невипадкова. Навіть якщо довжина серії виявляється менше шести, у ряді випадків ситуацію варто розглядати як невипадкову, наприклад, коли:

а) не менш 10 з 11 точок виявляються по одну сторону від центральної лінії;

б)      не менш 12 з 14 точок виявляються по одну сторону від центральної лінії;

в) не менш 16 з 20 точок виявляються по одну сторону від центральної лінії.

·     тренд (дрейф). Якщо точки утворять криву, яка безупинно підвищується або знижується, кажуть, що має місце тренд.

·     наближення до контрольних зон (меж). Розглядаються точки, які наближаються до трисігмових контрольних меж, причому якщо 2 або 3 точки виявляються за двосігмовими лініями, то такий випадок треба розглядати як ненормальний.

·     наближення до центральної лінії. Коли більшість точок концентрується усередині центральних півторасігмових ліній, що обумовлено невідповідним способом розбиття на підгрупи. Наближення до центральної лінії зовсім не означає, що досягнуто контрольованого стану, навпаки, це значить, що в підгрупах змішуються дані з різних розподілів, що робить розмах контрольних меж занадто широким. У такому випадку треба змінити спосіб розбиття на підгрупи.

Одним з важливих етапів при складанні контрольних карт є спосіб визначення контрольних границь (границь регулювання). Для визначення контрольних границь необхідно зібрати велику кількість даних, що характеризують стан процесу, і на їх основі розрахувати контрольні нормативи. Зазвичай діапазон від середнього до границь регулювання містить трикратне середнє квадратичне відхилення. Розглянемо контрольні карти, які найбільш широко застосовуються у виробництві.

Контрольна карта індивідуальних значень (X)

Ця карта застосовується, якщо спостереження проводяться над невеликим числом об'єктів, і всі вони піддаються контролю. Спостереження ведуться над безперервним показником.

Порядок побудови контрольної карти (етапи побудови).

1.  Дані вимірювань аналізованої величини х послідовно реєструються в контрольному листку. Кожному значенню присвоюється номер i від 1 і далі. Коли набирається 25-30 значень х, етап спостережень закінчується.

2.  Обчислюються поточні розмахи R, як різниця між поточним і попереднім значеннями спостережуваної величини (без врахування знаку):

.

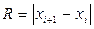3.  Усього виходить (n - 1) значень поточних розмахів.

4.  Обчислюється середнє значення аналізованої величини за період спостережень за формулою:

.

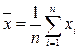5.  Обчислюється середнє значення розмаху за період спостережень за формулою:

.

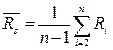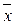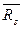6.  Отримані поточні значення xi і R наносяться на розташовані одне під одним графіки у відповідних масштабах. На ці графіки наносяться також середні значення  і  у вигляді середніх ліній.

7.  Обчислюються й наносяться на графіки нижня (LCL) і верхня (UCL) контрольні границі (границі регулювання) і середні лінії (CL):

,                ,                   ,

,               ,       .

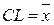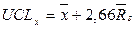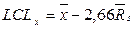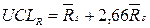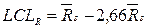8.  На цьому етап побудови контрольної карти завершується.

На етапі спостереження й регулювання процесу виконуються такі дії:

·     вимірюється значення спостережуваної величини й заноситься в контрольну карту;

·     обчислюється поточний розмах і його значення заноситься в контрольну карту.

Якщо отримані значення перебувають у межах контрольних границь, можна вважати, що процес є керованим, тобто стабільним. Якщо ж одна із точок виходить за межі контрольних границь, це є сигналом про неблагополуччя. Варто розібратися із причинами такого відхилення і за необхідності вжити потрібних заходів. Якщо точки не виходять за межі контрольних границь, але спостерігається серія точок, розташованих нижче або вище середньої лінії, це також є сигналом про розладнання процесу. Довжина такої «тривожної» серії - 6 точок. Але якщо серії, які спостерігаються, більш короткі, розділені окремими точками з іншої сторони від середньої лінії, це також є сигналом неблагополуччя.

 

Контрольна карта середніх значень і розмахів ()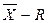

Карта типу 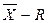 застосовується в масовому виробництві, коли карти типу X незастосовні через громіздкість. Під час використання карт типу  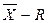висновки про стабільність (стійкість) процесу робляться на основі даних, отриманих під час аналізу невеликої кількості представників всіх розглянутих виробів. Для цього всі вироби поєднуються в партії в порядку виготовлення й від кожної партії беруться невеликі вибірки, за даними яких будується контрольна карта. Порядок її побудови такий:

1.  Визначається обсяг партій виробів, з яких беруться вибірки. Партія може складатися як виробіток за годину, зміну, або інший період часу, може формуватися з потоку однаковими групами виробів або іншим способом. Бажано, щоб партії були однаковими.

2.  З кожної партії відбирається певне число деталей – вибірка – звичайно від двох до десяти, залежно від завдань, необхідної точності, обсягу й способу контролю. Для кожної карти обсяг вибірки залишається постійним. Вибіркам присвоюються номери і від 1 до n. Усього береться 25 – 30 вибірок.

3.  У кожній вибірці – обчислюється середнє значення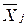 і розмах Rj:

,

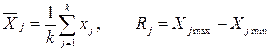де j – номер значення у вибірці;

k – обсяг вибірки.

4.  Після завершення періоду спостережень обчислюється загальне середнє значення спостережуваної величини 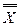 і середній розмах :

.

.

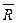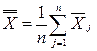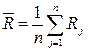Отримані значення наносяться на графік.

5. Обчислюються й наносяться на графік контрольні границі (границі регулювання) за формулами:

,              ,             ,

,              ,                             .

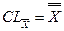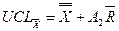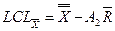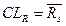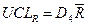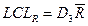Значення коефіцієнтів у цих формулах залежать від обсягу вибірки й наведені в таблиці 13.

 

Таблиця 13 – Коефіцієнти для визначення границь регулювання

Спостереження у вибірці n	Середні значення A2	Коефіцієнти для меж керованості
		D3	D4
2	1,88	-	3,267
3	1,023	-	2,574
4	0,729	-	2,282
5	0,577	-	2,114
6	0,483	-	2,004
7	0,419	0,076	1,924
8	0,373	0,136	1,864
9	0,337	0,184	1,816
10	0,308	0,223	1,777
11	0,285	0,256	1,744
12	0,266	0,283	1,717
13	0,249	0,307	1,693
14	0,235	0,328	1,672
15	0,223	0,347	1,653
16	0,212	0,363	1,637
17	0,203	0,378	1,622
18	0,194	0,391	1,608
19	0,187	0,403	1,597
20	0,18	0,415	1,585
21	0,173	0,425	1,575
22	0,167	0,434	1,566
23	0,162	0,443	1,557
24	0,157	0,451	1,548
25	0,153	0,459	1,541

 

Контрольна карта середніх значень і середніх квадратичних відхилень        ()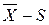

Дана карта практично ідентична карті (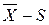), але точніша за неї та може рекомендуватися під час налагодження технологічних процесів в масовому виробництві відповідальних деталей. Її можна застосувати у випадках, коли є система вбудованого контролю з автоматичним введенням даних в ЕОМ, які використовуються для автоматичного керування процесом.

У картах 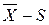 замість розмаху R використовується більш ефективна статистична характеристика розсіювання спостережуваних значень – середнє квадратичне відхилення (S). Вона показує, наскільки тісно групуються окремі значення навколо середнього арифметичного або як вони розсіюються навколо нього. Середнє квадратичне відхилення визначається за формулою:

.

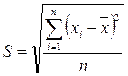В іншому побудова й застосування карти (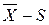) не відрізняється від карти ().

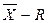Іноді для контролю використовується карта (Me – R) – контрольна карта медіан і розмахів. Медіана – це середнє значення у вибірці, якщо всі значення розташовані в порядку зростання або зменшення. У вибірці із трьох значень медіана – друге значення, у вибірці з п'яти значень медіана посідає третє місце. Така карта менш точна, ніж карта (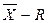), але вона простіша в користуванні й часто застосовується.

 

Порядок виконання і звітування

1. Ознайомитись з теоретичною частиною практичної роботи.
2. Виконати завдання 1, 2, 3 та 4 відповідно до варіанта виданого викладачем.

Варіанти завдань

Завдання 1. Діаграма Парето. Із загальної кількості деталей, виготовлених виробничою ділянкою в поточному місяці, 200 деталей мають дефекти. Після проведеної класифікації за групами дефектів одержали дані, подані в таблиці 14.

Дослідження причин появи бракованих деталей по кожній групі дало результати, подані в таблиці 15.

Відповідно до номера вашого варіанта, на основі наведених даних, поданих у таблицях 14 і 15 побудувати діаграму Парето по групах і причинах дефектів. Провести аналіз причин появи браку.

Завдання 2. Гістограма. Відповідно до номера вашого варіанта, на підставі даних, отриманих у результаті вимірювання коефіцієнта деформації одного з металевих матеріалів у процесі термообробки (таблиця 5) скласти гістограму (n – загальну кількість вимірювань; xi – результати i-го виміру).

Завдання 3. Контрольна карта. Побудувати контрольну карту розмахів і середніх арифметичних за результатами вимірювань довжини пластин в 25 вибірках, наведених у таблиці 17.

Таблиця 14 – Число дефектних деталей (шт.)

Варіант	Види дефектів
	Відхилення в розмірах	Раковини	Подряпини	Тріщини	Вигин	Інші
1	90	36	30	16	12	16
2	60	30	46	20	30	14
3	80	36	40	14	16	14
4	65	40	38	35	14	8
5	50	35	55	38	10	12
6	80	46	16	30	12	16
7	40	30	70	18	32	10
8	45	35	46	25	35	14
9	70	36	50	14	12	18
10	50	55	35	38	8	14
11	35	45	46	25	35	14
12	82	34	40	14	26	4
13	50	65	25	38	13	9
14	88	30	38	16	13	15
15	40	65	35	38	10	12
16	50	55	35	38	15	7
17	80	36	14	10	12	18
18	48	30	46	40	30	6

 

Таблиця 15 – Число дефектних деталей

Продовження таблиці 15

1	2	3	4	5	6	7
12	42	68	45	15	14	16
13	60	82	12	17	14	15
14	48	62	12	29	35	14
15	80	26	32	18	34	10
16	52	48	45	20	19	16
17	72	50	17	22	25	14
18	82	42	38	14	18	6

 

Таблиця 16 – Коефіцієнт деформації

Продовження таблиці 16

 

Продовження таблиці 16

 

Таблиця 17 – Розміри довжин металевих пластин

Номер вибірки	Номер виробу
	1	2	3	4	5
1	2	3	4	5	6
1	22,2	22,0	23,1	20,7	20,2
2	20,9	21,2	18,7	17,8	22,3
3	25,8	18,4	22,3	21,4	20,4
4	21,1	23,9	18,4	22,0	19,5
5	21,4	16,3	20,2	19,9	18,2
6	21,3	17,4	20,7	19,5	22,1
7	15,4	22,2	18,1	20,0	20,8
8	21,8	25,0	18,1	21,9	16,6
9	21,2	20,2	18,4	21,5	18,9
10	21,5	17,9	21,8	20,6	20,5
11	17,6	17,6	20,3	18,7	18,7
12	19,0	18,2	21,7	17,3	18,9
13	20,2	19,3	20,5	21,9	21,9
14	24,4	19,5	17,6	20,1	19,3
15	18,4	21,9	18,4	19,5	23,0

 

Продовження таблиці 17

1	2	3	4	5	6
16	23,6	20,2	20,3	20,3	19,2
17	24,3	17,1	20,7	21,4	16,0
18	14,6	16,3	20,6	19,0	20,8
19	22,1	20,1	22,4	20,9	20,2
20	23,5	21,4	19,4	20,9	19,4
21	21,4	21,0	22,5	22,9	23,1
22	20,2	20,0	20,3	22,4	23,4
23	19,4	18,8	21,7	14,3	22,6
24	19,0	19,3	20,8	19,7	21,7
25	21,2	21,4	18,5	20,4	19,9

 

Приклад виконання

 

Вихідні дані:

Види дефектів
Відхилення в розмірах		Раковини	Подряпини		Тріщини		Вигин	Інші
90		36	30		16		12	16
Причини дефектів
Спосіб установки	Недотримання режимів обробки		Стан оснащення	Форма заготовки		Стан устаткування		Інші
82	38		32	18		14		16

 

Аналіз Парето застосовується як для виявлення проблем або гострих питань, так і для аналізу причин, що викликають ці проблеми. Тому розрізняють два види діаграм Парето: за результатами діяльності та через причину.

Діаграма Парето за результатами діяльності призначена для виявлення основної проблеми, що викликає небажані результати діяльності.

Діаграма Парето через причину показує причини  проблем, що виникають  у виробництві, і використовується для виявлення головної з них.

Під час використання діаграми Парето найпоширенішим методом аналізу є так званий АВС-аналіз. Тут фактори, за якими проводиться аналіз, об’єднуються в три групи А, В, С:

•      на групу А припадає 70 - 80% всіх дефектів або витрат, якщо проводиться вартісний аналіз;

•      на групу С 5 - 10%;

•      проміжна група В характеризується 10 - 25% витрат, які пов’язані з помилками й дефектами в роботі.

Очевидно, що в першу чергу необхідно жорстко контролювати появу дефектів, які відносяться до групи А.

 

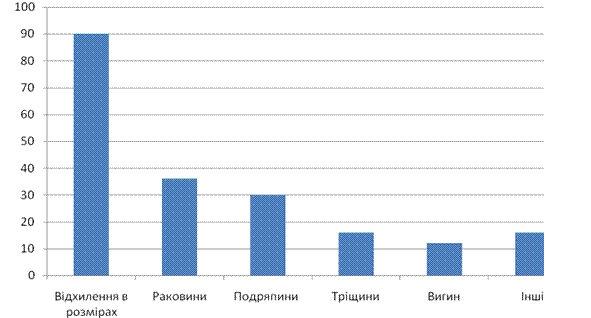
Рисунок 4 – Кількість дефектів по видах

 

З наведеної гістограми і графіка слідує, що основним дефектом під час виготовлення є відхилення розмірів готових виробів.

 

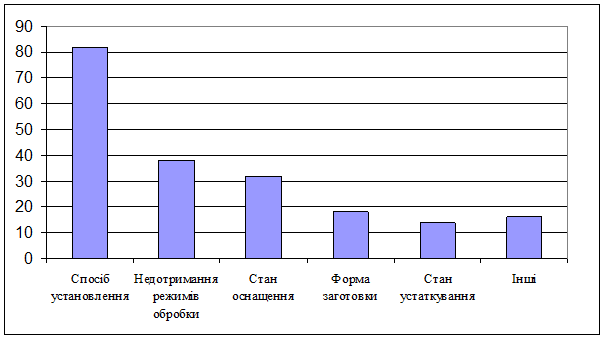
Рисунок 5 – Кількість дефектів спричинених певними чинниками

 

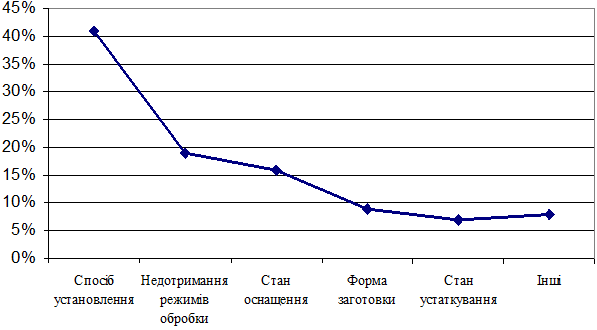
Рисунок 6 – Відсоток дефектів спричинених певними чинниками (браку)

 

Вважатимемо, що дефекти спричиняють втрати однакової тяжкості, тобто їх вага однакова. Тоді кількість дефектів кожного виду спричинена певним чинником розраховуватиметься за виразом

,

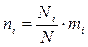де Ni – кількість дефектів спричинених і-им чинником;

N – загальна кількість дефектів;

mi – кількість дефектів певного виду.

Кількість дефектів кожного виду спричинена окремими чинниками подана в таблиці 18.

 

Таблиця 18 – Результат аналізу причин виникнення дефектів певних видів

	Відхилення в розмірах	Раковини	Подряпини	Тріщини	Вигин	Інші	Сума дефектів через причини
1	2	3	4	5	6	7	8
Спосіб установлення	36,9	14,76	12,3	6,56	4,92	6,56	82
Недотримання режимів обробки	17,1	6,84	5,7	3,04	2,28	3,04	38
Стан оснащення	14,4	5,76	4,8	2,56	1,92	2,56	32
Форма заготовки	8,1	3,24	2,7	1,44	1,08	1,44	18

 

 

Продовження таблиці 18

1	2	3	4	5	6	7	8
Стан устаткування	6,3	2,52	2,1	1,12	0,84	1,12	14
Інші	7,2	2,88	2,4	1,28	0,96	1,28	16
Сума дефектів по видам	90	36	30	16	12	16	200

 

З даних таблиці 18 випливає, що 76% браку спричиняє неправильна схема установлення деталей, недотримання режимів обробки та стан оснащення. З цього випливає, що для підвищення якості продукції, що випускатиметься, основну увагу слід звернути на ці фактори.

 

Задача 2

Основу будь-якого дослідження становлять дані, отримані в результаті контролю й вимірювання одного або декількох параметрів виробу (характеристики якості). У всіх галузях промисловості потрібне проведення аналізу точності й стабільності процесу, спостереження за якістю продукції, відстеження істотних показників виробництва. Шляхом вимірювання відповідних параметрів необхідними засобами одержують ряд даних, що являють собою неупорядковану послідовність значень параметра, на основі яких неможливо зробити коректні висновки. Тому для осмислення якісних характеристик виробів, процесів, виробництва (статистичних даних) часто будують гістограму розподілу.

Гістограма – це інструмент, що дозволяє наочно оцінити розподіл статистичних даних, згрупованих за частотою влучення даних у певний (заздалегідь заданий) інтервал.

Гістограма – це стовпцева діаграма, яка використовується для графічного подання наявної кількісної інформації, зібраної за тривалий період часу (тиждень, місяць, рік і т. д.), що подає важливу інформацію для оцінки проблеми й знаходження способів її вирішення. Гістограма застосовується головним чином для аналізу значень вимірюваних параметрів.

 

Вихідні дані: Коефіцієнт деформації

1,1 0,6 0,7 1,2 1,1

номер	Значення xi, n = 100
1	0,9	1,5	0,9	1,1	1,0	0,9	1,1	1,2	1,0	0,6	0,1	0,7	0,8	0,7	0,8	0,5	0,8	1,2	0,6
	0,5	0,8	0,3	0,4	0,5	1,0	1,1	1,2	0,4	0,6	0,7	0,5	0,2	0,5	0,3	0,5	0,4	1,0	0,8
	0,7	0,8	0,3	0,4	0,6	0,7	1,1	1,2	0,8	0,8	1,1	0,6	1,0	0,7	0,6	0,3	1,2	1,4	1,0
	1,0	0,9	1,0	1,2	1,3	0,9	1,3	1,4	1,0	1,4	1,4	0,9	1,1	0,9	1,4	0,9	1,8	0,9	1,4
	1,1	1,4	1,4	1,4	0,9	1,1	1,4	1,3	1,1	1,5	1,6	1,6	1,5	1,6	1,5	1,6	1,7	1,8	1,5

 

 

Таблиця 19 – Розрахунок параметрів вибірки за допомогою Microsoft Excel

Сума всіх значень таблиці	97,2
Кількість значень в таблиці	100
Середнє значення параметра	0,972
Найбільше значення	1,8
Найменше значення	0,1
Розмах функції	1,7
Розрахункова кількість інтервалів	15,83785834
Прийнята кількість інтервалів	16
Ширина інтервалу	0,10625

 

Таблиця 20 – Визначення характеристик розподілу коефіцієнта деформації

Границі інтервалів		Частість	Частоста	Накопичена частота
нижня межа	верхня межа
0,1	0,20625	2	0,02	0,02
0,20625	0,3125	4	0,04	0,06
0,3125	0,41875	4	0,04	0,1
0,41875	0,525	6	0,06	0,16
0,525	0,63125	7	0,07	0,23
0,63125	0,7375	7	0,07	0,3
0,7375	0,84375	8	0,08	0,38
0,84375	0,95	10	0,1	0,48
0,95	1,05625	9	0,09	0,57
1,05625	1,1625	11	0,11	0,68
1,1625	1,26875	7	0,07	0,75
1,26875	1,375	3	0,03	0,78
1,375	1,48125	10	0,1	0,88
1,48125	1,5875	5	0,05	0,93
1,5875	1,69375	4	0,04	0,97
1,69375	1,8	3	0,03	1
Сума всіх значень ствопця		100	1

 

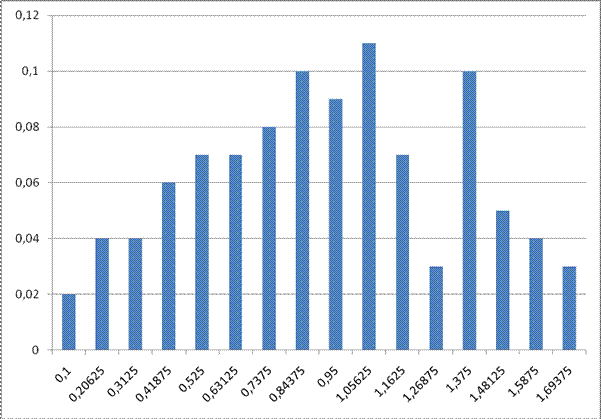
Рисунок 7 - Відносна частота появи коефіцієнтів деформації в певному діапазоні

 

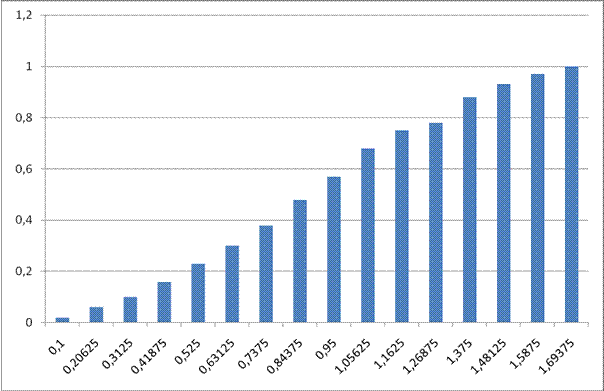
Рисунок 8 - Накопичена частота появи коефіцієнтів деформації в певному діапазоні

Завдання 3

Контрольна карта. Побудувати контрольну карту розмахів і середніх арифметичних за результатами вимірів довжини пластин в 25 вибірках, наведених у таблиці 17.

 

Таблиця 21 – Розрахунок розмахів і середніх арифметичних довжин пластин

Номер вибірки	Номер виробу					Сума вибірки	Середнє значення вибірки	Розмах вибірки
	1	2	3	4	5
1	22,2	22	23,1	20,7	20,2	108,2	21,64	2,9
2	20,9	21,2	18,7	17,8	22,3	100,9	20,18	4,5
3	25,8	18,4	22,3	21,4	20,4	108,3	21,66	7,4
4	21,1	23,9	18,4	22	19,5	104,9	20,98	5,5
5	21,4	16,3	20,2	19,9	18,2	96	19,2	5,1
6	21,3	17,4	20,7	19,5	22,1	101	20,2	4,7
7	15,4	22,2	18,1	20	20,8	96,5	19,3	6,8
8	21,8	25	18,1	21,9	16,6	103,4	20,68	8,4
9	21,2	20,2	18,4	21,5	18,9	100,2	20,04	3,1
10	21,5	17,9	21,8	20,6	20,5	102,3	20,46	3,9
11	17,6	17,6	20,3	18,7	18,7	92,9	18,58	2,7
12	19	18,2	21,7	17,3	18,9	95,1	19,02	4,4
13	20,2	19,3	20,5	21,9	21,9	103,8	20,76	2,6
14	24,4	19,5	17,6	20,1	19,3	100,9	20,18	6,8
15	18,4	21,9	18,4	19,5	23	101,2	20,24	4,6
16	23,6	20,2	20,3	20,3	19,2	103,6	20,72	4,4
17	24,3	17,1	20,7	21,4	16	99,5	19,9	8,3
18	14,6	16,3	20,6	19	20,8	91,3	18,26	6,2
19	22,1	20,1	22,4	20,9	20,2	105,7	21,14	2,3
20	23,5	21,4	19,4	20,9	19,4	104,6	20,92	4,1
21	21,4	21	22,5	22,9	23,1	110,9	22,18	2,1
22	20,2	20	20,3	22,4	23,4	106,3	21,26	3,4
23	19,4	18,8	21,7	14,3	22,6	96,8	19,36	8,3
24	19	19,3	20,8	19,7	21,7	100,5	20,1	2,7
25	21,2	21,4	18,5	20,4	19,9	101,4	20,28	2,9

 

Загальне середнє значення вибірки	20,2896
Загальний середній розмах вибірки	4,724

Згідно з довідниковими даними вибираємо коефіцієнти для визначення границь регулювання і побудови контрольної карти:                А2 = 0,577; D3 = 0,076; D4 = 2,114.

 

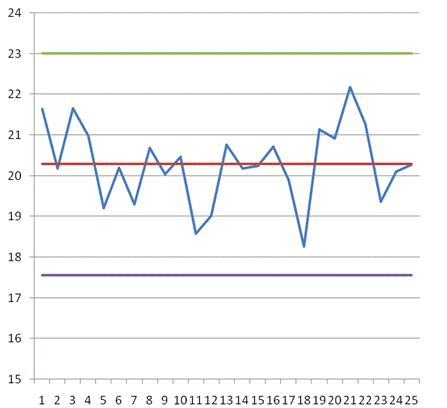
Рисунок 9 – Контрольна карта середніх арифметичних

 

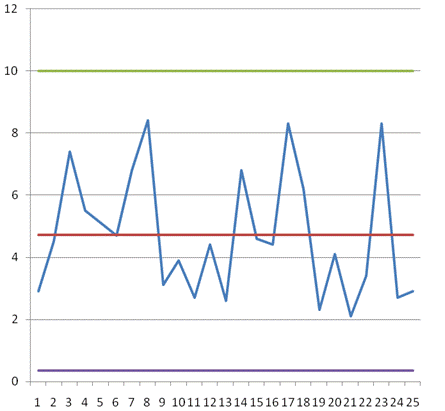
Рисунок 10 – Контрольна карта розмахів

Контрольні запитання

1.     Для чого застосовується аналіз Парето?

2.     В чому полягає суть АВС-аналізу?

1. Гістограма. Принцип побудови.
2. Основні типи розподілів даних на гістограмах.
3. Висновки, які можна зробити по гістограмам розподілу даних.
4. Типи контрольних карт Шухарта.
5. В яких випадках і які контрольні карти Шухарта застосовуються?

---