1 МОДЕЛЮВАННЯ. ОСНОВНІ ПОНЯТТЯ

Сучасне виробництво, в тому числі і автомобільного транспорту (road transport), потребує широкого застосування методів моделювання і особливо оптимізаційного.

Для автомобільного транспорту (АТ) розрахункові методи моделювання дозволяють визначити необхідне число постів обслуговування, запасних частин та інших ресурсів для здійснення транспортного процесу.

Основним виробничим процесом АТ є транспортний. На здійснення цього процесу працює ряд служб АТП – технічна, комерційна (експлуатації), служба постачання, служба головного механіка і т. д.

Кожна служба веде своє виробництво (Вир), яке визначає свої конкретні цілі (Ц), для досягнення яких потрібно рішення певних завдань (З), кожна з яких вимагає свої методи вирішення (Р).

Всю цю послідовність дій можна представити у вигляді виразу:

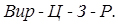(1.1)

У навчальному посібнику розглядаються всі складові цього виразу.

При вивченні технологічного процесу, останній замінюють моделлю з метою економії витрат (грошових, тимчасових, трудових).

Модель (model) – це аналог, макет чи інший вид відображення найбільш істотних властивостей досліджуваного процесу або явища.

1.1 Моделі. Математичні моделі

Математичними моделями (mathematical model) називають комплекс математичних залежностей і логічних виразів, що відображають суттєві характеристики досліджуваного явища (процесу). Математичні залежності встановлюють залежність між відомими і шуканими величинами.

Модель – це відображення системи, що досліджується, або деяких явищ, що нас цікавлять (процесів, подій). Моделі використовуються в цілях управління і прогнозування (передбачення) можливої ефективності системи в разі зміни її характеристик. Вони дозволяють пояснити явища, що нас цікавлять, і виявити взаємозв'язок окремих явищ, а також замінити дорогі і складні випробування систем в реальній обстановці. Моделювання здійснюється з метою удосконалення системи, а також для ознайомлення і навчання персоналу з системами і ситуаціями, які важко здійснити в реальних умовах. За допомогою моделі можна перевіряти або демонструвати нові ідеї, отримувати кількісну оцінку при різних варіантах управління. Діяльність, наприклад, автотранспортного підприємства можна розглядати в уповільненому або прискореному темпі. При моделюванні можна заглянути вперед і розглянути «майбутній» стан системи.

Моделі можна розділити на три типи: образотворчі (портретні), аналогові й символічні (логіко-математичні). Образотворчі (портретні) моделі або моделі геометричної подібності точно копіюють оригінал і відображають зовнішні характеристики системи – фотографії, макети виробничих корпусів, ситуаційні плани, моделі автомобілів або двигунів і т. д. За допомогою цих моделей можна описати явище (об'єкт), але не можна пояснити або встановити причинні зв'язки і передбачити можливі зміни.

Аналогові моделі (analogue model) служать для опису перебігу перехідних процесів в різних механічних і електричних системах і пов'язують властивості оригіналу з іншими більш наочними властивостями. Ці моделі дозволяють, наприклад, уявити дорожню мережу лініями різного кольору або рельєф місцевості за допомогою горизонталей. Температура повітря, наприклад, представляється графічно по висоті рівня в термометрі і т. д.

У складніших логіко-математичних (символічних) моделях (symbolic model) використовуються символи математичного або логічного характеру для відображення властивостей системи і пояснення явищ. Розрізняють два методи вирішення і аналізу цих моделей: аналітичний (дедуктивний) і чисельний (індуктивний). Аналітичні моделі базуються на аналітичних формульних залежностях між параметрами задачі (алгебраїчні, диференційні та інші рівняння). На практиці зустрічаються такі види моделей: фізичні, математичні, графічні, аналогові, механічні та ін.

Існують і інші моделі: моделі транспортних процесів в задачах лінійного програмування; теорії масового обслуговування; мережевих графіків.

Зазвичай при вирішенні практичних завдань, заснованих на дослідженні операцій, доводиться розглядати кілька послідовних і взаємопов'язаних частин (стадій). До них відносяться постановка (формулювання) задачі; складання математичної моделі керованої системи; складання плану, проведення контрольних експериментів і відшукання рішення за допомогою цієї моделі; перевірка даної моделі і прийняття рішення, уточнення рішення і застосування його на практиці.

Прикладами математичних моделей можуть служити такі залежності:

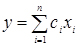- лінійна залежність,

де ci - параметр; xi - змінні; y - шукана величина.

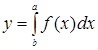- інтеграл для обчислення площі, роботи, швидкості і т.д.

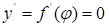- математична модель пошуку екстремуму функції f(x) .

Переваги математичних моделей (математичного моделювання) перед іншими полягають:

а) у низькій вартості їх створення;

б) у швидкому отриманні результатів дослідження;

в) у можливості проведення розрахункових експериментів і перевірки правильності побудови моделі.

До недоліків математичних моделей слід віднести те, що вони абстрактні. Математичні моделі можна класифікувати по ряду ознак. Одна з класифікацій за характером параметра, змінної і увазі залежності наведена на рис. 1.1. Детермінованими називають такі моделі, в яких значення параметра і змінних величин передбачаються заданими і достовірними при жорстких зв'язках. Стохастичні моделі – описують випадкові процеси, тобто процеси, що протікають під дією випадкових факторів (задачі теорії ймовірності – імовірнісні закони, теорія масового обслуговування).

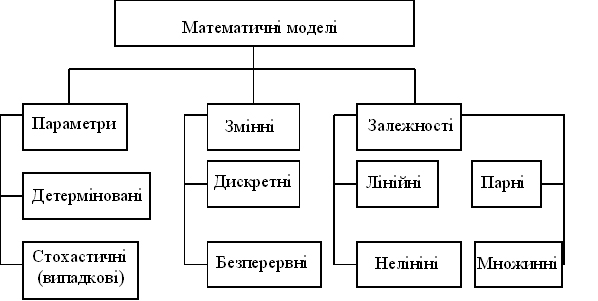
Рисунок 1.1 – Класифікація математичних моделей

1.2 Оптимізаційне моделювання

Сучасне виробництво вимагає широкого використання методів оптимізації (optimization method). Розмірність виробничих оптимізаційних завдань, як правило, велика, тому вирішувати їх доцільно на ЕОМ. Одна і та ж задача може бути вирішена різними методами одночасно, в той час, коли різні задачі можуть вирішуватися одним методом. У будь-якому випадку повинні послужити оптимальні (як вигідно) показники виробничого процесу.

Всі методи оптимізації умовно можна розділити на класичні та сучасні.

До класичних методів відносять: методи диференційного числення; чисельні методи; методи умовної і безумовної оптимізації; методи перебору варіантів.

До сучасних методів можна віднести: лінійне програмування; нелінійне програмування; динамічне програмування; стохастичне програмування; теорія масового обслуговування; мережеве планування; теорія ігор, теорія планування експерименту.

1.3 Критерії оптимізації

При вирішенні оптимізаційних завдань спочатку треба встановити математичну модель (математичну залежність) виду досліджуваного процесу. При цьому вона повинна адекватно відображати його властивості. Надалі математичну залежність виду , яку необхідно дослідити на оптимальність, будемо називати цільовою функцією. Якщо в показник цільової функції W вкладений фізичний зміст, то його разом з цільовою функцією називають критерієм оптимізації (критерій ефективності). Одним з найважливіших питань оптимізаційного моделювання виробничих процесів є вибір критерію оптимізації та опис його цільової функції. Розрізняють часткові і загальні критерії оптимізації. Загальні критерії, як правило, характеризують народногосподарський ефект підприємства (прибуток, собівартість, рентабельність і т.д.). Часткові критерії – окремі сторони виробничого процесу (витрати праці, зарплата і т.д.).

1.4 Основні етапи оптимізаційного моделювання

Основними етапами оптимізаційного моделювання є наступні:

1. Постановка завдання. Вона включає в себе обстеження об'єкта (процесу), вивчення факторів, що впливають на досліджуваний об'єкт, виявлення істотних факторів, формулювання завдання.

2. Побудова математичної моделі. У загальному вигляді вона записується max (min)  при обмеженнях (на ресурси і т.д.):

Графічно математичну модель процесу можна представити так (рис. 1.2).

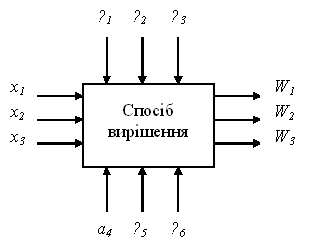
α1, α2, α3– зовнішні некеровані фактори; α4, α5, α6 – внутрішні некеровані фактори; W1, W2, W3 – критерії ефективності (цільова функція);

x1, x2, x3 – керовані змінні

Рисунок 1.2 – Графічна модель процесу

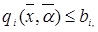
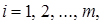(1.2)

де W – цільова функція (показник ефективності);

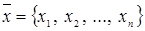– вектор керованих змінних;

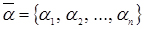–  вектор некерованих змінних;

qi, bi – функція обмеження та показник обмеження.

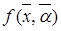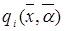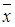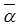3. Знаходження методу вирішення. Залежно від структури цільової функції і обмежень застосовується той чи інший метод розв'язку: а) якщо  і  - лінійні функції щодо змінних  і , то маємо лінійне програмування; б) якщо  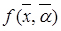і 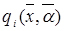 - нелінійні функції, то маємо нелінійне програмування; в) якщо 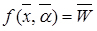можна представити у вигляді суми 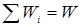, і завдання розбивається на ряд "кроків" (етапів), то застосовують динамічне програмування; г) якщо  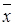і 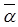 випадкові величини, то застосовується стохастичне програмування (моделювання).

4. Перевірка і корегування моделі. Тут перевіряється відповідність математичної моделі реальному процесу.

5. Вирішення задачі та її реалізація на практиці. Розмірність виробничих завдань автомобільного транспорту, як правило, велика, тому вирішувати їх доцільно на ЕОМ. Якщо в якості обробки даних виступає ЕОМ, то рішення задачі можна розбити на наступні окремі етапи (рис. 1.3).

Перший етап (постановка завдання) полягає у вивченні досліджуваного явища, формулюванні завдання і цілей її вирішення.

Визначаються вихідні дані та очікувані результати (їх зміст, обсяг, достовірність описуваного явища).

Цей етап закінчується словесним описом завдання. Перший етап безпосередньо пов'язаний з другим «Математичне формулювання завдання». У підсумку другого етапу має бути отримана математична модель.

На третьому етапі "Розробка методу вирішення" проводиться вибір доцільного (оптимального) математичного методу вирішення поставленого завдання. Результат – математичний опис обраного методу розв'язання.

Четвертий етап - "Складання алгоритму вирішення" завдання. Тут виробляється детальний аналіз обраного методу розв'язання. Складається з необхідним ступенем деталізації за допомогою блок – схеми.

Етап "Програмування" (programming) полягає в запису розробленого алгоритму на одній з мов програмування. Етапи 5, 6, 7 відповідають етапу налагодження програми на ЕОМ.

Після отримання правильних результатів за всіма контрольними прикладами програма вважається налагодженою і готовою до експлуатації.

Етап "вирішення задачі" полягає в отриманні результатів для різних варіантів вихідних даних. Цей етап є розрахунком за програмою.

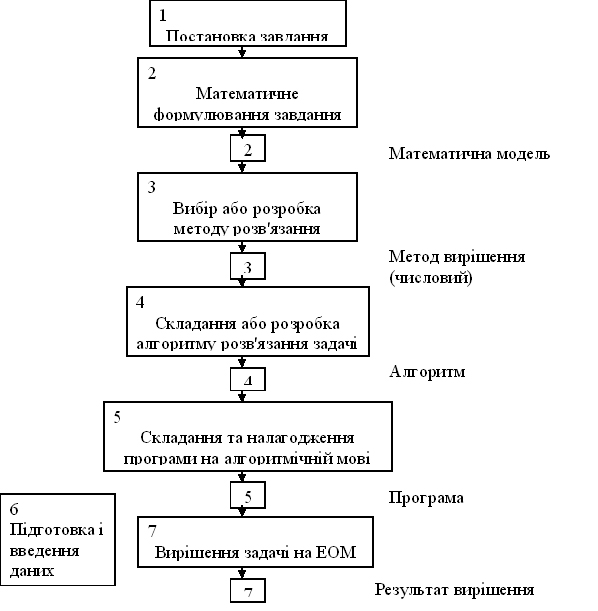
Рисунок 1.3 – Послідовність підготовки і рішення задач на ЕОМ

Контрольні запитання

1. Перерахуйте служби АТП, які забезпечують транспортний процес підприємства. Дайте визначення поняттям: модель, математична модель.

2. Класифікація математичних моделей, їх особливості.

3. Які переваги математичної моделі. Поняття алгоритм, програма

4. Перерахуйте сучасні методи оптимізації.

5. Перерахуйте класичні методи оптимізації.

6. Дайте визначення поняттям: цільова функція, критерій оптимізації.

7. Види критеріїв оптимізації

8. Перерахуйте основні етапи оптимізаційного моделювання.

9. Послідовніст підготовки і вирішення задач на ЕОМ.