2 МАТЕМАТИЧНІ ФУНКЦІЇ. МОДЕЛІ НА ЇХ ОСНОВІ
2.1 Основи регресійного аналізу
При обробці експериментальних даних і побудові математичних моделей використовують теорію кореляційно-регресійного аналізу (theory of correlation and regression analysis).
Регресійний аналіз (regression analysis) встановлює математичну модель, що зв'язує залежну змінну у с досліджуваної змінної х, тобто дозволяє отримати залежність виду 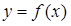 - рівняння парної регресії.
- рівняння парної регресії.
Значення змінної у може залежати відразу від декількох змінних 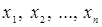 . У результаті обробки таких статистичних даних можна отримати залежність виду
. У результаті обробки таких статистичних даних можна отримати залежність виду 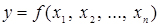 - рівняння множинної регресії. Всі рівняння регресії поділяються на лінійні і нелінійні.
- рівняння множинної регресії. Всі рівняння регресії поділяються на лінійні і нелінійні.
Функцію, апроксимуючу досвідчені дані, називають теоретичною функцією. При парній залежності експериментальні дані можуть бути апроксимовані за допомогою наступних функцій:
- прямою лінією 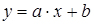 ;
;
- параболою другого порядку 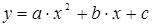 ;
;
- гіперболою 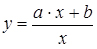 ;
;
- логарифмічною функцією 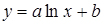 ;
;
- степеневою функцією 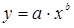 ;
;
- показовою функцією 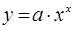 ;
;
- арифметичною прогресією 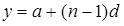 ;
;
- геометричною прогресією 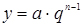 ;
;
- алгебраїчним поліномом, тобто рядом Маклорена:
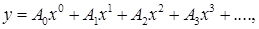 (2.1)
(2.1)
в якому коефіцієнти ряду визначаються за формулами:
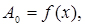
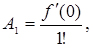
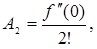 і т.д.;(2.2)
і т.д.;(2.2)
- тригонометричним рядом, тобто рядом Фур'є
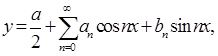 (2.3)
(2.3)
та іншими функціями.
Для двухфакторної регресійної залежності досвідчені дані можуть апроксимували наступними функціями:
- площиною 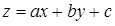 ;
;
- параболоїдом другого порядку 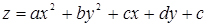 ;
;
- гіперболоїдом 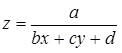 і т.д.
і т.д.
У загальному випадку для п-мірного простору і п змінних рівняння регресії другого порядку виглядає так:
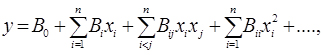 (2.4)
(2.4)
де у - досліджувана ознака (параметр) як функція багатьох змінних;
xi - фактори, що роблять вплив на параметр;
Bi- приватні коефіцієнти регресії, що показують вплив фактора xi на досліджувану ознаку;
Bij- коефіцієнти, що характеризують подвійний (парний) вплив факторів xi і xj на досліджувану ознаку.
2.2 Функціональні та кореляційні залежності
Розрізняють функціональні (functional) і кореляційні (correlation) залежності. Під функціональною розуміють таку залежність, коли зі зміною одного фактора змінюється інший, при цьому одному значенню незалежного фактора відповідає тільки одне значення залежного фактора (рис. 2.1).
Кореляційна залежність - це така залежність, при якій зміна однієї випадкової величини викликає зміну середнього значення іншої, тобто одному значенню незалежної змінної можуть відповідати кілька значень залежної змінної (рис. 2.2.). Тому кореляційні залежності можуть бути встановлені тільки при обробці великої кількості спостережень.
При обробці таких залежностей користуються кореляційним аналізом, який встановлює кількісну оцінку тісноти зв'язку між досліджуваними ознаками (факторами (factors)). Тісноту зв'язку (наявність кореляції) між двома величинами можна визначити візуально по полю кореляції.
Кореляційним полем називають нанесені на графік (див. рис. 2.2.) в певному масштабі точки, відповідні одночасно значенням двох величин. У нашому випадку тіснота зв'язку між параметрами х і у визначається візуально по співвідношенню короткою і поздовжньою осей еліпса розсіювання спостережень, нанесених на поле кореляції. Чим більше відношення поздовжньої осі до короткої, тим зв'язок тісніший.
Більш точно тіснота зв'язку оцінюється коефіцієнтом кореляції r . Коефіцієнт кореляції лежить в межах 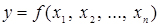 . При r=0 зв'язку немає.
. При r=0 зв'язку немає.
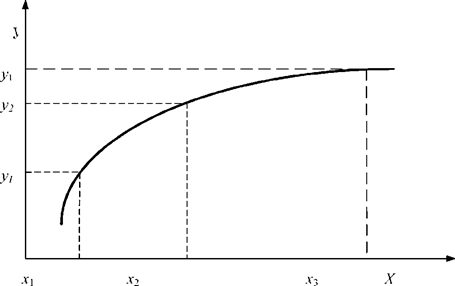
Рисунок 2.1 – Графік функціональної залежності
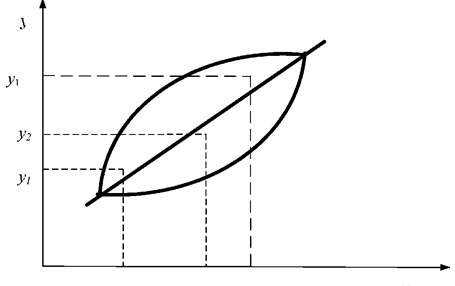
Рисунок 2.2 – Графік кореляційної залежності
Якщо  , то між двома величинами існує функціональний зв'язок.
, то між двома величинами існує функціональний зв'язок.
Отже, за величиною коефіцієнта кореляції можемо зробити наступний висновок:
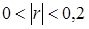 - зв'язку практично немає;
- зв'язку практично немає;
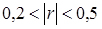 - зв'язок слабкий;
- зв'язок слабкий;
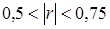 - зв'язок середній;
- зв'язок середній;
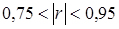 - зв'язок сильний;
- зв'язок сильний;
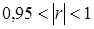 - практично функціональний зв'язок.
- практично функціональний зв'язок.
При позитивних спостерігається прямий зв'язок, тобто із збільшенням незалежної змінної збільшується і залежна. при негативному коефіцієнті кореляції існує зворотний зв'язок - зі збільшенням незалежної змінної залежна змінна зменшується. Існує ряд формул для розрахунку коефіцієнта кореляції (correlation coefficient).
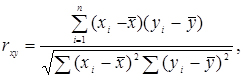 (2.5)
(2.5)
де rxy - коефіцієнт кореляції; xi , yi - поточні значення спостережуваних величин; 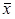 ,
, 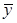 - середні значення цих величин.
- середні значення цих величин.
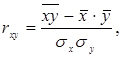 (2.6)
(2.6)
де 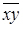 - середнє значення добутку двох кореляційних величин;
- середнє значення добутку двох кореляційних величин; 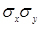 - середні квадратичні відхилення відповідних величин, які визначаються так:
- середні квадратичні відхилення відповідних величин, які визначаються так:
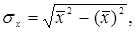
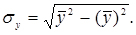 (2.7)
(2.7)
Для лінійної регресії коефіцієнт кореляції r є не тільки критерієм тісноти зв'язку, але і критерієм точності апроксимації (підбору формули, що виражає залежність).
Оцінка точності апроксимації (accuracy approximation) криволінійної залежністю проводиться за допомогою кореляційного відношення:
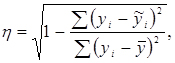 (2.8)
(2.8)
де yi - поточні значення залежної змінної; 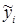 - теоретичні значення;
- теоретичні значення;
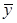 - середні значення.
- середні значення.
Кореляційне відношення приймає значення 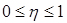 , воно завжди позитивно. Якщо
, воно завжди позитивно. Якщо 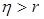 , то крива точніше апроксимує залежність, ніж пряма; для прямої
, то крива точніше апроксимує залежність, ніж пряма; для прямої 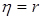 . Додатковою оцінкою точності апроксимації часто застосовують при оцінці нелінійної регресії, являється середня відносна помилка апроксимації
. Додатковою оцінкою точності апроксимації часто застосовують при оцінці нелінійної регресії, являється середня відносна помилка апроксимації 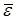 , яка визначається за формулою
, яка визначається за формулою
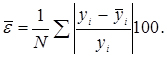 (2.9)
(2.9)
При оцінці взаємного впливу трьох і більше змінних використовують коефіцієнт множинної кореляції R, який для трьох змінних визначається за формулою:
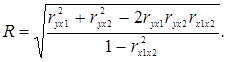 (2.10)
(2.10)
При розрахунку сукупного коефіцієнта кореляції необхідно попередньо визначити парні коефіцієнти кореляції ryx1, ryx2, ryx3. Після того як всі вони визначені, їх записують в квадратну симетричну матрицю
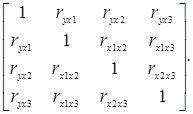 (2.11)
(2.11)
Тоді множинний коефіцієнт кореляції визначається формулою
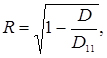 (2.12)
(2.12)
де D - визначник матриці парних коефіцієнтів кореляції; D11 - визначник тієї ж матриці з викресленими першим рядком і першим стовпцем, тобто визначник матриці парних коефіцієнтів кореляції між чинниками незалежними змінними.
2.3 Метод найменших квадратів
У практичній роботі залежність між змінними величинами часто виходить в результаті досліду (вимірювань). Зазвичай в цьому випадку залежність виявляється заданої у вигляді таблиці.
Функції, задані таким чином, можуть входити в подальші операції та розрахунки. Для зручності користування такими залежностями необхідно спочатку підібрати формулу, яка добре описує досвідчені дані. Підбір такої формули є суттєвою частиною обробки експериментальних даних. Одним з методів отримання цих формул є спосіб найменших квадратів.
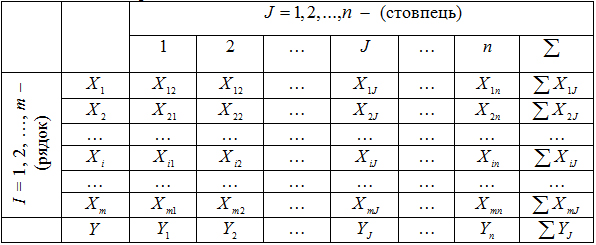
Нехай в результаті дослідів знайдені деякі значення xi , і відповідні їм значення yi які задані табл. 2.1.
Таблиця 2.1 – Значення xi і відповідні їм значення yi
x |
x1 |
… |
xi |
… |
xn |
y |
y1 |
… |
yi |
… |
yn |
Потрібно знайти залежність y=f(x) . Такою залежністю може бути одна з наступних:
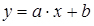 - лінійна;
- лінійна;
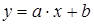 - степенева;
- степенева;
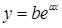 - показникова;
- показникова;
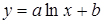 - логарифмічна;
- логарифмічна;
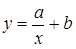 - гіперболічна і т. д.
- гіперболічна і т. д.
Метод найменших квадратів (method of least squares) дозволяє підібрати більш точні значення параметрів а і b. Попередньо необхідно встановити загальний вигляд аналітичної функції, який можна виявити за дослідними даними, якщо їх нанести на площину з координатами хОу.
Залежність У від X, зображується аналітичною функцією , не може збігатися з експериментальними значеннями у всіх п точках. Це означає, що для всіх або деяких точок маємо різницю (рис. 2.3.) відмінну від нуля
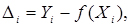 (2.13)
(2.13)
Метод найменших квадратів полягає в тому, що підбираються параметри а і b таким чином, щоб сума квадратів різниць (2.1) (рис. 2.3.) була найменшою, тобто
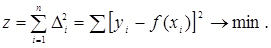 (2.14)
(2.14)
Нехай вид функції 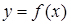 встановлено, то її можна представити у вигляді
встановлено, то її можна представити у вигляді
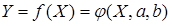 (2.15)
(2.15)
де а і b - шукані параметри.
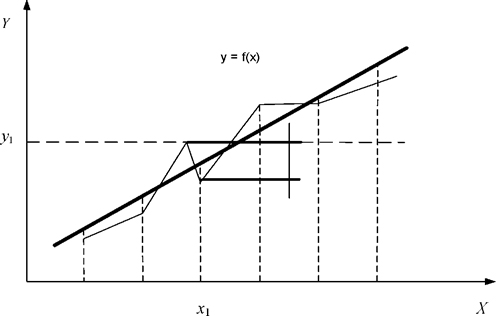
Рисунок 2.3 – Теоретична і експериментальна залежності
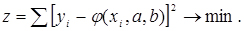 (2.16)
(2.16)
Для знаходження мінімуму виразу (2.13) обчислимо приватні похідні по аргументам а і b видання і прирівняємо ці похідні до нуля, отримаємо:
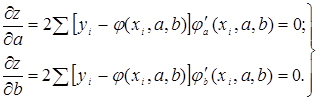 (2.17)
(2.17)
Система (2.17) містить два рівняння з двома невідомими. Вирішивши систему, знайдемо значення параметрів а і b. При знайдених значеннях параметрів величина Z буде найменшою, тобто, аналітична залежність буде найкращим чином описувати експериментальні дані.
Приклад: емпіричні дані необхідно описати лінійною залежністю:
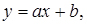 тобто
тобто 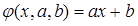 . (2.18)
. (2.18)
Тоді, згідно з методом найменших квадратів, запишемо:
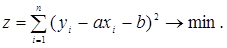 (2.19)
(2.19)
Вибираємо числа а і b так, щоб величина z була найменшою, для чого знайдемо приватні похідні виразу (2.15) по а і b, отримаємо:
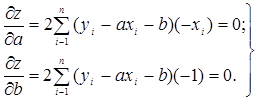 (2.20)
(2.20)
Ці дві умови дають нам таку систему рівнянь:
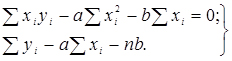 (2.21)
(2.21)
З системи (2.21) одержуємо:
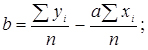 ;
;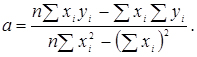 (2.22)
(2.22)
При вирішенні рівнянь (2.22), доцільно представити проміжні розрахунки у вигляді табл. 2.2.
Таблиця 2.2 – Проміжні розрахунки
і |
Xi |
Yi |
XiYi |
X2i |
1 |
X1 |
Y1 |
X1Y1 |
X21 |
2 |
X2 |
Y2 |
X2Y2 |
X22 |
… |
|
|
|
|
n |
Xn |
Yn |
XnYm |
X2n |
Разом |
Xi |
Yi |
XiYi |
X2i |
Примітка. Якщо нас цікавить нелінійна залежність, то проводячи аналогічний розрахунок для обраного типу функції, отримаємо відповідні вирази параметрів а і b. Однак цього можна і не робити, якщо є можливість перейти від нелінійної залежності до лінійної:
а) нехай 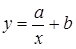 ; замінимо
; замінимо 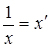 , отримаємо лінійну залежність
, отримаємо лінійну залежність
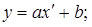
б)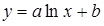 ; замінимо
; замінимо 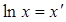 , отримаємо
, отримаємо
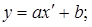
в)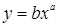 ; логарифмуючи, отримаємо
; логарифмуючи, отримаємо 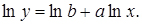
Замінимо 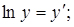 ;
; 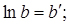 ;
; 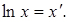
Маємо 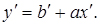
г) 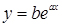 ; логарифмуючи, отримаємо
; логарифмуючи, отримаємо 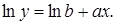
Вважаючи, що 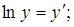 ;
; 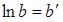 , маємо
, маємо 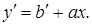
Для лінійних залежностей коефіцієнти 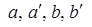 знаходимо з (2.22).
знаходимо з (2.22).
Зведення нелінійної регресії до лінійної виконується за допомогою лінеарізующих перетворень в ході введення 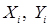 і при виведенні а і b.
і при виведенні а і b.
2.4 Множинна регресія
Ряд завдань автомобільного транспорту вимагають побудови множинних регресій (multiple regression) виду:
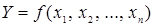 (2.23)
(2.23)
Так, якщо будемо розглядати діяльність АТП, то одним з основних показників його роботи є коефіцієнт випуску автомобілів на лінію - , на формування якого впливає велика кількість факторів.
Основними з них будуть:
X1 - забезпеченість водіями;
X2 - забезпеченість ремонтними робітниками;
X3 - забезпеченість інженерними кадрами;
X4 - забезпеченість запасними частинами і т.д.
Для розглянутого випадку:
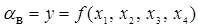 ,(2.24)
,(2.24)
тобто маємо справу з побудовою множинної регресії.
У більш загальному вигляді лінійна множинна регресія записується так:
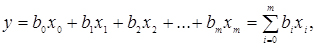 (2.25)
(2.25)
де у - теоретичне значення результативної ознаки;
xi - аргументи (фактори);
m - число досліджуваних факторів;
bi - коефіцієнти регресії, що показують ступінь впливу кожного з факторів на функцію;
b0 - залишковий член, що характеризує середнє значення функції.
Для отримання таких регресій необхідно скористатися статистичними (експериментальними) даними, які в загальному випадку можна представити таблицею 2.3. Процес побудови множинної регресії пояснимо на прикладі.
Приклад. Для випадку y=f(x1,x2) лінійна регресія має вигляд y=a+bx1+cx2 . При обчисленні коефіцієнтів a,b,c скористаємося методом найменших квадратів. Тоді будемо мати:
Таблиця 2.3 – Регресія зі статистичними даними
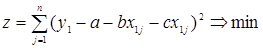 (2.26)
(2.26)
Розрахуємо приватні похідні виразу 2.26 за параметрами :
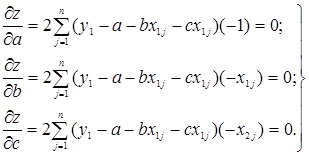 (2.27)
(2.27)
Перетворюючи систему (2.27), отримаємо
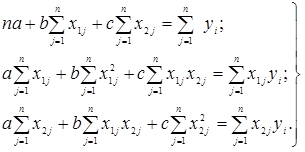 (2.28)
(2.28)
Система (2.28) представляє систему лінійних рівнянь, вирішуючи яку одним з відомих методів, знайдемо значення невідомих параметрів a,b,c.
Методом Крамера параметри a,b,c визначаються з виразів:
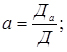 ;
;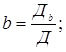 ;
;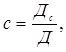
де Д - головний визначник системи лінійних рівнянь (2.28);
Да - визначник системи рівнянь, в якому стовпець коефіцієнтів при а замінений стовпцем вільних членів;
Дb - визначник системи, в якій стовпець коефіцієнтів при b замінений стовпцем вільних членів;
Дc - визначник системи, в яких стовпець коефіцієнтів при c замінений стовпцем вільних членів.
Якщо потрібно побудувати математичну модель виду 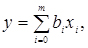 то для обчислення коефіцієнтів
то для обчислення коефіцієнтів 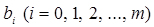 знову скористаємося методом найменших квадратів, отримуємо систему нормальних рівнянь виду
знову скористаємося методом найменших квадратів, отримуємо систему нормальних рівнянь виду
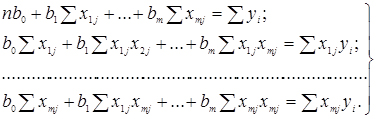 (2.29)
(2.29)
Вирішуючи систему (2.26) відомим методом, знайдемо значення параметрів bi рівняння регресії. Найбільш поширеним методом вирішення системи (2.26) є метод звернення матриць, запрограмований у ряді стандартних програм апроксимації.
У матричній формі система (2.26) запишеться
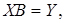 (2.30)
(2.30)
де X - вихідна матриця;
B - матриця вихідних значень параметрів;
Y - матриця вільних членів.
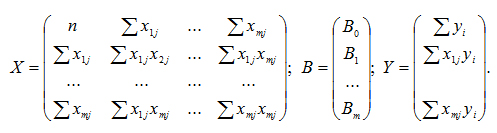 (2.31)
(2.31)
При вирішенні системи лінійних рівнянь матричним способом необхідно обчислити зворотну матрицю (X-1) і помножити її на праву і ліву частини рівняння (2.31), отримаємо
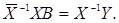 (2.32)
(2.32)
Так як 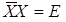 і
і 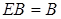 , то остаточний вираз для визначення матричним способом параметрів Biприйме вигляд:
, то остаточний вираз для визначення матричним способом параметрів Biприйме вигляд:
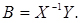 (2.33)
(2.33)
Контрольні запитання
1. Призначення кореляційно - регресійного аналізу.
2. Кореляційні і функціональні залежності.
3. Коефіцієнт кореляції та його граничні значення.
4. Формули обчислення парної і множинної коефіцієнтів кореляції.
5. Оцінка точності апроксимації нелінійної залежності.
6. Суть методу найменших квадратів.
7. Види парних регресій.
8. Способи лінеаризації нелінійних залежностей.
9. Множинна лінійна регресія.
10. Послідовність обчислення параметрів множинної регресії методом Крамера.
11. Послідовність обчислення параметрів множинної регресії матричним способом.