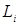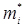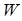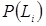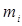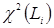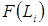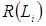3. ІМОВІРНІСНІ МОДЕЛІ
При вивченні технологічних процесів (technological process) автомобільного транспорту нерідко виникає необхідність обробки великих обсягів інформації, наданої у вигляді статистичних рядів. Наприклад, пробіг шин до заміни, величина зносу протектора шини у різних автомобілів на певному пробігу, величина люфту рульового управління автомобілів в процесі експлуатації та інші випадкові величини.
Випадковою величиною називається така величина, яка в результаті досвіду може прийняти те чи інше значення, яке з точністю не можна пе-редбачити до досвіду.
Всі випадкові величини діляться на дискретні і безперервні. Дискретна випадкова величина приймає фіксовані значення на відрізку [а, в]. Безперервна випадкова величина приймає на відрізку [а, в] будь-яке значення.
При обробці такої статистичної інформації визначаються числові характеристики і закон розподілу розглянутої випадкової величини.
3.1 Характеристики випадкових величин
Для кількісної оцінки випадкової однорідної величини (random variable) використовуються такі числові характеристики:
Середнє арифметичне випадкової величини служить характеристикою математичного сподівання розподілу випадкової величини і обчислюється за формулою:
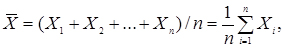 (3.1)
(3.1)
де X1,X2,...,Xn - значення елементів ряду;
n - число елементів ряду.
Статистична дисперсія характеризує розкид випадкової величини відносно її середнього значення. Вона обчислюється за формулою:
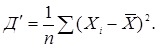 (3.2)
(3.2)
Середнє квадратичне відхилення (average deviation) служить мірою розсіювання випадкової величини відносно її середнього значення й обчислюється за формулою:
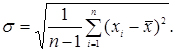 (3.3)
(3.3)
Коефіцієнт варіації ряду (coefficient of variation range) визначається ставленням 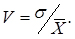 . За коефіцієнтом варіації наближено визначається закон розподілу випадкової величини, так при
. За коефіцієнтом варіації наближено визначається закон розподілу випадкової величини, так при 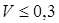 розподілення підкоряється нормальному закону, при
розподілення підкоряється нормальному закону, при 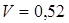 - закону розподілу Релея, а при
- закону розподілу Релея, а при 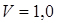 - експоненціальним (показового) закону розподілу.
- експоненціальним (показового) закону розподілу.
Статистична оцінка коефіцієнта асиметрії дає додаткову інформацію про форму розподілу випадкової величини (рис. 3.1). Асиметрія або скошеність обчислюється за формулою:
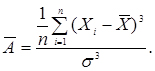 (3.4)
(3.4)
Статистична оцінка коефіцієнта ексцесу дає додаткову інформацію про форму розподілу випадкової величини (рис. 3.2).Ексцес, або гостровершиність обчислюється за формулою
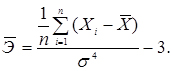 (3.5)
(3.5)
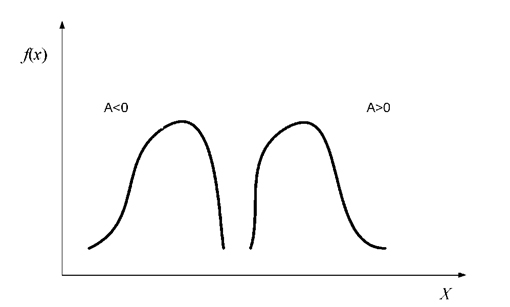
Рисунок 3.1 – Позитивна і негативна асиметрія
3.2 Закони розподілу випадкової величини
Між приватними значеннями випадкової величини і ймовірностями їх появи існує певна залежність. Зазначена залежність називається законом розподілу.

Рисунок 3.2 – Позитивний і негативний ексцеси
Закон розподілу випадкової величини можна задати у вигляді таблиці, графіка або формули.
Розрізняють закони розподілу дискретної випадкової величини і закони розподілу неперервної випадкової величини.
3.2.1 Закони розподілу дискретної випадкової величини
Основними ймовірностями закону розподілу дискретної випадкової величини є біноміальний закон і закон Пуассона.
Біноміальний закон розподілу (binomial distribution law).
Біноміальний розподіл виникає при виконанні наступних умов:
- в результаті одного випробування може з'явитися одне з двох протилежних подій A або 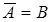 ;
;
- імовірності зазначених подій від досвіду до досвіду не змінюються і складають 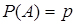 і
і 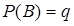 ;
;
- проводиться n незалежних випробувань.
При виконанні зазначених умов виникають різні комбінації таких подій, ймовірність появи яких визначається за формулою, званої біноміальним законом розподілу
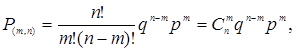 (3.6)
(3.6)
де n - число незалежних випробувань;
P(m,n) - імовірність того, що при n випробуваннях подія A з'явиться рівно m разів;
p і q - ймовірності появи відповідно подій A і B , де q=1-p;
Cmn- число сполучень із n елементів по m.
Для біноміального розподілу числових характеристик: математичне сподівання M(m) = пр і дисперсія Д(m) = прq виражаються за допомогою формул
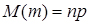 і
і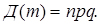
Розподіл Пуассона (Poisson distribution).
Розподіл Пуассона являє собою граничний випадок біноміального розподілу для умов, коли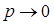 ;
;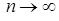 й
й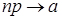 .
.
Перетворюючи вираз біноміального закону при наведених вище умовах, отримаємо формулу розподілу Пуассона:
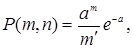 (3.7)
(3.7)
де n - число випробувань;
m - число появ події A m(=0,1,2...);
P(m,n) - імовірність того, що при n випробуваннях подія A з'явиться рівно m' раз;
a - параметр закону (a=np);
p - ймовірність появи події A в одному випробуванні.
У зв'язку з тим, що ймовірність появи окремих подій у розподілі Пуассона характеризується малою ймовірністю (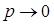 ), закон Пуассона називають законом рідкісних явищ.
), закон Пуассона називають законом рідкісних явищ.
Математичне сподівання M(m) і дисперсія Д(m) для розподілу Пуассона рівні і визначаються за виразом:
 (3.8)
(3.8)
Закон Пуассона описує:
- потік вимог у зону ремонту та ТО;
- потік заявок на запасні частини, вузли, агрегати;
- випадкове число відмов протягом фіксованого напрацювання.
Дискретна випадкова величина, крім формул 3.6 і 3.7, також може бути задана:
а) рядом розподілу ймовірності (табл. 3.1).
Таблиця 3.1 – Ряд розподілу ймовірності
Частота значення події A |
ma |
0 |
1 |
2 |
3 |
… |
m |
Ймовірності, що відповідають приватним значенням появи випадкової величини |
P(m,n) |
P(0,n) |
P(1,n) |
P(2,n) |
P(3,n) |
… |
P(m,n) |
б) багатокутником розподілу ймовірності появи події A (рис. 3.3).
в) графіком функції розподілу ймовірності.
На підставі ряду розподілу або багатокутника розподілу може бути побудований графік функції розподілу рис. 3.4.
Основні числові характеристики дискретної випадкової величини в цьому випадку визначаються за формулами
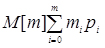 - математичне сподівання;
- математичне сподівання;
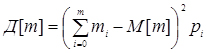 - дисперсія.
- дисперсія.
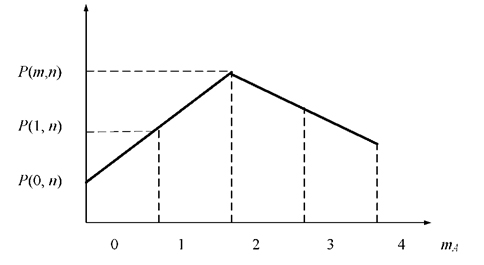
Рисунок 3.3 – Багатокутник розподілу ймовірності дискретної
випадкової величини
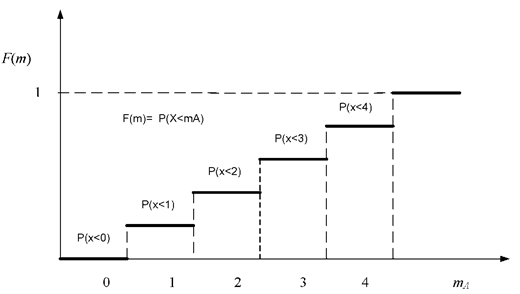
Рис. 3.4 – Графік розподілу ймовірності дискретної
випадкової величини
3.2.2 Закони розподілу неперервної випадкової величини
При описі безперервних випадкових величин виробничих процесів автомобільного транспорту широко використовуються такі імовірнісні закони:
- нормальний закон розподілу;
- закон рівномірної щільності;
- показовий (експонентний) закон розподілу;
- закони Вейбулла та ін.
Нормальний закон розподілу (normal distribution).
Нормальний закон розподілу записується так:
 (3.9)
(3.9)
де f(x) - щільність ймовірності розподілу неперервної випадкової величини;
xi - поточне значення випадкової величини (аргумент);.
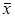 - математичне сподівання випадкової величини (середнє значення);
- математичне сподівання випадкової величини (середнє значення);
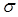 - середньоквадратичне відхилення випадкової величини;
- середньоквадратичне відхилення випадкової величини;
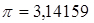 ;
;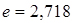 .
.
Графік щільності ймовірності розподілу випадкової величини нормального закону має вигляд рис. 3.5.
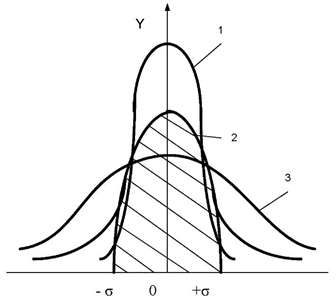
Рисунок 3.5 – Характер розсіювання кривої нормального
Розподілу
Нормальний закон розподілу може бути заданий функцією розподілу ймовірностей випадкової величини.
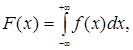 то
то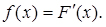 (3.10)
(3.10)
Числові характеристики закону визначаються формулами
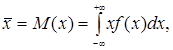 (3.11)
(3.11)
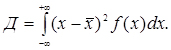 (3.12)
(3.12)
Для нормального закону розподілу випадкової величини укладаються на ділянці 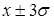 і називається правилом трьох сигм.
і називається правилом трьох сигм.
Для нормального закону розподілу має місце коефіцієнт варіації
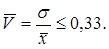 (3.13)
(3.13)
У галузі автомобільного транспорту нормальний закон описує:
- пробіг до капітального ремонту агрегатів і вузлів автомобіля;
- добові пробіги автомобілів;
- час на операції ТО і їх трудомісткості;
- напрацювання деталей з поступовими характером відмов;
- час на капітальний ремонт агрегатів і т.д.
Закон рівномірної щільності.
Закон рівномірної щільності записується так:
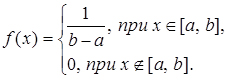 (3.14)
(3.14)
Графік щільності розподілу цього закону наведено на рис. 3.6.
Так як 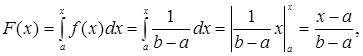
то при 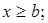 ;
; 
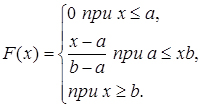 (3.15)
(3.15)
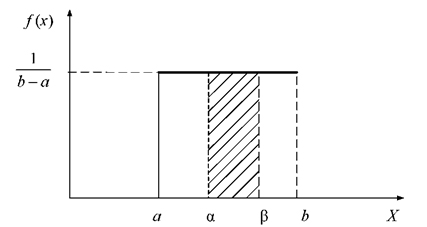
Рисунок 3.6 – Графік розподілу закону рівномірної щільності
Числові характеристики закону визначаються за такими формулами:
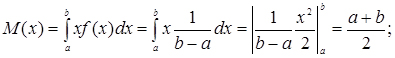 (3.16)
(3.16)
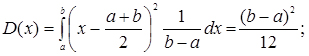 (3.17)
(3.17)
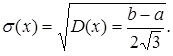 (3.18)
(3.18)
Ймовірність попадання випадкової величини X у відрізок 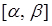 , де
, де 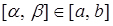 (див. рис. 3.6.) визначаються за формулою:
(див. рис. 3.6.) визначаються за формулою:
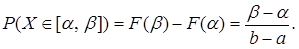 (3.19)
(3.19)
Рівномірний закон розподілу описує процеси пов'язані з роботою світлофорів, використовується в задачах масового обслуговування, при статистичному моделюванні процесів автомобільного транспорту.
Так, випадкова величина x , розподілена за рівномірним законом на відрізку [0, 1] називається «випадковими числами від 0 до 1», служить вихідним матеріалом для отримання випадкової величини з будь-яким законом розподілу.
Приклад. Потяги метрополітену йдуть регулярно з інтервалом 2 хв. Пасажири виходять на платформу в випадковий момент часу. Яка ймовірність того, що чекати пасажирові доведеться не більше півхвилини.
Знайти 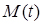 і
і 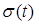 випадкової величиниt - часу очікування поїзда.
випадкової величиниt - часу очікування поїзда.
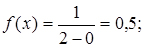
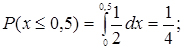
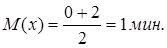
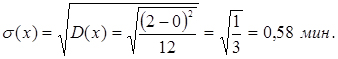
Показовий (експонентний) закон розподілу.
Показовий закон розподілу записується так
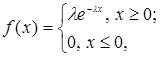 (3.20)
(3.20)
де 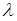 - параметр закону.
- параметр закону.
Так як 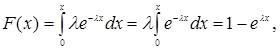 то
то
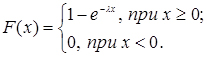
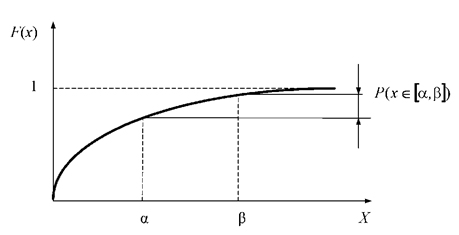
Графіки f(x) і F(x) наведено на рис. 3.7. та 3.8.
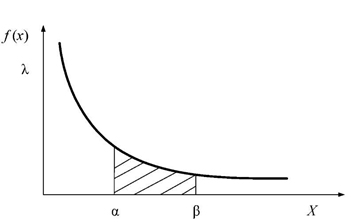
Рисунок 3.7 – Графічні залежності f(x) і F(x)
У теорії надійності F(x) - характеризує ймовірність розподілу відмов, R=1-F(x) - характеризує ймовірність справного стану виробу.
Числові характеристики закону обчислюються за формулами
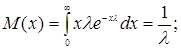 (3.21)
(3.21)
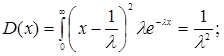 (3.22)
(3.22)
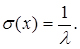 (3.23)
(3.23)
Ймовірність попадання випадкової величини в інтервал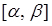 (див. рис. 3.7 і 3.8) визначається виразом
(див. рис. 3.7 і 3.8) визначається виразом
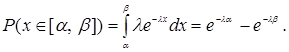 (3.24)
(3.24)
 (3.24)
(3.24)
Рисунок 3.8 – Ймовірність попадання випадкової величини в
Приклад. Час обслуговування автомобіля на СТОА розподілено по показовому закону з параметром 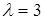 авт. год. Визначити скільки автомобілів буде обслуговано за час від t=0,13 до t=0,7.
авт. год. Визначити скільки автомобілів буде обслуговано за час від t=0,13 до t=0,7.
Рішення. 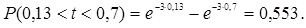
Експонентний закон зустрічається в заданих надійності та масового обслуговування.
Йому підпорядковуються:
- напрацювання деталей з раптовим характером відмов;
- проміжки часу між надходженнями автомобілів в зону ремонту;
- час відновлення автомобілів при поточному ремонті.
Закон Вейбулла.
Щільність розподілу ймовірності закону Вейбулла має вигляд
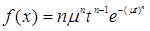 при
при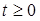 ,
,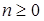 ,
,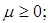 (3.25)
(3.25)
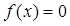 при
при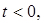 ,
, 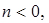 ,
, 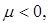
де t - випадкова величина (час, пробіг і т. д.);
n - параметр форми (при n=1 закон Вейбулла перетворюється на показовий закон, при n=2 - у закон Релея, при n=3,25 - у нормальний закон);
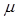 - параметр масштабу.
- параметр масштабу.
Отже, щільність розподілу Вейбулла задається двома параметрами n і 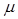 , що обумовлює широкий діапазон його застосування на практиці.
, що обумовлює широкий діапазон його застосування на практиці.
Розподіл Вейбулла знаходить широке застосування при дослідженні функціонування автотранспортних засобів. Добре описує поступові відмови виробів.
У деяких випадках замість 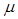 застосовують величину, оброблену за параметром масштабу
застосовують величину, оброблену за параметром масштабу  , тоді щільність ймовірності записується так:
, тоді щільність ймовірності записується так:
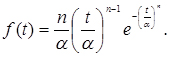 (3.26)
(3.26)
Графік щільності розподілу Вейбулла наведено на рис. 3.9. Функція розподілу закону Вейбулла має вигляд
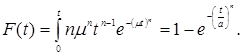 (3.27)
(3.27)
У теорії надійності крива функції розподілу F(t) характеризує ймовірність відмови вироби, а функція
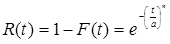 (3.28)
(3.28)
характеризує ймовірність справного стану виробу і називається кривою ресурсу.
При вирішенні завдань надійності доводиться обчислювати інтенсивність відмов виробів, яка в загальному випадку дорівнює відношенню щільності розподілу до ймовірності безвідмовної роботи виробу
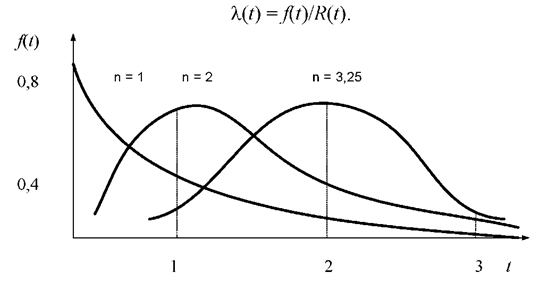
Рисунок 3.9 – Графіки щільності розподілу
Очевидно, що якщо в міру перебігу часу ймовірність справної роботи вироби зменшується, то і значення інтенсивності відмови вироби змінюється (зростає) (рис. 3.10).
Формули математичного сподівання і дисперсії закону Вейбулла мають вигляд:
 (3.29)
(3.29)
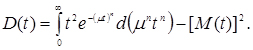 (3.30)
(3.30)
Зазначені інтеграли легко обчислюються за допомогою гамма-функції
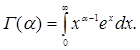 (3.31)
(3.31)
Значення гамма - функції Ейлера залежно від параметра 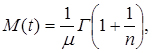 наведено в таблиці 3 (Додатки).
наведено в таблиці 3 (Додатки).
Перетворюючи вираження (3.29) і (3.30) до вигляду, зручного для застосування гамма - функції Ейлера, одержимо:
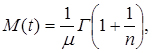 (3.32)
(3.32)
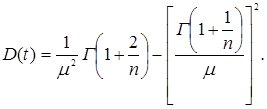 (3.33)
(3.33)
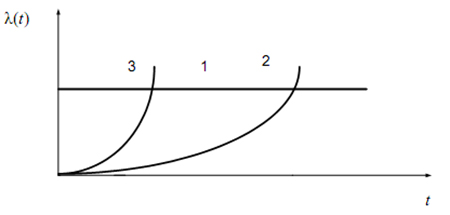
1 - показового закону; 2 - закону Вейбулла; 3 - нормального закону
Рис. 3.10 - Криві інтенсивності відмов
Формула для обчислення коефіцієнта варіації в цьому випадку приймає вигляд:
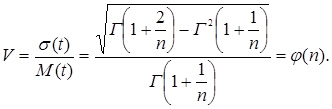 (3.34)
(3.34)
Коефіцієнт варіації є функцією параметра форми закону (n) . У свою чергу, параметр форми закону n є функцією коефіцієнта варіації V:
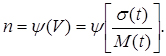 (3.35)
(3.35)
Отже, якщо відомі M(t) і 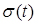 закону Вейбулла, то можемо визначити значення параметра форми n і на підставі цього визначити параметр масштабу
закону Вейбулла, то можемо визначити значення параметра форми n і на підставі цього визначити параметр масштабу 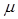 .
.
3.3 Генеральна і вибіркова сукупності
Завдання, що виникають при вивченні процесів автомобільного транспорту, вимагають знань основних положень теорії ймовірностей і математичної статистики.
Якщо математична статистика займається розробкою методів збору та обробки результатів спостережень випадкових процесів, то теорія ймовірностей вивчає їх закономірності.
При вирішенні задач математичної статистики і теорії ймовірностей доводиться стикатися з поняттям генеральної і вибіркової сукупностей.
Генеральною сукупністю називають сукупність всіх об'єктів (елементів), що підлягають вивченню. Очевидно, що піддавати дослідженню всю генеральну сукупність важко або недоцільно. У зв'язку з цим з генеральної сукупності витягують лише деяку її частину, звану вибірковою сукупністю (вибіркою).
Використовуючи методи математичної статистики (mathematical statistics), можливо визначити числові характеристики вибіркової сукупності. І перенісши їх за певними правилами на генеральну сукупність, оцінити числові характеристики останньої.
Отже, нехай потрібно дослідити деяку генеральну сукупність «Г.с.» (рис. 3.11), яка характеризується параметрами: М(ч) - математичне сподівання; D(x) - дисперсія; 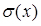 - середньоквадратичне відхилення; f(x) - щільність розподілу; F(x) - функція розподілу.
- середньоквадратичне відхилення; f(x) - щільність розподілу; F(x) - функція розподілу.
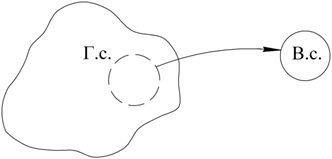
Рисунок 3.11 – Схема процесу вибірки
Безпосередньо обчислити їх неможливо. Однак можна оцінити (прийняти) за даними вибіркової сукупності. Для чого з генеральної сукупності винесемо вибірку «В.с.», для якої методами математичної статистики можемо обчислити: X - середнє арифметичне; D*(x) - статистична дисперсія; 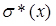 - статистично середнє квадратичне відхилення; W*(x) - відносна частота; F*(x) - статистична (експериментальна) функція розподілу.
- статистично середнє квадратичне відхилення; W*(x) - відносна частота; F*(x) - статистична (експериментальна) функція розподілу.
Знайшовши потрібні нам числові характеристики вибіркової сукупності, можемо перенести їх за певних умов на всю генеральну сукупність, т.т, прийняти:
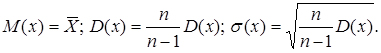 (3.36)
(3.36)
3.4 Обробка дослідних даних вибіркової сукупності
Нехай маємо добрий обсяг вибірки (статистичний ряд). Порядок обробки його наступний:
- зареєстровані значення розглянутого ознаки Xi розташувати в зростаючому порядку;
- знайти найбільше Xmax і найменше Xmin значення параметра;
- визначити розмах вимірювання значень параметра:
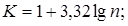 (3.37)
(3.37)
- обчислити число інтервалів K в залежності від обсягу вироблення n:
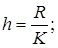 (3.38)
(3.38)
- визначити ширину часткового інтервалу h:
- визначити межі інтервалів, для чого встановити нульове (крайнє) значення інтервалу X0:
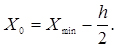 (3.39)
(3.39)
Наступні межі інтервалів визначаються послідовним додатком ширини інтервалу до h попереднього значення кордону:
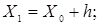 ;
;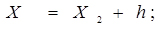 і т.д. до тих пір поки Xk не буде більше Xmax;
і т.д. до тих пір поки Xk не буде більше Xmax;
- Визначити число елементів значень ознак, що потрапили в i- й інтервал (цю величину називають дослідною частотою m*i, даного інтервалу);
- Результати розрахунку звести в таблицю 3.2, яку називають інтервальним варіаційним рядом.
Відносну величину частоти називають частостей i- го інтервалу Wi
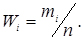 (3.40)
(3.40)
Накопичення частости WH виходить шляхом послідовного додавання частости Wi, чергового інтервалу
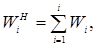 (3.41)
(3.41)
для останнього інтервалу:
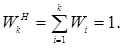 (3.42)
(3.42)
Таблиця 3.2 – Зведена таблиця обробки вибіркових даних
Номер інтервалу |
Ширина інтервалу |
Середина інтервалу |
Частота
|
Частость
|
Накопичена частость |
1 |
X1 - X0 |
|
m*1 |
W1 |
WHi |
2 |
X2 - X1 |
|
m*2 |
W2 |
WH1 |
… |
… |
… |
… |
… |
… |
k |
Xk - Xk-1 |
|
m*k |
Wk |
WHk |
Основні числові характеристики для інтервального варіаційного ряду обчислюються за такими формулами:
- середнє арифметичне:
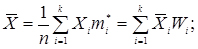 (3.43)
(3.43)
- статистична дисперсія:
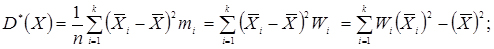 (3.44)
(3.44)
- середньоквадратичне відхилення:
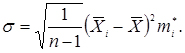 (3.45)
(3.45)
Графічне вираження закону розподілу можна представити у вигляді гістограми і похилої (кумулятивної) кривої (рис. 3.12 і 3.13).
Гістограма являє собою набір прямокутників, підставою кожного є довжина часткового інтервалу, а висота m*i або Wi (рис.3.12).
За побудованою гістограмою призначається теоретичний закон розподілу випадкової величини f(x) , для якого за формулою
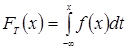 (3.46)
(3.46)
визначається теоретична функція розподілу FT(x).
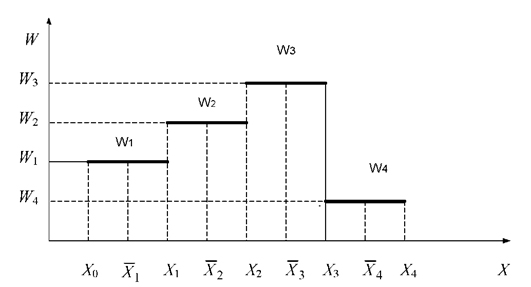
Рисунок 3.12 – Гістограма розподілу ознаки
Кумулятивна крива (сumulative curve) будується за накопиченим частостей WHi, вона відповідає дослідній функції розподілу ознаки 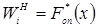 (рис.*3.13). Відповідність дослідної
(рис.*3.13). Відповідність дослідної 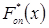 і теоретичної F(x) функції розподілу може бути оцінений за допомогою критерієм згоди.
і теоретичної F(x) функції розподілу може бути оцінений за допомогою критерієм згоди.
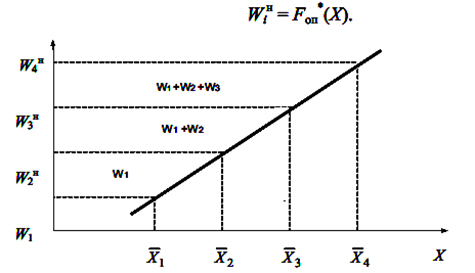
Рисунок 3.13 – Графік дослідної функції розподілу ознаки (кумулятивна крива)
3.5 Оцінка гіпотез
При статистичній обробці дослідних даних одне з найважливіших завдань - це завдання перевірки гіпотез про приналежність досвідчених даних (гістограм) до того чи іншого ймовірному закону.
При висуванні та прийнятті зазначених гіпотез виникають наступні чотири випадки:
1. Гіпотеза H0 вірна і приймається.
2. Гіпотеза H0 вірна, але помилково відкидається. Виниклу при цьому помилку називають помилкою першого роду, а ймовірність її появи називають рівнем значущості і позначають 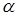 .
.
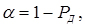 (3.47)
(3.47)
де PД - довірча ймовірність.
3. Гіпотеза H0 не вірна і відкидається.
4. Гіпотеза H0 не вірна, але помилково приймається. Виниклу при цьому помилку називають помилкою другого роду, а ймовірність її появи позначають 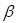 .
.
Для вирішення зазначеної задачі запропоновані відповідні критерії і заздалегідь, при заданому рівні значущості 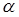 , підраховані і складені таблиці, в яких поміщені критичні (табличні) значення вказаних критеріїв.
, підраховані і складені таблиці, в яких поміщені критичні (табличні) значення вказаних критеріїв.
При практичній перевірці розглянутих гіпотез відбувається зіставлення досвідчених значень критерій Kon з табличним значенням критерію Kkp(Kтабл) і далі залежно від співвідношення Kon <> Kkp приймають або відкидають висунуту гіпотезу.
Критерії статистичної оцінки гіпотез (сriterion for statistical evaluation of hypotheses).
Розглянемо порядок статистичної перевірки правдоподібності гіпотези про приналежність дослідних даних до заданого виду імовірнісного закону. Вирішення цього завдання проводиться в два етапи:
- за видом гістограми (багатокутника) або, виходячи з фізичної сутності даного явища, роблять попереднє судження, тобто висувається гіпотеза про приналежність дослідних даних до конкретного ймовірного закону;
- застосовуючи метод моментів, роблять перевірку правдоподібності висунутої гіпотези.
Суть методу моментів полягає в тому, що параметри зглажуючого закону повинні зберегти основні риси статистичного розподілу, тобто щоб була рівність математичного сподівання і дисперсії статистичного та зглажуючих розподілів.
Перевірка правдоподібності гіпотези про приналежність дослідних даних до заданого виду імовірнісного закону може проводитися за допомогою критеріїв: Пірсона, Колмогорова, Романовського, Фішера, Кохрена, Стьюдента та ін.
1. Критерій x2 Пірсона. Критерій x2 Пірсона записується у вигляді наступної альтернативної умови:

x2 обчислюється за формулою
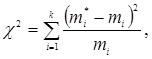 (3.48)
(3.48)
де r - число ступенів свободи, r = k - s;
k - число інтервалів гістограми;
s - число накладених зв'язків.
У число накладених зв'язків входять поняття;
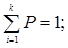
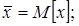
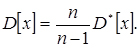 (3.49)
(3.49)
Значення ймовірностей 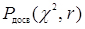 , обчислені в залежності від числа ступенів свободи r і досвідченого значення x2 наведено в табл. 2 дод. 1.
, обчислені в залежності від числа ступенів свободи r і досвідченого значення x2 наведено в табл. 2 дод. 1.
2. Критерій Романовськогого.

де x2 - критерій Пірсона;
K - число інтервалів.
3. Критерій Колмогорова.
Критерій Колмогорова записується у вигляді альтернативної умови:
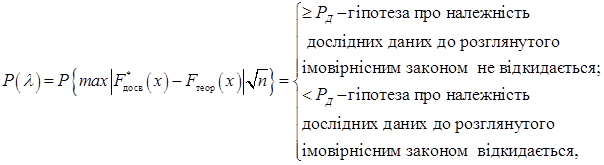
де n - обсяг вибірки (число всіх випробувань);
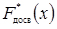 - дослідне значення функції розподілу;
- дослідне значення функції розподілу;
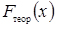 - теоретичне значення функції розподілу;
- теоретичне значення функції розподілу;
PД- довірча ймовірність.
Для критерію Колмогорова є заздалегідь складена таблиця (табл. 1, Додатки).
3.6 Приклади обробки дослідних даних ймовірносними законами
3.6.1 Обробка даних показовим законом розподілу
Математичною моделлю виникнення показового (експоненціального) закону (exponential law) є такі умови, коли поодинокі пошкодження призводять до раптової відмови складного виробу, наприклад, перегорання лампочки, прокол шини, поломка колінчастого валу та ін.
Щільність ймовірності показового закону розподілу така:
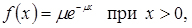
де x - випадкова величина;
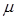 - параметр закону, який представляє інтенсивність відмов;
- параметр закону, який представляє інтенсивність відмов;
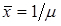 - середній ресурс.
- середній ресурс.
Розглянемо на прикладі порядок згладжування експериментальних даних показовим законом стосовно до теорії надійності.
Статистичними спостереженнями встановлено, що у автомобіля
КрАЗ-6510 лампочки покажчиків повороту перегоріли на пробігу (тис. км):
8,3; 18,4; 27,8; 47,1; 74; 19,7; 3; 11,8; 17,4; 14; 9,7; 34,1; 4; 31,9; 42; 7,3; 85,2; 39,6; 53; 57; 21,8; 58,4; 38,1.
Потрібно:
1. Встановити закон, якому підпорядковується досліджуване явище, і перевірити правдоподібність зробленої гіпотези за критерієм згоди Пірсона при рівні значущості 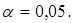
2. Розрахувати і побудувати теоретичну криву частот відмови лампочок.
3. Розрахувати і побудувати криві імовірності відмови та ймовірності справної роботи лампочок.
Розв’язок:
1. Визначаємо величину інтервалу варіаційного ряду
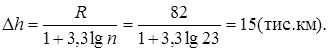
2. Будуємо гістограму розподілу частот відмови лампочок (рис. 3.14.).
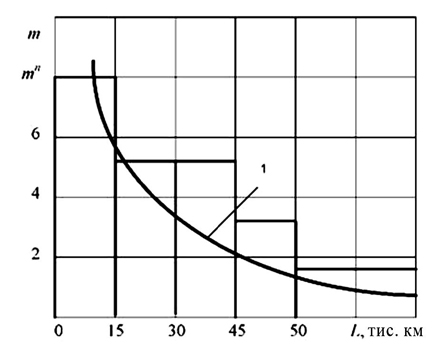
Рисунок 3.14 – Гістограма розподілу частот відмови
За характером гістограми розподілу частот відмови лампочок припускаємо, що їх відмова слідує показовому закону.
3. Визначаємо середній ресурс лампочок
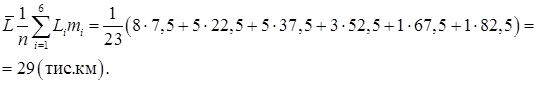
4. Розраховуємо інтенсивність відмови лампочок
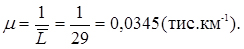
5. Обчислюємо теоретичні ймовірності попадання в розряди;
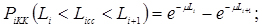
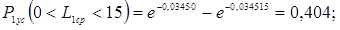
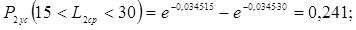
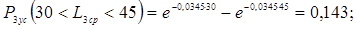
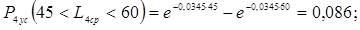
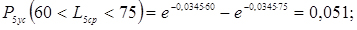
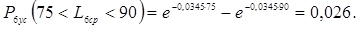
6. Знаходимо нормуючий множник
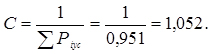
7. Обчислюємо виправлені ймовірності
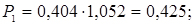 ;
; 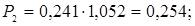
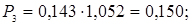 ;
; 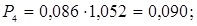
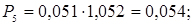 ;
; 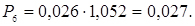
8. Визначаємо теоретичні частоти
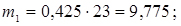 ;
; 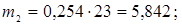 ;
; 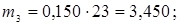
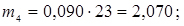 ;
; 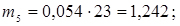 ;
; 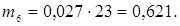
9. Обчислюємо значення критерію згоди x2 Пірсона
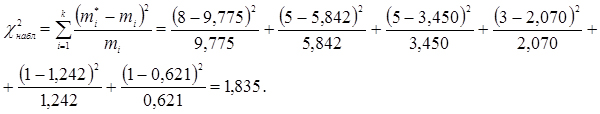
За табл. 2 (Додатки) знаходимо критичне значення критерію x2 для α = 0,05 і S = 4:
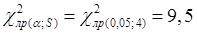 ;
; 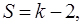
де k - число стовпців гістограми.
Якщо  , то гіпотеза про приналежність експериментальних даних до показового закону розподілу приймається.
, то гіпотеза про приналежність експериментальних даних до показового закону розподілу приймається.
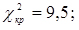 ;
; 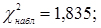 ;
; 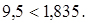
Результати розрахунку показового закону розподілу заносимо в табл. 3.3.
10. На рис. 3.14 по даними рядка 6 будуємо теоретичний закон розподілу відмови лампочок (крива 1).
11. За даними рядків 8 і 9 будуємо криві імовірності відмови (крива 1) та ймовірності справної роботи лампочок (крива 2) (рис. 3.15).
Таблиця 3.3 – Результати розрахунку показового закону розподілу
№ рядка |
Параметр |
Номер розряду |
Примітка |
|
||||||
1 |
2 |
3 |
4 |
5 |
6 |
|
||||
1 |
Межі розрядів, |
0 |
15 |
30 |
45 |
60 |
75 |
|
||
2 |
Середини розрядів, |
7,5 |
22,5 |
37,5 |
52,5 |
67,5 |
82,5 |
|
||
3 |
Досвідчені частоти, |
8 |
5 |
5 |
3 |
1 |
1 |
|
||
4 |
Імовірність усіченого розподілу, |
0,404 |
0,241 |
0,143 |
0,086 |
0,051 |
0,026 |
|
||
5 |
Виправлені ймовірності, |
0,425 |
0,254 |
0,150 |
0,090 |
0,054 |
0,027 |
|
||
6 |
Теоретичні частоти, |
9,775 |
5,842 |
3,450 |
2,070 |
1,242 |
0,621 |
|
||
7 |
Критерій згоди Пірсона, |
0,322 |
0,121 |
0,696 |
0,418 |
0,047 |
0,231 |
|
||
8 |
Функція ненадійності, |
0,425 |
0,679 |
0,829 |
0,919 |
0,973 |
1,000 |
|
||
9 |
Функція надійності, |
0,575 |
0,321 |
0,171 |
0,081 |
0,027 |
0,000 |
|
||
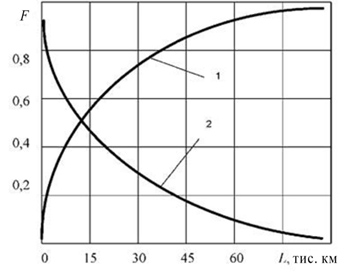
Рисунок 3.15 – Графік розподілу відмов і справної роботи лампочок
3.6.2 Обробка даних нормальним законом розподілу
Математичною моделлю виникнення нормального закону розподілу служить дія великої кількості різних незалежних факторів або слабо залежних джерел.
Стосовно до математичної теорії надійності закон добре описує поступові відмови, викликані ладу їх окремих елементів.
Щільність ймовірності нормального закону розподілу наступна:
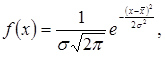 (3.50)
(3.50)
де x - випадкова величина;
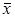 - середнє значення розглянутої випадкової величини;
- середнє значення розглянутої випадкової величини;
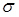 - середнє квадратичне відхилення, що характеризує розкид випадкової величини відносно її середнього значення.
- середнє квадратичне відхилення, що характеризує розкид випадкової величини відносно її середнього значення.
Розглянемо на прикладі порядок згладжування експериментальних даних нормальним законом розподілу стосовно до дослідження технічного стану автомобілів.
У 79 автомобілів ГАЗ-3110 виміряно люфт рульового управління:
9; 18; 7; 12; 14; 6; 10; 9; 16; 6; 14; 7; 14; 6; 11; 12; 13; 7; 7; 18; 18; 8; 10; 6; 10; 8; 9; 10; 10; 9; 8; 9; 16; 9; 11; 12; 14; 14; 15; 26; 9; 17; 9; 11; 9; 10; 8; 18; 16; 15; 8; 10; 17; 16; 16; 12; 19; 12; 14; 20; 19; 16; 12; 12; 11; 14; 14; 14; 17; 7; 4; 5; 6; 5; 5; 4; 7; 6; 6 град.
Потрібно: 1. Встановити закон, якому підпорядковується розподіл люфту рульового керування автомобіля ГАЗ-24Т, і перевірити правдоподібність зробленої гіпотези за критерієм згоди Пірсона при рівні значущості 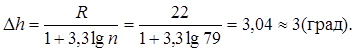 і за критерієм згоди Романовського.
і за критерієм згоди Романовського.
2. Побудувати графіки дослідної та теоретичної інтегральних функцій.
Розв’язок: 1. Визначаємо величину інтервалу варіаційного ряду
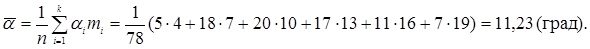
2. Будуємо гістограму розподілу люфту рульового керування автомобіля ГАЗ-24Т (рис. 3.16.).
Люфт рульового управління, рівний 26 град, різко відрізняється від інших експериментальних даних. Перевіримо приналежність його до даній вибірці за правилом трьох середніх квадратичних відхилень.
3. Обчислюємо середнє арифметичне значення люфту рульового управління:
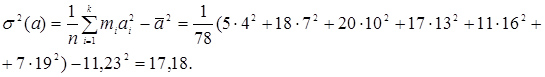
4. Обчислюємо дисперсію:

Рисунок 3.16 – Гістограма розподілу ознаки
4.1. Середнє квадратичне відхилення люфту рульового керування
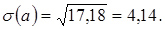
5. Визначаємо межі допустимого розкиду люфту рульового управління щодо його середнього значення.
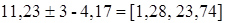
Отже, люфт рульового керування 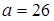 є аномальним і повинен бути виключений з подальшого аналізу.
є аномальним і повинен бути виключений з подальшого аналізу.
6. Виключивши аномальне значення люфту рульового управління з вибірки, визначаємо величину інтервалу варіаційного ряду:
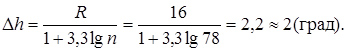
7. Будуємо повторно гістограму розподілу люфту рульового управління (рис. 3.17).
8. Розраховуємо ймовірності попадання в розряди
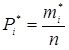 (3.51)
(3.51)
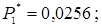 ;
; 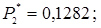 ;
; 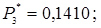
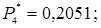 ;
; 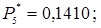 ;
; 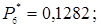
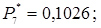 ;
; 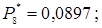 ;
; 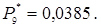
9. Записуємо формулу щільності ймовірності нормального закону розподілу, підставляючи в неї значення 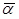 і
і 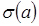 :
:
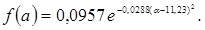
10. Розраховуємо значення функції f(a) для середин розрядів гістограми
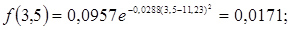
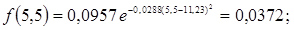
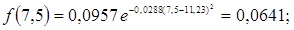
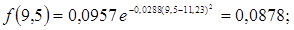
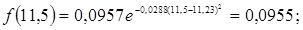
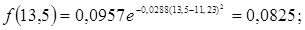
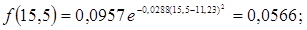
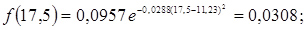
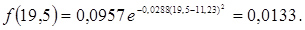
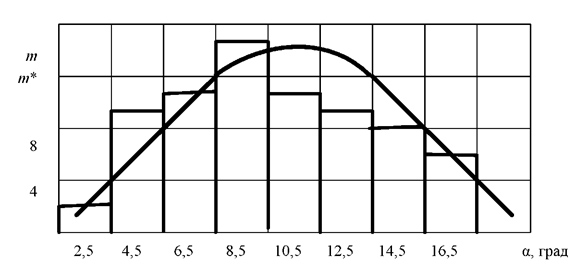
Рисунок 3.17 – Гістограма розподілу люфту рульового керування
11. Визначаємо нормуючий множник
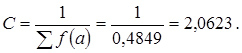
12. Розраховуємо теоретичні ймовірності попадання в розряди 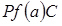
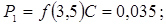 ;
; 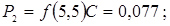
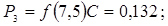 ;
; 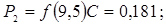
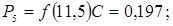 ;
; 
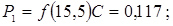 ;
; 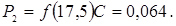
13. Розраховуємо теоретичні частоти потрапляння в розряди
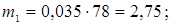 ;
;  ;
; 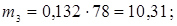
 ;
; 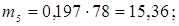 ;
; 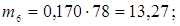
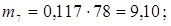 ;
; 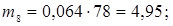 ;
; 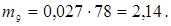
14. Обчислюємо значення критерію x2 Пірсона
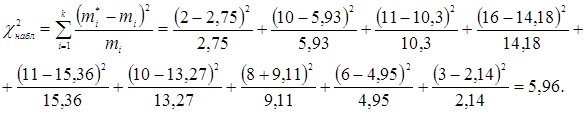
За табл. 2 (Додатки) знаходимо критичне значення критерію x2 для a = 0,05 і S = 6
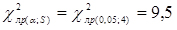 ;
; 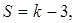
де k - число стовпців гістограми.
Якщо 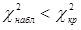 , то гіпотеза про належність експериментальних даних до нормального закону розподілу приймається, в іншому випадку - відхиляється.
, то гіпотеза про належність експериментальних даних до нормального закону розподілу приймається, в іншому випадку - відхиляється.
15. Перевіряємо гіпотезу про приналежність експериментальних даних до нормального закону розподілу за критерієм згоди Романовського.
Якщо 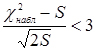 , то гіпотеза приймається:
, то гіпотеза приймається:

Гіпотеза про приналежність експериментальних даних до нормального закону розподілу за критерієм Романовського приймається. Результати розрахунку нормального закону розподілу заносимо в табл. 3.4.
16. За даними рядків 9 і 10 табл. 3.4 будуємо графіки дослідної 1 і теоретичної 2 інтегральних функцій (рис. 3.18).
3.6.3 Обробка даних за законом Вейбулла
Порядок перевірки гіпотези про приналежність дослідних даних до закону Вейбулла розглянемо на прикладі.
Приклад. Досліджується закон розподілу довжини пробігу ножного гальма автомобілів МАЗ-6430 до його відмови.
Статистичними спостереженнями було зафіксовано 29 результатів, які представлені інтервальним варіаційним рядом (табл. 3.5).
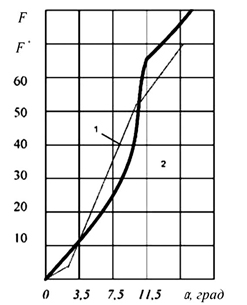
Рисунок 3.18 – Графіки інтегральних функцій
Таблиця 3.4 – Результати розрахунку нормального закону розподілу
№ рядка |
Параметр |
Номер розряду |
Примітка |
||||||||
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|||
1 |
Межі розрядів, |
2,5 |
4,5 |
6,5 |
8,5 |
10,5 |
12,5 |
14,5 |
16,5 |
18,5 |
|
2 |
Середини розрядів, |
3,5 |
5,5 |
7,5 |
9,5 |
11,5 |
13,5 |
15,5 |
17,5 |
19,5 |
|
3 |
Дослідні |
2 |
10 |
11 |
16 |
11 |
10 |
8 |
7 |
3 |
78 |
4 |
Дослідні ймовірності |
0,0256 |
0,1282 |
0,1410 |
0,2051 |
0,1410 |
0,1282 |
0,1026 |
0,0897 |
0,0385 |
0,9999 |
5 |
Значення функції |
0,0171 |
0,0372 |
0,0641 |
0,0878 |
0,0955 |
0,0825 |
0,0566 |
0,0308 |
0,0133 |
0,4849 |
6 |
Теоретичні ймовірності |
0,035 |
0,077 |
0,132 |
0,181 |
0,197 |
0,170 |
0,117 |
0,064 |
0,027 |
1,000 |
7 |
Теоретичні частоти |
2,75 |
5,98 |
10,31 |
14,13 |
15,36 |
13,27 |
9,10 |
4, 95 |
2,14 |
77, 98 |
8 |
Квадрати відхилень |
0,28 |
1,62 |
0,04 |
0,22 |
1,73 |
1,07 |
0,15 |
0,60 |
0,25 |
5,96 |
9 |
Накопичені досвідчені частоти |
2 |
12 |
23 |
39 |
50 |
60 |
68 |
75 |
78 |
|
10 |
Накопичені теоретичні частоти |
2,75 |
8,73 |
19,04 |
33,17 |
48,53 |
61,80 |
70,90 |
75,85 |
77,99 |
|
Таблиця 3.5 – Інтервальний варіаційний ряд
Номер інтервалу, |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
Межі інтервалу, |
0 - 10 |
10- 20 |
20- 30 |
30- 40 |
40- 50 |
50- 60 |
60- 70 |
70- 80 |
80- 90 |
90- 100 |
100- 110 |
110- 120 |
Число відмов |
9 |
14 |
18 |
7 |
9 |
9 |
4 |
4 |
2 |
1 |
1 |
1 |
Потрібно: 1. Встановити закон, якому слід розглядається явище і перевірити правдоподібність прийнятої гіпотези при рівні значущості .
2. Побудувати криву ймовірності виходу вироби з ладу і криву ймовірності справної роботи (криву ресурсу). Рішення: 1. Обчислюємо досвідчені відносні частоти виходу вироби з ладу по інтервалах напрацювання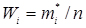 :
:
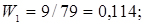 ;
;  і т.д.
і т.д.
Результати рахунки заносимо в табл. 3.5 за даними рядка 4 будуємо гістограму розподілу ознаки (рис. 3.19).
Таблиця 3.5 – Статистична таблиця довжини пробігу ножного гальма автомобілів МАЗ-6430 до його виходу з ладу
№ п/п |
Номер інтервалу |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
1 |
Межі інтервалу |
0 - 10 |
10 - |
20 - |
30 - 40 |
40 - 50 |
50 - 60 |
60 - 70 |
70 - 80 |
80 - 90 |
90 - 100 |
100 - 110 |
110 - 120 |
2 |
Середини інтервалів, |
5 |
15 |
25 |
35 |
45 |
55 |
65 |
75 |
85 |
95 |
105 |
115 |
3 |
Дослідні частоти, |
9 |
14 |
18 |
7 |
9 |
9 |
4 |
4 |
2 |
1 |
1 |
1 |
4 |
Дослідні частости, |
0,144 |
0,172 |
0,228 |
0,089 |
0,114 |
0,014 |
0,050 |
0,050 |
0,025 |
0,013 |
0,013 |
0,013 |
5 |
Теоретичні ймовірності, |
0,140 |
0,179 |
0,167 |
0,144 |
0,117 |
0,085 |
0,058 |
0,040 |
0,028 |
0,020 |
0,012 |
0,01 |
6 |
Теоретичні частоти, |
11 |
14 |
13 |
11,3 |
9,2 |
6,8 |
4,5 |
3,2 |
2,2 |
1,6 |
1,0 |
1,0 |
7 |
Додатки критерію Пірсона, |
0,363 |
0 |
1,192 |
1,63 |
0,04 |
0,74 |
0,055 |
0,20 |
0,018 |
0,22 |
0 |
0 |
8 |
Теоретична функція розподілу, |
0,140 |
0,319 |
0,486 |
0,630 |
0,747 |
0,832 |
0,890 |
0,930 |
0,958 |
0,978 |
0,99 |
1,0 |
9 |
Ймовірність справної роботи, |
0,860 |
0,681 |
0,514 |
0,370 |
0,253 |
0,168 |
0,110 |
0,070 |
0,042 |
0,022 |
0,01 |
0 |
Розглядаємо гістограму і робимо припущення, тобто висуваємо гіпотезу, що досліджуване явище - довжина пробігу ножного гальма на автомобілях МАЗ-500 до його відмови розподілена за законом Вейбулла:
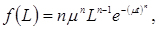 (3.52)
(3.52)
де n і 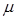 - відповідно параметр форми і параметр масштабу.
- відповідно параметр форми і параметр масштабу.
2. Обчислюємо статистичне математичне сподівання пробігу виробу:
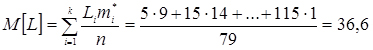 тис. км.
тис. км.
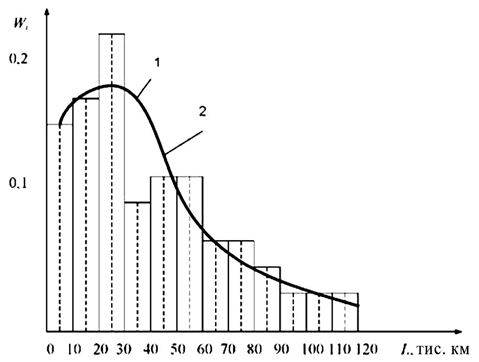
Рисунок 3.19 – Гістограма розподілу довжини пробігу ножного гальма автомобілів МА3-6430 до його виходу з ладу (1) і крива закону Вейбулла (2)
3. Обчислюємо статистичну дисперсію
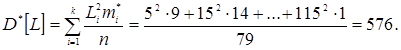
4. Знаходимо незміщене середньоквадратичне відхилення:
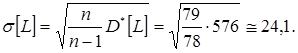
5. Знаходимо коефіцієнт варіації
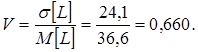
6. У таблиці 4 (Додатки) для знайденого коефіцієнта V = 0,660 знаходимо значення першого параметра закону (параметр форми, рівний 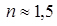 ).
).
7. Знаходимо другий параметр закону (параметр масштабу) за формулою
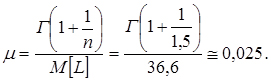
Для обчислення значення гамма - функції Ейлера використані дані таблиці 3 (Додатки).
Значення зворотного параметра масштабу становить

8. Обчислюємо теоретичні ймовірності попадання випадкової величини в інтервали за формулою
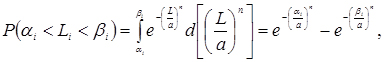
де 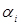 і
і 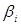 - відповідно ближній і дальній межі інтегрування;
- відповідно ближній і дальній межі інтегрування; 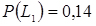 ;
; 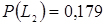 і т.д. (Див. рядок 5 табл. 3.5).
і т.д. (Див. рядок 5 табл. 3.5).
На основі даних рядка 5 наносимо на гістограму згладжує її теоретичну криву закону Вейбулла (див. рис. 3.19).
9. Обчислюємо теоретичні частоти:
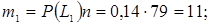
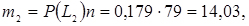
і т.д. (Див. рядок 6 табл. 3.5).
10. Обчислюємо доданки критерії Пірсона
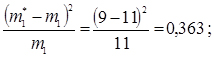 ;
; 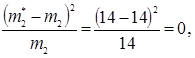 і т.д.
і т.д.
Підсумовуючи доданки критерію Пірсона, отримуємо:
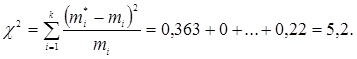
Перевіряємо правдоподібність прийнятої гіпотези про приналежність дослідних даних до закону Вейбулла.
За критерієм Пірсона:
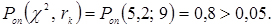
Відтак, за критерієм Пірсона при рівні значущості гіпотеза про приналежність дослідних даних до закону Вейбулла не відкидається.
За критерієм Романовського:
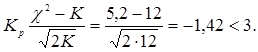
Як бачимо, за критерієм Романовського гіпотеза про приналежність дослідних даних до закону Вейбулла не відкидається.
12. Для побудови кривої ймовірностей відмови вироби F(L) і протилежної їй кривої (кривої ресурсу R(l)) скористаємося формулами:
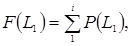 (3.53)
(3.53)
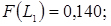 ;
; 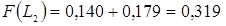 і т.д. (див. рядок 8 табл. 3.5).
і т.д. (див. рядок 8 табл. 3.5).
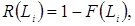 (3.54)
(3.54)
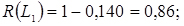 ;
; 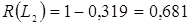 (див. рядок 9 табл. 3.5).
(див. рядок 9 табл. 3.5).
За даними рядків 8 і 9 табл. 3.5 будуємо графіки F(L) і R(L) (рис. 3.20).
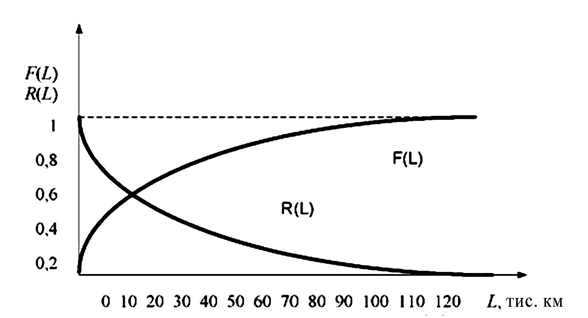
Рисуное 3.20 – Графік ймовірностей відмови виробу F(L) і кривої ресурсу R(L)
Контрольні запитання
1. Дайте визначення дискретної і неперервної випадкової величини.
2. Перерахуйте основні характеристики випадкових величин.
3. Особливості біноміального закону розподілу.
4. Особливості закону Пуассона.
5. Особливості нормального закону розподілу.
6. Особливості закону рівномірної щільності.
7. Особливості показового закону розподілу.
8. Особливості закону Вейбулла.
9. Дайте визначення генеральної і вибіркової сукупності.
10. Основні характеристики вибіркової сукупності і способи їх обчислення.
11. Основні характеристики генеральної сукупності і способи їх обчислення.
12. Дайте визначення поняттю «інтервальний варіаційний ряд».
13. Що таке гістограма і з якою метою вона будується?
14. Особливості критерію згоди - Пірсона.
15. Особливості критерію згоди Романовського.
16. Особливості критерію згоди Колмогорова.
17. Послідовність обробки дослідних даних показовим законом.
18. Послідовність обробки дослідних даних нормальним законом.
19. Послідовність обробки дослідних даних законом Вейбулла.
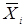
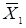
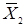
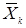
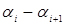
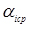
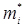
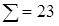
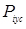
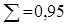
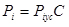
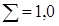
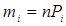
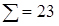
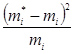
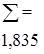
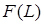
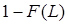
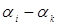
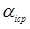
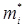
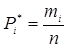
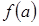
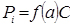
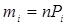
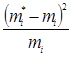
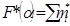
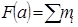
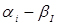 , тис. км
, тис. км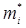 , в інтервалі
, в інтервалі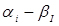 , тис. км
, тис. км