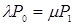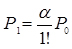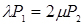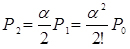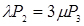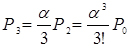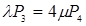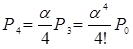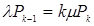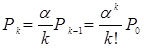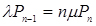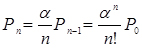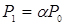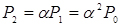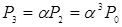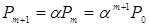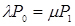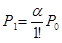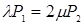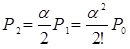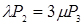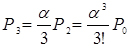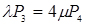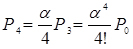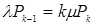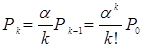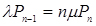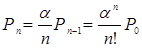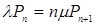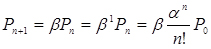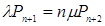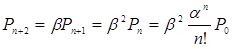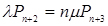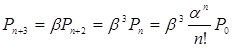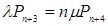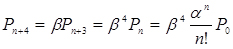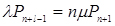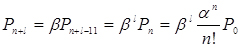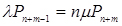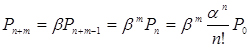4 ОСНОВИ МОДЕЛЮВАННЯ ВИПАДКОВИХ ПРОЦЕСІВ
4.1 Класифікація випадкових процесів
Випадковим процесом X(t)(random process) називається процес, значення якого при будь-якому фіксованому t=t0 є випадковою величиною X(t0).
Випадкова величина X(T0), в яку звертається випадковий процес при t=t0 називається перетином випадкового процесу, відповідним даному значенню аргументу t (рис. 4.1, 4.2).
Випадковий процес записується у вигляді функції двох аргументів - часу t і елементарної події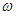 
; 
; 
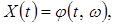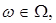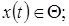(4.1)
де 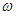- елементарна подія, що з'являється в результаті досвіду;
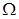- простір елементарних подій;
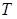- область (безліч) значень аргументу t функції X(t);
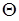- безліч можливих значень випадкового процесу X(t).
Припустимо, що дослід, в ході якого випадковий процес протікає, вже зроблений, тобто відбулося елементарна подія 
. Це означає, що випадковий процес вже не випадковий, і залежність його від прийняла цілком певний вид.
Це вже звичайна, невипадкова функція аргументу t. Ми будемо її називати реалізацією випадкового процесу X(t) в даному досвіді.
Реалізацією випадкового процесу X(t) називається невипадкова функція X(t), на яку перетворюється випадковий процес X(t) в результаті досвіду. Реалізацію випадкового процесу як функцію 
від аргументу t, що змінюється в межах безлічі T, при фіксованому елементарному подію 
, записують так:
; 
; 
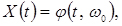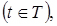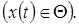(4.2)
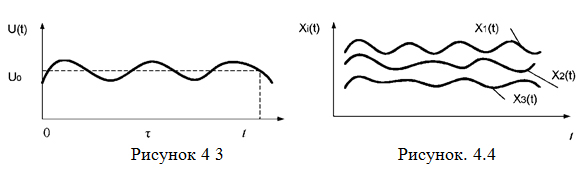
Приклад. Записуючи за допомогою приладу напруга U живлення ЕОМ залежно від часу t на ділянці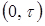 
, отримаємо реалізацію та u(t) випадкового процесу U(t), де u0 - номінальна напруга живлення (рис. 4.3).
Якщо проведений не один дослід, а декілька, в результаті кожного з яких спостерігається якась реалізація випадкового процесу xi(t) (I - номер досвіду, тому отримаємо кілька різних реалізацій випадкового процесу: x1(t), x2(t), ..., xn(t) або сімейство реалізацій) (рис. 4.4).
Сімейство реалізацій випадкового процесу - основний експериментальний матеріал, на основі якого можна отримати характеристики випадкового процесу.
Випадкові процеси класифікуються «за часом» і «по станам» системи.
Випадковий процес X(t) називається процесом з дискретним часом, якщо система, в якій він протікає, може міняти свій стан тільки в моменти t1, t2, …, tn число яких звичайно.
Випадковий процес X(t) називається процесом з безперервним часом, якщо переходи системи з одного стану в інший можуть відбуватися в будь-який момент часу t спостережуваного періоду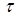 
.
Випадковий процес X(t) називається процесом з безперервним станом, якщо його течія в будь-який момент t являє собою безперервну випадкову величину і безлічі її значень 
незліченно.
Випадковий процес X(t) називається процесом з дискретним станом, якщо в будь-який момент часу t безліч його станів 
звичайно або лічильно.
4.1.1 Характеристики випадкових процесів
Основними характеристиками випадкових процесів є: математичне сподівання, дисперсія, коваріація, початковий і центральні моменти різних порядків і т.д.
Математичне сподівання випадкового процесу X(t) називається невипадкова функція mx(t), яка при будь-якому значенні аргументу t дорівнює математичному очікуванню відповідного перетину випадкового процесу.
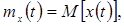(4.3)
де mx(t) - середня функція (рис. 4.5).
Рисунок 4.5 – Математичне сподівання випадкового процесу X(t)
Приклад. Якщо перетин випадкового процесу X(t) при даному t являє дискретну випадкову величину з низкою розподілу X(t)
Таблиця 4.1 – Випадковий процес
x1(t) |
x2(t) |
x3(t) |
... |
xi(t) |
... |
p1(t) |
p2(t) |
p3(t) |
... |
pi(t) |
... |
то його математичне сподівання обчислюється за формулою
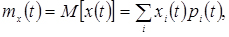(4.4)
де x1(t) , x2(t) і т.д. - перше, друге і т.д. значення, які може приймати випадкова величина;
X(t)- перетин випадкового процесу при даному t;
p1(t), p2(t) і т. д. - відповідні ймовірності.
Якщо перетин випадкового процесу X(t) при даному t являє собою безперервну випадкову величину з щільністю f(t,x), то його математичне сподівання може бути обчислено за формулою
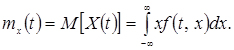(4.5)
Центровані випадковим процесом X(t) називається процес, який виходить, якщо з випадкового процесу X(t) вирахувати його математичне сподівання
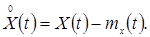(4.6)
Початковим моментом k-го порядку випадкового процесу X(t) називається математичне сподівання k-го ступеня відповідного перетину випадкового процесу
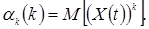(4.7)
Центральний момент k-го порядку - математичне сподівання k-го ступеня центрованого випадкового процесу
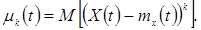(4.8)
Дисперсія випадкового процесу
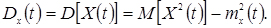(4.9)
Дисперсією випадкового процесу X(t) називається невипадкова функція Dx(t), яка при будь-якому значенні аргументу t дорівнює дисперсії відповідного перетину випадкового процесу X(t).
Якщо перетин X(t) являє собою дискретну випадкову величину з низкою розподілу X(t)
Таблиця 4.1 – Випадковий процес
x1 |
x2 |
... |
xi |
... |
p1(t) |
p2(t) |
... |
pi(t) |
... |
то дисперсія випадкового процесу знаходиться за формулою
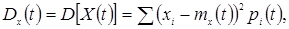(4.10)
де i - номер можливого значення випадкової величини X(t) при даному t; pi(t) - ймовірність цього значення.
Якщо перетин X(t) являє собою безперервну випадкову величину з щільністю f(t,x), то дисперсія випадкового процесу може бути обчислена за формулою
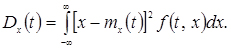(4.11)
Середнім квадратичним відхиленням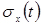 
випадкового процесу X(t) називається арифметичне значення кореня квадратного з дисперсії Dx(t)
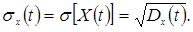(4.12)
Ступінь залежності (зв'язку) між двома випадковими величинами Х і У визначається їх коваріацією
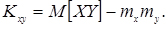(4.13)
Аналогічна характеристика вводиться і для випадкового процесу.
Розглянемо дві випадкових величини – два перетина випадкового процесу для моментів t і t' (див. рис. 4.6.): X(t) і X(t') . Для цих двох випадкових величин можна знайти коваріацію (позначимо її Kx(t,t')):
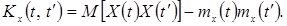(4.14)
Остання функція називається кореляційною функцією випадкового процесу.
Отже, кореляційна функція випадкового процесу X(t) - називається невипадкова функція Kx(t,t') двох аргументів t і t' яка при кожній парі значень аргументів t і t' дорівнює коваріації відповідних перерізів випадкового процесу: X(t) і X(t'). На рис. 4.7 показаний вигляд поверхні, яка зображує кореляційну функцію Kx(t,t'). Поверхня Kx(t,t') симетрична щодо вертикальної площини Н, що проходить через бісектрису координатного кута t 0 t'.
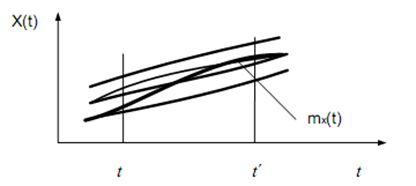
Рисунок 4.6 – Два перетина випадкового процесу для моментів t і t'
Лінія перетину площини Н з поверхнею Kx(t,t') дає аплікат рівну дисперсії випадкового процесу X(t)
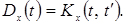(4.15)
Нормованою кореляційною функцією rx(t,t') випадкового процесу X(t) називається функція, отримана діленням кореляційної функції Kx(t,t') на “произведение” середніх квадратичних відхилень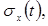 
, 
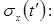
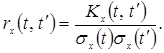(4.16)
Нормована кореляційна функція за модулем не перевищує одиницю:
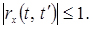(4.17)
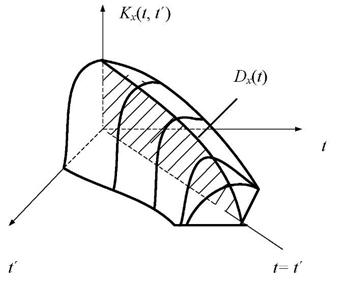
Рисунок 4.7 – Вигляд поверхні, яка зображує функцію Kx(t,t')
4.1.2 Закони розподілу випадкових процесів
Для різних типів випадкових процесів розроблені різні методи їх вивчення та опису. У ряді завдань випадкові процеси буває зручно виражати через найпростіші (елементарні) випадкові функції.
Елементарною випадковою функцією (ЕВФ) називають таку функцію аргументу t представлена звичайною, невипадковою функцією, в яку входять одна або кілька звичайних параметрів, не залежних від t випадкових величин.
Приклад 1. ЕВФ має вигляд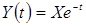 
, де X - неперервна випадкова величина, розподілена рівномірно в інтервалі (-1, 1).
Сімейство реалізації ЕВФ Y(t) показано на рис. 4.8. Кожна з них являє собою показову криву з ординатами, пропорційними ординатам кривої e-t (жирна лінія); окремі реалізації (тонкі лінії) розрізняються між собою масштабом по осі ординат. Коли випадкова величина X приймає негативне значення, відповідна реалізація лежить нижче осі абсцис.
Приклад 2. ЕВФ має вигляд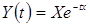 
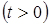, де X - випадкова величина, що приймає тільки позитивні значення. Yi(t) - i-я реалізація, що представляє собою показову криву, що проходить через точку з координатами (0, 1), розрізняються вони між собою швидкістю прагнення до нуля або 
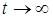(рис. 4.9.).
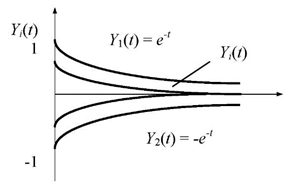
Рисунок 4.8 – Сімейство реалізації ЕВФ Y(t)
Приклад 3. ЕВФ має вигляд Y(t)=at+X, де X- випадкові величини, a- невипадкова величина. Кожна реалізація (рис. 4.10) являє собою пряму з кутовим коефіцієнтом a, паралельну пряму y=at, відрізняються реалізації початковими ординатами.
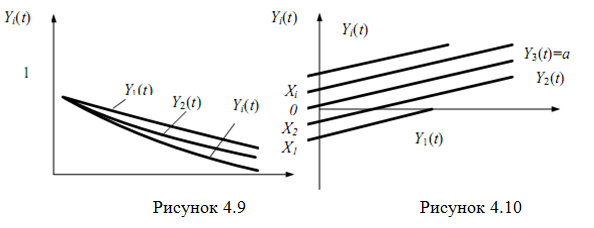
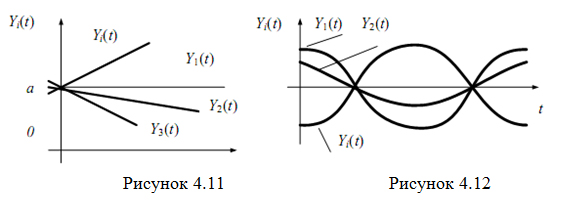
Приклад 4. Y(t)=Xt+a, де X- випадкова величина, a- невипадкова величина. Кожна з реалізацій - пряма лінія, що проходить через точку (0, a) (рис. 4.11). Реалізації розрізняються кутовими коефіцієнтами.
Приклад 5. ЕВФ має вигляд Y(t)= X cos(at),
де X - випадкова величина, a - невипадкова величина. Сімейство реалізацій показано на рис. 4.12; кожна з них - косінусоіда, ординати якої помножені на той чи інший випадковий коефіцієнт. Реалізації різняться між собою амплітудою, тобто масштабом по осі ординат.
Відомо, що універсальною вичерпною характеристикою будь-якої випадкової величини є її функція розподілу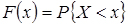 
, тобто ймовірність того, що випадкова величина X приймає значення, менше заданого x. Нехай маємо випадковий процес X(t). Будь-який перетин випадкового процесу X(t) являє собою випадкову величину, яка має закон розподілу
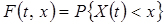
Ця функція залежить від двох аргументів: по-перше, від значення t, для якого береться розтин; по-друге, від значення x, менше якого повинна бути випадкова величина X(t). Вона називається одновимірним законом розподілу випадкового процесу X(t). Очевидно, одновимірний закон розподілу не може служити повною вичерпною характеристикою випадкового процесу X(t). Більш повною характеристикою буде двомірний закон розподілу, представлений спільною функцією розподілу двох перерізів випадкового процесу, взятих відповідно для моментів t1 і t2:
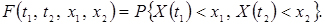
Ця функція вже не двох, а чотирьох аргументів. Очевидно, теоретично можна необмежено збільшувати число значень і отримати при цьому все більш повну характеристику випадкового процесу. Однак оперувати з настільки громіздкими характеристиками, що залежать від багатьох аргументів, вкрай незручно. В інженерних додатках зазвичай обмежуються одномірним, іноді - двомірним законом розподілу випадкового процесу.
4.2 Марківські випадкові процеси
Розглянемо фізичну систему S, в якій протікає випадковий процес з дискретними станами:S1, S2,...,Si,...,Sn, число яких звичайно. При цьому під системою S будемо розуміти технологічний пристрій (автомобіль, ремонтна майстерня, СТОА, АЗС і т.д.).
Процес з дискретними станами характеризується тим, що система S стрибками час від часу переходить з одного стану (Si) в інше (Sj).
При вивченні таких процесів кожний стан прийнято зображати у вигляді прямокутника або кружка, а можливі переходи зі стану в стан - стрілками, що з'єднують ці прямокутники. Отриману схему називають графіком станів.
Приклад. Система S - автомобіль, може знаходитися в одному з п'яти можливих станів (рис.4.20). S1 - справний, працює; S2 - несправний, очікує ремонту; S3- оглядається; S4- ремонтується; S6- списаний.
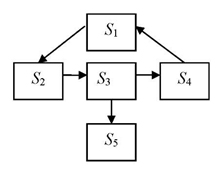
Рисунок 4.13 – Граф станів системи
При аналізі випадкових процесів, що протікали в системах з дискретними станами, важливу роль відіграють ймовірності станів.
Позначимо S(t) стан системи S у момент t. Ймовірність i-го стану в момент t називається ймовірність події, що складається в тому, що момент t система буде в змозі Si; позначимо її pi(t):
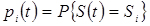(4.18)
де S(t) - випадковий стан системи в момент t.
Очевидно, що для системи з дискретними станами S1, S2,..., Si, у будь-який момент часу t сума ймовірностей станів дорівнює одиниці
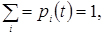(4.19)
як сума ймовірностей повної групи незалежних подій.
Зазначимо, що випадковий процес, що протікає в системі S з дискретними станами S1, S2,..., Si, називається Марківським, якщо для будь-якого моменту часу t ймовірність кожного з станів системи в майбутньому (при t>t0) залежить тільки від її стану в сьогоденні (при t=t0) і не залежить від того, коли і як вона прийшла в цей стан, тобто не залежить від її появи в минулому (при t
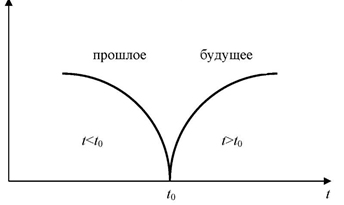
Рисунок 4.14 – Випадковий процес
4.3 Методи теорії масового обслуговування
Теорія масового обслуговування (queueing theory) описує процеси, що протікають в системах масового обслуговування (СМО) (рис. 4.15). До СМО відносяться ремонтні майстерні, станції технічного обслуговування, автозаправні станції тощо.
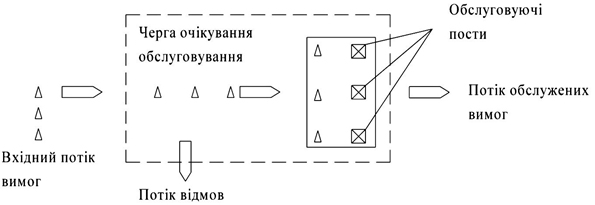
Рисунок 4.15 – Система масового обслуговування
Випадковий характер потоку заявок призводить до того, що в СМО відбувається якийсь випадковий процес. Якщо випадковий процес Марківський, то функціонування СМО можна описати системою диференціальних рівнянь, а в граничному випадку - системою лінійних алгебраїчних рівнянь, рішенням яких визначаються характеристики роботи СМО.
Методи теорії масового обслуговування дозволяють вирішувати наступні завдання автомобільного транспорту:
- визначити кількість ліній або постів ТО і Р автомобілів;
- визначити раціональне кількість оборотних агрегатів;
- проводити розрахунок кількості постів навантаження і розвантаження автомобілів, а також багато інших завдань.
При аналізі роботи СМО необхідно знати її основні вихідні параметри:
- інтенсивність потоку заявок -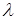 
;
- трудомісткість обслуговування однієї заявки - Тр;
- число каналів обслуговування - n;
- число місць очікування - m;
- кількість операторів на кожному каналі - d;
- умови, що накладаються на освіту черги.
При описі режиму роботи СМО використовуються проміжні параметри:
- час обслуговування однієї заявки - T0=Tp/d;
- продуктивність кожного каналу обслуговування -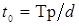 
; (середнє число заявок, яке обслуговується каналом в одиницю часу);
- приведена інтенсивність обслуговування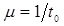 
;
- коефіцієнт завантаження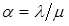 
.
4.3.1 Показники роботи систем масового обслуговування
Системи масового обслуговування поділяються по ряду ознак:
1. За часом очікування (Tx):
- без очікування або з втратами вимог (Tx=0);
- з очікуванням або без втрат (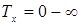
);
- з обмеженим часом очікування (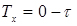
).
Системи з необмеженим очікуванням початку технічного впливу є найбільш реальним. Це обумовлено тим, що в умовах України перегони (нульові пробіги) до поста обслуговування досить великі. Існує дефіцит запчастин і матеріалів, відсутня оперативний зв'язок між регіональними СТОА, не розвинені фірмові системи сервісу і т.п. Тому клієнт змушений чекати початку обслуговування іноді і поза зони очікування.
2. За кількістю вимог на добу (Nc):
- з обмеженим вхідним потоком, або замкнуті (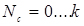
);
- з необмеженим потоком, або відкриті (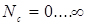
).
Число вимог на СТОА не може бути заздалегідь обмежена, системи є відкритими (розімкненими).
3. За кількістю каналів (обслуговуючих апаратів):
- з обмеженим числом обслуговуючих апаратів (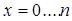
);
- з необмеженим числом обслуговуючих апаратів (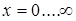
).
4. За кількістю фаз (r):
- однофазні (r=1);
- багатофазні (r>1).
Багатофазні СМО використовуються при потоковому вигляді обслуговування (наприклад, діагностика - ТО).
5. За рівнем організації:
- упорядковані (ентропія E=1);
- невпорядковані (E > 1).
Порядок обслуговування встановлюється в результаті аналізу СМО.
При подальшому розгляді питань функціонування СМО ми зупинимося на двох основних видах: СМО з відмовами; СМО з очікуванням обслуговування.
У системах з відмовами обслуговуються тільки ті вимоги, які надходять в момент часу, коли хоча б один з каналів обслуговування був вільний. Якщо всі канали зайняті, то заявка покидає СМО не обслуженою.
У СМО з очікуванням заявка, що надійшла в момент, коли всі канали зайняті, чекає звільнення каналу обслуговування, тобто стає в чергу.
Розрізняють одноканальні і багатоканальні СМО з очікуванням, при цьому на довжину черги можуть бути накладені обмеження, що визначають максимальну довжину черги.
Всі показники (характеристики) функціонування СМО можна розділити на чотири групи: імовірнісні; кількісні; тимчасові; якісні.
Імовірнісні показники. Будемо говорити, що вимога знаходиться в СМО, якщо вона очікує обслуговування або знаходиться на обслуговуванні. Позначимо J число вимог, що знаходяться в СМО. Так як з плином часу це число змінюється, то J є випадковою величиною. Припустимо, що вироблено дуже велика кількість спостережень над СМО, в результаті яких встановлено частку випадків, коли в системі спостерігалося рівно J вимог. Ця величина називається ймовірністю pJ того, що в СМО мається J вимог.
Всі ймовірності станів повинні задовольняти умови нормування, згідно з яким сума всіх ймовірностей повинна дорівнювати одиниці, тобто
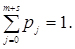(4.20)
Вимога отримує відмову в тому і тільки в тому випадку, якщо в момент свого вступу до СМО застає зайнятими як всі канали, так і всі місця накопичення. Якщо в системі є п апаратів і т місць накопичувача, то ймовірність даної події дорівнює
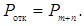(4.21)
Ця ймовірність називається ймовірністю відмови.
Імовірність знаходження в СМО не більше i вимог
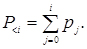(4.22)
Імовірність відсутності черги
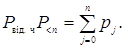(4.23)
Ймовірність того, що вимогу не доведеться чекати початку обслуговування
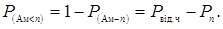(4.24)
Імовірність наявності черги
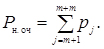(4.25)
Ймовірність того, що всі обслуговуючі апарати зайняті
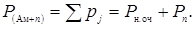(4.26)
Ймовірність обслуговування
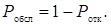(4.27)
Кількісні показники.
Середнє число вільних обслуговуючих апаратів
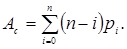(4.28)
Середнє число вимог зайнятих обслуговуючих апаратів
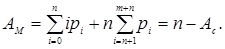(4.29)
Середнє число вимог у накопичувачі
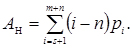(4.30)
Середнє число вимог в обслуговуючій системі
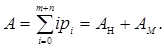(4.31)
Середнє число вимог, які отримують відмову за одиницю часу
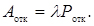(4.32)
Тимчасові показники. Важливим показником є середній час очікування початку обслуговування Tоч. Сума середнього часу очікування Tоч і обслуговування Tобсл дорівнює середньому часу перебування вимоги в системі
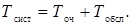(4.33)
Встановимо корисний зв'язок між середнім числом вимог, що знаходиться в системі, і середнім часом перебування вимоги в системі. Так як за одиницю часу в систему надходить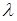 
вимог, а середня тривалість перебування однієї вимоги в системі є Tсист, то сумарна тривалість знаходження всіх вимог у системі за одиницю часу дорівнює (
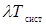). Але так як в системі знаходиться в середньому А вимог, то ця величина дорівнює добутку одиниці часу на А, тобто
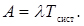(4.34)
Аналогічно можна вивести формулу
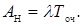(4.35)
Якісні показники. Наведені показники характеризують ступінь використання обслуговуючих апаратів і витрати часу на перебування вимог у системі (у черзі і на обслуговування). Зазвичай буває необхідним узгодити ці величини, щоб знайти економічно оптимальне рішення. У зв'язку з цим припустимо, що за одиницю часу перебування вимоги в системі обслуговування мають місце збитки, рівні С. Крім того, експлуатація одного апарату призводить за одиницю часу до витрат, рівним К. Відзначимо, що у величину К звичайно входять як експлуатаційні витрати, так і питомі капітальні витрати на один апарат, пов'язані з його придбанням і припадають на одиницю часу. Нехай далі відмова в обслуговуванні однієї вимоги тягне збиток, рівний C0.
Тоді наведені середні витрати, пов'язані з експлуатацією п апаратів, надходженням в систему в одиницю часу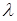 
вимог і збитками від відмов вимогам, в одиницю часу в середньому становлять
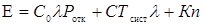(4.36)
У цьому виразі Tсист (середній час перебування однієї вимоги в системі), а разом з ним і доданок (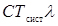
) зменшуються із зростанням числа обслуговуючих апаратів п. На противагу цьому доданок Кп із зростанням числа апаратів збільшується. Завдання полягає, отже, у виборі такого значення п, при якому критерій (Е) буде мінімальний. Такий вибір п забезпечує мінімізацію наведених витрат, пов'язаних з придбанням та експлуатацією апаратів і непродуктивним перебуванням вимог у системі обслуговування.
Відзначимо також, що за рахунок додаткових витрат часто є можливість зменшити середню тривалість обслуговування однієї вимоги Tобсл. При цьому буде зменшуватися і величина Tсист- середній час перебування вимоги в системі. У цьому випадку для знаходження оптимального рішення в критерій Е слід ввести також зазначені додаткові витрати.
Наступним показником якості функціонування СМО є:
- коефіцієнт завантаження поста:
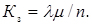(4.37)
- коефіцієнт використання апаратів
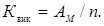(4.38)
4.3.2 Характеристики систем масового обслуговування
1. Системи масового обслуговування з відмовами.
Нехай маємо п-канальну СМО з відмовами, в яку надходить потік вимог (автомобілів) на обслуговування з інтенсивністю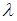 
, інтенсивність обслуговування одного каналу дорівнює 
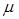. Визначимо показники ефективності роботи такої системи, для чого побудуємо розмічений граф станів системи (рис. 4.27), де стани системи пронумеровані за кількістю зайнятих каналів, тобто
S0 - всі канали вільні;
S1 - зайнятий один канал, решта вільні;
S2 - зайняті два канали, решта вільні;
……………………………………....
Sn - зайняті всі п каналів.
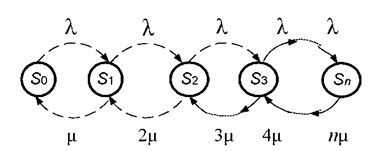
Рисунок 4.27 – Розмічений граф станів
За стрілкою зліва направо систему переводить потік заявок з інтенсивністю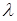 
. По стрілках справа наліво систему переводить потік обслуговувань інтенсивністю 
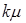, де k - число зайнятих каналів.
Для обчислень граничних ймовірностей станів системи (Pi) запишемо систему лінійних рівнянь. Згідно рис. 27 будемо мати:
Таблиця 4.1
k |
Рівняння |
Ймовірність стану системи |
1 |
2 |
3 |
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
Продовження таблиці 4.1
1 |
2 |
3 |
…. |
………………… |
………………… |
k |
|
|
…. |
………………… |
………………… |
n |
|
|
Рекурентний вираз для визначення ймовірності стану дорівнюватиме
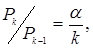(4.39)
де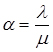 
.
Запишемо нормувальну умову:
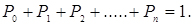(4.40)
Вирішуючи його спільно з системою рівнянь табл. 4.1, отримаємо:
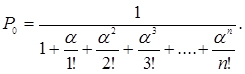
Решта ймовірності станів знайдемо з виразів табл. 4.1.
Знаючи граничні ймовірності станів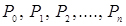 
, обчислимо характеристики роботи СМО.
Імовірнісні характеристики:
- ймовірність того, що всі канали зайняті і відмова в обслуговуванні
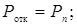(4.41)
- відносна пропускна здатність
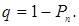(4.42)
Кількісні характеристики:
- середня кількість зайнятих постів
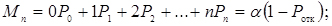(4.43)
- середня кількість каналів, вільних від обслуговування
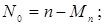(4.44)
- абсолютна пропускна здатність
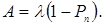(4.45)
Тимчасові характеристики:
- середній час обслуговування
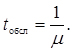(4.46)
Якісні характеристики:
- коефіцієнт зайнятості каналів
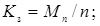(4.47)
- коефіцієнт простою каналів
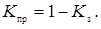(4.48)
Системи масового обслуговування з очікуванням.
1. Одноканальна СМО з очікуванням
Нехай СМО має один канал, на який надходить потік заявок з інтенсивністю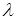 
. Інтенсивність обслуговування каналу дорівнює 
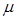. Заявка, що надійшла в момент, коли канал зайнятий, стає в чергу і чекає обслуговування. Припустимо, що число місць у черзі рівне m, тобто, якщо заявка, що прийшла в момент, коли в черзі стоїть m заявок, покидає СМО не обслуженою.
Будемо нумерувати стану СМО за кількістю заявок, що знаходяться в системі (як обслуговуються, так і очікують обслуговування):
S0- канал вільний;
S1- канал зайнятий, черги немає;
S2- канал зайнятий, одна заявка в черзі;
…………………………………………….
Sn- канал зайнятий, заявок в черзі.
Складемо розмічений граф станів системи (рис. 4.28)
Система диференціальних рівнянь Колмогорова для даного процесу має вигляд:
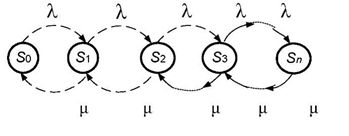
Рисунок 4.28 – Розмічений граф стану
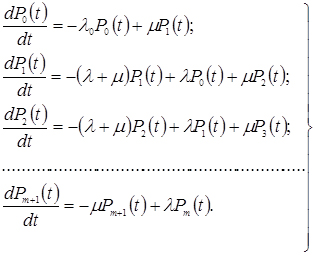(4.49)
Додамо до цієї системи початкові умови. Наприклад, якщо при t=0 система перебуває в стані S0, то початкові умови приймуть вигляд:
; 
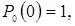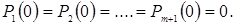(4.50)
Проінтегрувавши систему (1) при прийнятих початкових умовах, отримаємо всі ймовірності стану як функції часу
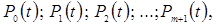(4.51)
які в будь-який момент часу t задовольняють умову
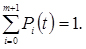(4.52)
Якщо в системі диференціальних рівнянь (4.49) покласти всі похідні рівні нулю (при залежність від часу пропадає), то вона перетворюється на систему звичайних лінійних алгебраїчних рівнянь, яка спільно з нормованою умовою (4.52) дає можливість обчислити всі граничні ймовірності станів.
При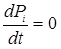 
маємо
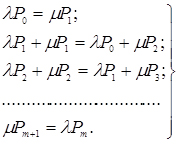(4.53)
Після перетворень система (4.53) перепишеться у вигляді рівнянь (табл. 4.2).
Таблиця 4.2 – Формули для визначення решти ймовірності станів
1 |
|
2 |
|
3 |
|
… |
|
m+1 |
|
Остаточний вираз для P0 має вигляд
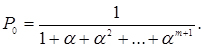(4.54)
Решта ймовірності станів можна знайти за формулами в табл.4.2.
Багатоканальна СМО з очікуваннями.
Нехай маємо п-канальну СМО з очікуванням, на яку надходить потік заявок з інтенсивністю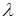 
, інтенсивність обслуговування одного каналу дорівнює 
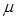, число місць у черзі обмежено заданим числом m. Обчислити основні характеристики СМО.
Стан системи будемо нумерувати за кількістю заявок, пов'язаних з системою:
S0- всі канали вільні;
S1- зайнятий тільки один канал;
S2- зайняті тільки два канали;
Sn- зайняті всі п канали.
Коли СМО знаходиться в будь-якому з цих станів, черги ще немає. Після того, як будуть зайняті всі канали обслуговування, а заявки продовжують надходити, утворюється черга. Тоді стану системи будуть:
Sn+1- зайняті всі n каналів і одна заявка в черзі;
Sn+2- зайняті всі n каналів і дві заявки в черзі;
…………………………………………………..
Sn+m- зайняті всі n каналів і всі m місць у черзі.
Граф станів системи представлений на рис. 4.29.
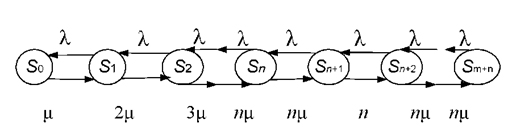
Рисунок 4.29 – Розмічений граф стану
Дійсно, перехід системи в стан з великими номерами (зліва направо) викликається тільки потоком заявок з інтенсивністю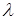 
. По стрілках справа наліво систему переводить потік обслуговування, інтенсивність якого дорівнює 
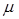, помножена на число зайнятих каналів. Дійсно, повна інтенсивність потоку обслуговування зростає з підключенням нових каналів аж до такого стану 
, коли всі п канали позначаться зайнятими. З появою черги інтенсивність обслуговування більше не збільшується, оскільки вона вже досягла максимуму, рівного (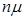
).
Не повторюючи відповідних міркувань, запишемо відразу в остаточному вигляді основні формули, що відображають роботу СМО з очікуванням, ввівши для спрощення запису позначення
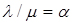- приведена інтенсивність; 
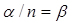- навантаження.
Таблиця 4.3 – До виникнення черги
k |
Рівняння |
Ймовірність стану системи |
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
…. |
………………… |
………………… |
k |
|
|
…. |
………………… |
………………… |
n |
|
|
Таблиця 4.4 – Після виникнення черги
k |
Рівняння |
Ймовірність стану системи |
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
…. |
………………… |
………………… |
l |
|
|
…. |
………………… |
………………… |
m |
|
|
Обчислимо основні характеристики СМО, для чого запишемо нормувальну умову
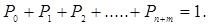(4.55)
і підставимо в нього значення ймовірностей Pi(виражені через ймовірність P0, тоді ймовірність того, що всі канали вільні - визначається за виразом
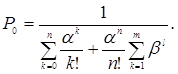(4.56)
Інші ймовірності станів визначаються за даними табл. 4.3.
Ймовірність того, що всі канали і місця очікування зайняті і заявка отримує відмову в обслуговуванні
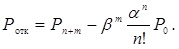(4.57)
Відносна пропускна здатність
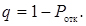(4.58)
Середнє число каналів, зайнятих обслуговуванням
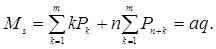(4.59)
Середнє число каналів, вільних від обслуговування
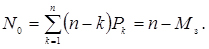(4.60)
Середнє число заявок у накопичувачі
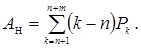(4.61)
Абсолютна пропускна здатність
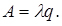(4.62)
Середній час очікування обслуговування заявки в черзі
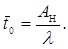(4.63)
Середній час перебування заявки в системі
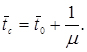(4.64)
Коефіцієнт зайнятості каналів
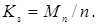(4.65)
Коефіцієнт простою каналів
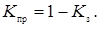(4.66)
4.4 Оптимізація числа оборотних агрегатів методами теорії масо-вого обслуговування
Раціональне управління виробництвом і розподілом оборотного фонду запасних частин, вузлів і агрегатів, що використовуються при ремонті автомобілів, має важливе виробниче значення.
Одним з методів вирішення поставленого завдання може служити математичний апарат теорії масового обслуговування, що описує процеси, які протікають в СМО.
У системах масового обслуговування потік вимог є випадковим. Випадково і час обслуговування.
Робота СМО протікає нерегулярно; то утвориться черга на обслуговування, то відбувається простій постів (апаратів) обслуговування. Завдання теорії масового обслуговування - встановити оптимальну (з мінімальними простоями) залежність між характером потоку вимог, числом постів та їх продуктивністю (часом обслуговування), правилами роботи системи обслуговування.
Найбільш часто в якості критеріїв – показників ефективності роботи систем масового обслуговування – використовуються показники середнього часу очікування вимоги початку обслуговування; середнього розміру черги на обслуговування; ймовірності того, що в системі обслуговування перебуватиме певна кількість вимог; середнє число апаратів, зайнятих або вільних від обслуговування, і ряд інших. Однак найбільш доцільно використовувати економічні показники оцінки ефективності функціонування систем масового обслуговування, які дають узагальнену характеристику виробничого процесу. У цьому випадку в якості критерію ефективності функціонування СМО зазвичай вибираються загальні грошові витрати, пов'язані з простоями автомобілів в очікуванні обслуговування, і витрати на створення та експлуатацію постів (апаратів).
Приклад. У автотранспортному підприємстві, що має одномарочний рухомий склад, застосовується агрегатний метод ремонту. Ремонт здійснюється шляхом заміни несправного агрегату на придатний, взятий зі складу. За відсутності на складі агрегатів автомобіль очікує ремонту.
У даному прикладі вхідний потік вимог утворюють автомобілі з несправними агрегатами. Обслуговуючими апаратами є оборотні агрегати. Дисципліна заміни агрегатів - у порядку надходження вимог, а процес заміни їх можна розглядати як СМО з очікуванням.
Задачу оптимізації оборотного фонду агрегатів автотранспортного підприємства зведемо до відшукання мінімуму цільової функції
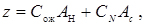(4.67)
де Cож - витрати в гривнях, що викликаються простоєм одного автомобіля в очікуванні надходження відремонтованого агрегату протягом доби;
AH- середня кількість несправних автомобілів, які очікують надходження відремонтованих агрегатів (середнє число автомобілів);
CN- витрати, викликані невикористанням одного відремонтованого агрегату протягом доби;
Ac- середня кількість невикористаних агрегатів (пролежали на складі).
Cож і CN визначаються шляхом калькуляції. AH і Ac визначаються методами теорії масового обслуговування для конкретних умов виробничої діяльності АТП і залежать від числа оборотних агрегатів N.
Якщо автомобілі надходять на ремонт (заміну агрегату) з інтенсивністю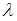 
, а середній час повернення агрегату на склад становить 
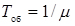, то для розімкнутої системи масового обслуговування з очікуванням маємо такі розрахункові формули.
Для спрощення формул використовуються вирази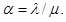 
Завантаження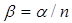 
.
Ймовірність того, що всі обслуговуючі апарати (агрегати) вільні
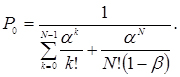(4.68)
Ймовірність того, що всі обслуговуючі апарати (агрегати) зайняті
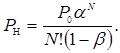(4.69)
Середнє число вимог (автомобілів) у накопичувачі
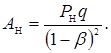(4.70)
Середнє число вільних обслуговуючих апаратів(агрегатів)
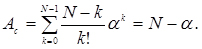(4.71)
Первісна розрахункова кількість оборотних агрегатів визначається за умовою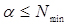 
. Зміною числа оборотних агрегатів від Nmin до N (рис. 30) визначимо оптимальне число оборотних агрегатів з умови цільової функції 
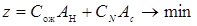. Розрахунок параметрів функціонування подібних систем масового обслуговування доцільно здійснювати на ЕОМ.
Результати розрахунків за наведеною програмою для одного варіанта вихідних даних можуть мати вигляд: вихідні дані L=1; T1=3; Cож=25; CN=3 приведена інтенсивність А = 3; N = 8, N - кількість каналів (агрегатів) обслуговування; Z - витрати сумарні, грн. Авт. - середня кількість несправних автомобілів в накопичувачі; Агр. - середня кількість невикористаних агрегатів; V - зміна сумарних витрат, грн.
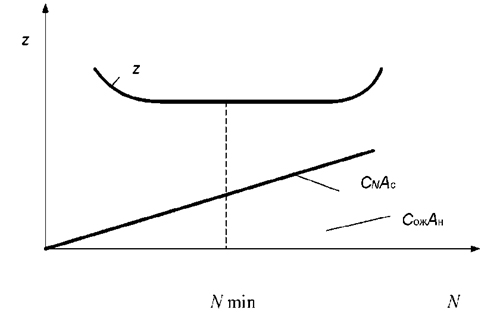
Рисунок 4.30 – Графік витрат у системі масового обслуговування
Контрольні запитання
1. Дайте визначення таким поняттям: випадковий процес; реалізація випадкового процесу; перетин випадкового процесу.
2. Наведіть класифікацію випадкових процесів.
3. Перерахуйте основні характеристики випадкових процесів.
4. Дайте визначення потоку подій, назвіть ознаки, за якими вони поділяються.
5. Перерахуйте властивості найпростішого потоку подій.
6. Що таке інтенсивність потоку подій? Фізичний зміст інтенсивності потоку подій.
7. Особливості потоку Пальма і Ерланга.
8. Дайте визначення Марковському випадковому процесу.
9. Назвіть основні характеристики випадкового процесу з дискретними станами і дискретним часом.
10. Правила запису рівнянь Колмогорова.
11. Дайте визначення граничним ймовірностям станів.
12. Зобразіть графічно випадковий процес чистого «розмноження» і процес чистої «загибелі».
13. Перерахуйте ознаки, за якими поділяються СМО.
14. Назвіть основні вихідні параметри, які використовуються при аналізі роботи СМО.
15. Запишіть основні імовірнісні показники функціонування СМО.
16. Зобразіть розмічений граф станів багатоканальної СМО з очікуванням.
17. Запишіть формули підрахунку середнього числа зайнятих каналів і середнього числа заявок, що стоять в черзі.
