5 СТАТИСТИЧНЕ ІМІТАЦІЙНЕ МОДЕЛЮВАННЯ
Основною перевагою імітаційних моделей (simulation model) в порів-нянні з аналітичними є можливість вирішувати завдання виняткової складності з урахуванням випадкових чинників.
Метод імітаційного моделювання вдається успішно реалізувати за допомогою ЕОМ. Проте використання ЕОМ для цілей імітаційного моделювання вимагає вміння розробки моделюючого алгоритму, який повинен відтворити формальний процес складної системи. Моделюючий алгоритм дозволяє за вихідними даними отримати відомості про стани виробничого процесу в довільний момент часу.
Розробка моделюючого алгоритму неможливо без глибокого знання модельованого об'єкта і його функціонування, причому, в процесі розробки відбувається поглиблення та уточнення розуміння об'єкта. Тому процес розробки моделі має і самостійне значення. Оскільки дозволяє виявити недоліки, розкрити резерви, відкрити нові можливості об'єкта ще до моделювання і дати важливі практичні рекомендації щодо вдосконалення об'єкту і підвищенню ефективності його функціонування.
Однією з переваг моделювання виробничих процесів є можливість розгляду змінних факторів у всьому діапазоні їх значень.
Імітаційне моделювання, при якому відтворюються випадкові явища, називається статистичним імітаційним моделюванням. Статистичне іміта-ційне моделювання базується на чисельному статистичному методі вирі-шення математичних завдань, який називається методом Монте-Карло.
5.1 Загальні положення
Метод статистичного моделювання зазвичай включає наступні етапи:
1. Спочатку дається опис функціонування системи, тобто опис завдань, що стоять перед системою, уточнюються вихідні (відправні) положення; розглядаються обмеження; виділяються підпроцеси; намічаються характеристики, які потрібно отримати на виході, і вибирається цільова функція або критерій, за допомогою якого буде проводитися оцінка ефективності функціонування системи.
2. Проводиться збір та обробка інформації, що характеризує роботу підпроцесів системи і всього процесу в цілому.
3. Виконується формалізація роботи системи, тобто виділяються головні фактори і виключаються другорядні, якими можна знехтувати. На основі цього складається відповідальна система адекватна математична модель процесу.
4. Складається алгоритм прийнятої математичної моделі у вигляді операторної блок - схеми.
5. Складається програма для багаторазового відтворення на ЕОМ процесі при числі реалізацій, що забезпечують задану точність.
6. Виконується моделювання роботи системи на ЕОМ і видача на друк основних результатів моделювання. Зазвичай при цьому отримують:
а) точкові оцінки, тобто математичне сподівання, дисперсію для кожного з підпроцесів і по всьому процесу в цілому;
б) інтервальні оцінки, тобто довірчі інтервали та довірчі смуги розкиду середнього результату для кожного з підпроцесів і всього процесу в цілому;
в) будуються криві рівнянь регресії, що характеризують залежність досліджуваних параметрів від різних аргументів.
Крім перерахованого, можуть обчислюватися спеціальні характеристики, властиві розглянутого явища. Все це дозволяє прогнозувати перебіг процесу і введенням відповідних поправок оптимізувати його перебіг.
Якщо випадковий процес, що протікає в системі, відбувається під дією довільного потоку подій, то його математичну модель побудувати важко. У цьому випадку можна використовувати метод статистичного моделювання (метод Монте-Карло), який заснований на законі великих чисел.
У загальному вигляді закон великих чисел (теорема Чебишева П.Л.) записується так^
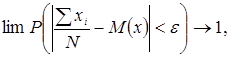 (5.1)
(5.1)
де Р - ймовірність складної події;
![]() – математичне сподівання випадкової величини;
– математичне сподівання випадкової величини;
![]() – середнє арифметичне спостережуваних значень;
– середнє арифметичне спостережуваних значень;
N – число випробувань (число реалізацій);
![]() – як завгодно мале позитивне число.
– як завгодно мале позитивне число.
Теорема Чебишева формулюється так: «При великому числі випробувань середнє арифметичне спостережуваних значень випадкової величини сходиться по ймовірності до її математичного сподівання».
При переході до відносних (без розмірності) параметрам, маємо окремий випадок закону великих чисел (теорема Я. Бернуллі), який аналітично записується так:
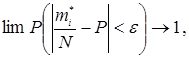 (5.2)
(5.2)
де ![]() – число появи події (частота);
– число появи події (частота);
![]() – частость події;
– частость події;
![]() – ймовірність події.
– ймовірність події.
Теорема Я. Бернуллі формулюється так: «При великому числі випробувань частость події сходиться по ймовірності до ймовірності події».
Графічно закон великих чисел (і його окремий випадок) представлений на рис. 5.1.
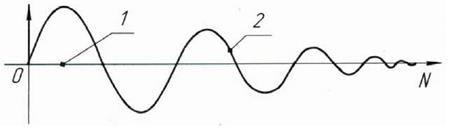
1 – математичне сподівання випадкової величини ![]() (ймовірність події Р), 2 – середнє арифметичне значень спомтережень
(ймовірність події Р), 2 – середнє арифметичне значень спомтережень![]() (частота події
(частота події ![]() )
)
Рисунок 5.1 – Графічне зображення закону великих чисел
З рис. 5.1 випливає, що в міру збільшення числа випробувань середнє арифметичне значень спостережень випадкової величини ![]() і частость події
і частость події ![]() асимптотично і необмежено наближається до математичного сподівання
асимптотично і необмежено наближається до математичного сподівання ![]() і ймовірності події Р.
і ймовірності події Р.
Це означає, що якщо справити велике число випробувань, то одержувані статистичні характеристики (середні значення) можуть розглядатися як істинні. Зазначене положення і становить математичну основу методу статистичного моделювання, тобто методу Монте-Карло.
Отже, ідея методу Монте - Карло проста і полягає в наступному: виробляється «розіграш» процесу (явища) за допомогою спеціально організованої процедури, який дає випадковий результат. Кожен «розіграш» дає нову, відмінну від інших, реалізацію досліджуваного процесу. Якщо таких реалізацій проведено багато, то ці безліч реалізацій можна використовувати як статистичний матеріал, обробивши який методами математичної статистики, отримуємо характеристики які нас цікавлять: ймовірності станів, математичне сподівання і т.д.
5.2 Моделювання випадкових чисел
5.2.1 Генерування випадкових чисел
При моделюванні процесів автомобільного транспорту найбільш проста і поширена є рівномірна випадкова послідовність чисел в інтервалі від 0 до 1.
Для отримання (генерування) рівномірно розподілених випадкових чисел існує кілька методів:
а) якщо моделювання здійснюється вручну (без допомоги ЕОМ), то для отримання випадкових чисел від 0 до 1 використовують таблиці випадкових чисел, складені за допомогою якого-небудь генератора випадкових чисел, наприклад, рулетки, апарату жеребкування і т. д.;
б) якщо розрахунок ведеться з використанням ЕОМ, то вона сама видає випадкові числа за допомогою генератора випадкових чисел.
в) метод використання спеціальних програм.
Алгоритм і блок-схема (рис. 5.2) однієї зі спеціальних програм для обчислення випадкових чисел, рівномірно розподілених в інтервалі (0, 1), можуть мати наступний зміст.
1. Вибирається довільна пара дійсних чисел Р і D.
2. Задається число Е = I.
3. Обчислюються допоміжні числа: В = D + Е і А = В / Р.
4. Приймається за випадкове число R, дрібна частина числа А.
5. Обчислюється випадковий множник Е = В - РZ, де Z - ціла частина числа А.
6. Процес повторюється, починаючи з 3-го пункту.
7. В результаті виконання алгоритму виходить нескінченна послідовність чисел, яка розглядається як випадкова, рівномірно розподілена в інтервалі (0, 1).
У процесі роботи за програмою задаються наступні вихідні дані: Р і D - пара дійсних чисел; М - необхідна кількість випадкових чисел.
У результаті роботи за програмою отримаємо:
вихідні дані Р = 5.9; В = 4.5; М = 8
рівномірно розподілені випадкові числа:
R (1) = 762712; R (2) = 432204; R (3) = 944916; R (4) = 252123
R (5) = 134554; R (6) = 605492; R (7) = 724714; R (8) = 261211
5.2.2 Дискретна випадкова величина
Розглянемо порядок моделювання дискретної випадкової величини (discrete random variable) на прикладі.
Приклад. Задана випадкова дискретна величина Х своїм рядом розподілу (табл. 5.1).
Таблиця 5.1 – Випадкова дискретна величина Х
№ п/п |
Параметр |
Позначення |
Значення |
||
1 |
Приватні значення випадкової величини |
|
3 |
5 |
7 |
2 |
Вірогідність, що відповідають значенням випадкової величини |
|
0,26 |
0,40 |
0,34 |
3 |
Інтегральна функція |
|
0,26 |
0,66 |
1,00 |
Потрібно: промоделювати випадкову величину, що відповідає цьому закону розподілу.
Розв’язок: будуємо графік інтегральної функції дискретної випадкової величини. Для цього по осі абсцис відкладаємо приватні значення випадкової величини ![]() а по осі ординат - відповідають їм ймовірності
а по осі ординат - відповідають їм ймовірності ![]() , (рис. 5.3).
, (рис. 5.3).
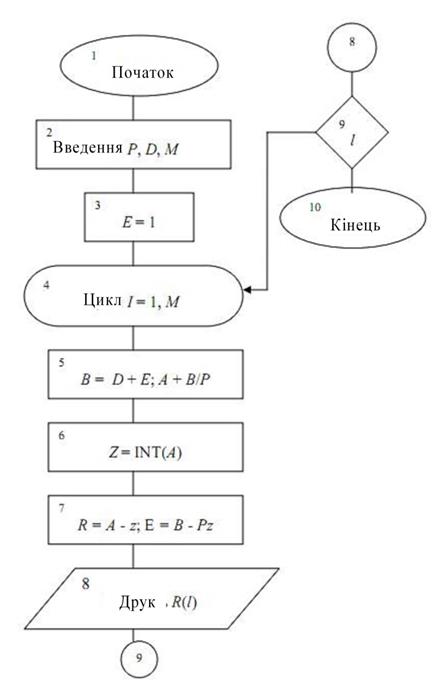
Рисунок 5.2 – Блок – схема алгоритму моделювання рівномірно розподілених випадкових чисел в інтервалі (0, 1)
При цьому ми розуміємо, що значенням ![]() відповідають:
відповідають:
![]() - від 0 до 0,26 включно відповідає
- від 0 до 0,26 включно відповідає ![]() ;
;
![]() - від 0,26 до 0,66 відповідає
- від 0,26 до 0,66 відповідає ![]() ;
;
![]() - від 0,66 до 1,00 відповідає
- від 0,66 до 1,00 відповідає ![]() .
.
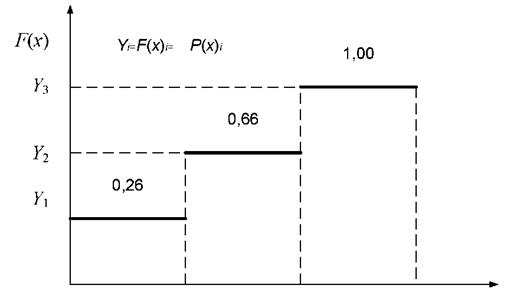
Рисунок 5.3 – Графік функції розподілу ймовірностей дискретної
випадкової величини
Скористаємося випадковими рівномірно розподіленими числами в інтервалі (![]() ), запишемо їх в перший рядок табл. 5.2. Кожному із зазначених чисел відповідає цілком певне значення
), запишемо їх в перший рядок табл. 5.2. Кожному із зазначених чисел відповідає цілком певне значення ![]() (табл. 5.2).
(табл. 5.2).
Таблиця 5.2 – Випадкові рівномірно розподілені числа
0,10 |
0,09 |
0,73 |
0,25 |
0,33 |
0,76 |
0,52 |
0,01 |
|
|
3 |
3 |
7 |
3 |
5 |
7 |
5 |
3 |
Алгоритм моделювання дискретної випадкової величини, заданої своїм рядом розподілу, містить наступні дії.
- Обчислюємо значення накопичених ймовірностей за формулою
![]() (5.3)
(5.3)
і будуємо відповідний їм графік.
2. Встановлюємо значення випадкових чисел, рівномірно розподілених в інтервалі (![]() ).
).
3. Для кожного з чисел за графіком ![]() (див. рис. 5.3) знаходимо значення
(див. рис. 5.3) знаходимо значення ![]() , що відповідають їм і представляють окремі реалізації даної випадкової величини
, що відповідають їм і представляють окремі реалізації даної випадкової величини ![]() .
.
Якщо дискретна величина задана достатньо довгим рядом розподілу і якщо при цьому потрібно, щоб, результат обчислень мало відрізнявся від істинного значення, то в цьому випадку від ручного моделювання переходять до машинного, тобто обчислення ведуть за допомогою ЕОМ.
5.2.3 Безперервна випадкова величина
Якщо випадкова величина Т неперервна (continuous random variable) і відома густина імовірності розпаділу її ![]() , то моделювання значень Т здійснюється наступною процедурою:
, то моделювання значень Т здійснюється наступною процедурою:
а) перейти від густини імовірності ![]() до функції розподілу
до функції розподілу ![]() за формулою:
за формулою: ![]() ;
;
б) потім знайти для функції F обернену їй функцію ![]() ;
;
в) вибрати випадкове число Я, від 0 до 1 і взяти від нього цю обернену функцію;
![]() .
.
Доводиться, що випадкова величина Т має як раз необхідний нам розподіл. Графічно процедура вибору випадкової величини ![]() має вигляд (рис. 5.4).
має вигляд (рис. 5.4).
Вибирається випадкове число ![]() , від 0 до 1 і для нього шукається випадкова величина
, від 0 до 1 і для нього шукається випадкова величина ![]() , при якій
, при якій ![]() (на рис. 5.5 показано стрілкою).
(на рис. 5.5 показано стрілкою).
Приклад. Потрібно розіграти випадкову величину Т, яка має закон розподілу ![]() – показовий закон. Тут Т – випадкова величина (інтервал часу між заявками на обслуговування, що надходять, час обслуговування одної заявки і т.д.);
– показовий закон. Тут Т – випадкова величина (інтервал часу між заявками на обслуговування, що надходять, час обслуговування одної заявки і т.д.); ![]() – густина розподілу випадкової величини.
– густина розподілу випадкової величини.
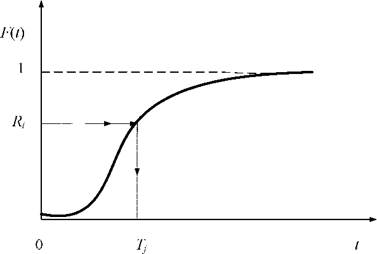
Рисунок 5.4 – Графік функції розподілу ймовірностей неперервної випадкової величини
1) Знайдемо функцію розподілу - ![]()
![]() (5.1)
(5.1)
При t=0 F(t)=0
t=∞ F(t)=1;
F(t)=0…1=![]()
2) Обчислимо обернену функцію ![]() і за нею обчислимо випадкову величину
і за нею обчислимо випадкову величину ![]() , так як F(t) =
, так як F(t) = ![]() = у, то
= у, то ![]() = 1 - у.
= 1 - у.
Логарифмуючи останній вираз, отримаємо ![]() =
= ![]() , звідки
, звідки
![]() чи
чи ![]() , де
, де![]() (5.2)
(5.2)
Алгоритми моделювання випадкових величин, які розподілені за основними ймовірнісними законами, наведені в табл. 5.3.
Таблиця 5.3 – Алгоритми моделювання випадкових величин
Ймовірнісний закон |
Густина ймовірності |
Алгоритм |
Показовий закон |
|
|
Закон Релея |
|
|
Закон Вейбулла |
|
|
Закон рівномірної густини |
|
|
Нормальний закон |
|
|
5.3 Розв’язок задач теорії масового обслуговування
5.3.1 Часткові питання моделювання випадкових процесів
Розглянуті вище способи моделювання різних випадкових величин дозволяють застосовувати метод Монте-Карло для вирішення різних інженерних і економічних завдань. Так, наприклад, він може засьлслвуватися для визначення числових характеристик функціонування складних стохастичних процесів. Часто метод Монте-Карло застосовують для вирішення задач теорії масового обслуговування не потрапляють під марківський випадковий процес.
При дослідженні характеристик функціонування систем масового об-слуговування (СМО) методами статистичного моделювання часто прихо-диться розігрувати інтервали часу прибуття заявок на обслуговування і час обслуговування заявки розподілених по тому або іншому вероятностному законом. Для реалізації цих процесів визначається одним з відомих методів рівномірно розподілені випадкові числа ![]() в інтервалі від 0 до 1.
в інтервалі від 0 до 1.
Далі визначаємо інтервали часу прибуття заявок на СМО по виразу
![]() (5.3)
(5.3)
і час обслуговування i-ої заявки –
![]() , (5.4)
, (5.4)
Припустимо, що СМО має два канали обслуговування та два місця в черзі. Для даної СМО, залежно від величин ![]() і
і ![]() , можемо мати чотири варіанти її функціонування.
, можемо мати чотири варіанти її функціонування.
1 варіант. Припустимо, що при моделюванні випадкових моментів надходження вимог на обслуговування і випадкового часу обслуговування заявок було отримано такі числа у хвилинах:
![]() = 0; 25, 30, 40, 50 і т.д.;
= 0; 25, 30, 40, 50 і т.д.;
![]() = 20, 22, 25, 30 і т.д.
= 20, 22, 25, 30 і т.д.
Отримані значення часу відкладемо на відповідних осях рис. 5.5.
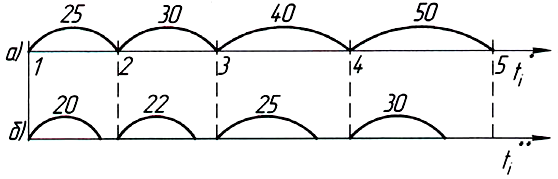
а – час надходження заявок; б – час обслуговування заявок
Рисунок 5.5 – Схема роботи СМО
При цих умовах буде працювати тільки перший канал. Другий канал буде простоювати без роботи і заявок, які очікують у черзі, не буде.
2 варіант. Припустимо, що при моделюванні випадкових моментів надходження заявок і випадкового часу обслуговування були отримані наступні числа у хвилинах:
![]() = 0; 20; 18; 15 і т.д.
= 0; 20; 18; 15 і т.д.
![]() = 25; 30; 17 і т.д.
= 25; 30; 17 і т.д.
Отримані значення часу відкладемо на відповідних осях рис. 5.6.
За цих умов, як видно з рис. 5.6, будуть працювати обидва канали. Заявок, що чекали в черзі, не буде.
3 варіант. Припустимо, що при моделюванні випадкових моментів надходження заявок і часу обслуговування були отримані наступні числа:
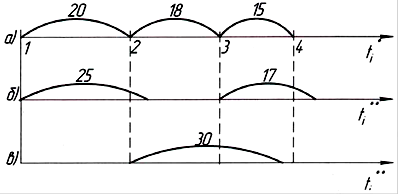
а – час надходження заявок; б – час обслуговування заявок першим
каналом; в – час обслуговування другим каналом
Рисунок 5.6 – Схема роботи СМО
![]() = 0; 20; 50; 60 і т.д.
= 0; 20; 50; 60 і т.д.
![]() = 3 години; 2 години; 1 годину 20 хв.; 1 годину 40 хв. і т.д.
= 3 години; 2 години; 1 годину 20 хв.; 1 годину 40 хв. і т.д.
Отримані числа відкладемо на відповідних осях рис. 5.7.
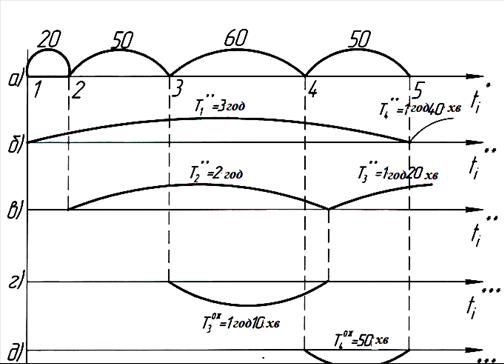
а - час надходження заявки, б - час обслуговуванні першої та четвертої заявок; в - час обслуговування другої і третьої заявок; г - час перебування в черзі третьої заявки; д - час перебування в черзі четвертої заявки
Рисунок 5.7 – Схема роботи СМО
![]() = 4 години; 3 години 40 хв.; 4 години 5 хв.; 4 години 10 хв. і т.д.
= 4 години; 3 години 40 хв.; 4 години 5 хв.; 4 години 10 хв. і т.д.
Для заданих умов працюватимуть обидва канали. Третя і четверта заявки будуть очікувати в черзі. Оскільки СМО передбачено два місця в черзі, тому обидві заявки (третя і четверта) будуть обслужені.
4 варіант. Припустимо, що при моделюванні випадкових моментів надходження заявок і випадкового часу обслуговування їх було отримано такі числа:
![]() = 0; 20; 50; 40; 20; 20 і т.д.
= 0; 20; 50; 40; 20; 20 і т.д.
Отримані числа відкладемо на відповідних осях рис. 5.8.
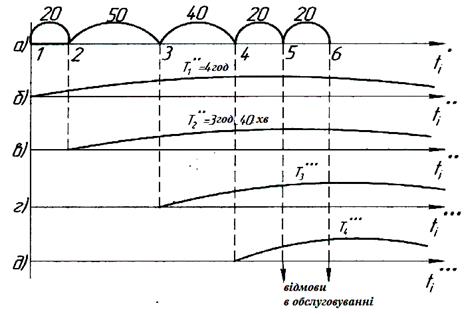
а - час надходження заявки, б - час обслуговувань першої заявки; в - час обслуговування другої заявки; г - час перебування в черзі третьої заявки;
д - час перебування в черзі четвертої заявки
Рисунок 5.8 – Схема роботи СМО
З рис. 5.8 видно, що для заданих умов працюватимуть обидва ка-налу. Третя і четверта заявки будуть стояти в черзі. Оскільки СМО передбачає лише два місця в черзі, то п'ята і шоста заявки отримують відмову в обслуговуванні і підуть необслуженими.
Слід врахувати, що в СМО можуть бути накладені і інші умови на освіту черги.
5.3.2 Алгоритм розв’язання задач з визначенню числових характеристик систем масового обслуговування
Розглянемо на прикладі порядок застосування методу статистичного моделювання для визначення числових характеристик функціонування станції технічного обслуговування автомобілів (СТОА).
Приклад. Досліджується ефективність роботи СТОА, що має в своєму розпорядженні N постів. Станція починає працювати в ![]() = 8.00 і закінчує в
= 8.00 і закінчує в ![]() = 20.00. Станція працює за схемою з очікуванням прибулих машин в черзі з обмеженням за часом.
= 20.00. Станція працює за схемою з очікуванням прибулих машин в черзі з обмеженням за часом.
Статистичними спостереженнями встановлено, що автомобілі при-бувають на станцію у випадкові моменти часу ![]() , при цьому час між двома автомобілями розподілено за законом Вейбулла з параметрами n, λ,
, при цьому час між двома автомобілями розподілено за законом Вейбулла з параметрами n, λ, ![]() . Час, який витрачається на обслуговування ав-томобілів
. Час, який витрачається на обслуговування ав-томобілів ![]() , випадковий і розподілений за законом Релея з параметром ν. Час перебування в черзі
, випадковий і розподілений за законом Релея з параметром ν. Час перебування в черзі ![]() випадковий і розподілений по показовому закону з параметром ν.
випадковий і розподілений по показовому закону з параметром ν.
Вхідними даними для вирішення поставленого завдання служать: λ, µ, ν, одержувані на основі статистичної обробки експериментальних даних.
Для зазначених умов потрібно знайти числові характеристики функціонування системи:
-кількість обслуговуваних автомобілів,
-число автомобілів, які очікують у черзі,
-число автомобілів, які покидають чергу необслуженими.
Розвязок. З огляду на те, що потік вимог на обслуговування не є пуассоновським, а час обслуговування розподілено не по показовому закону, завдання не може бути вирішене за допомогою основних положень теорії масового обслуговування. Приймемо для її вирішення метод статиститичного моделювання. Цільова функція в розглянутій задачі являє собою продуктивність роботи станції за один робочий день, є функція багатьох випадкових аргументів.
![]() , (5.5)
, (5.5)
де ![]() - початок роботи станції;
- початок роботи станції;
![]() - кінець робочого дня.
- кінець робочого дня.
З огляду на те, що розглянута задача являє собою деякий процес у часі, тому моделювання роботи станції будемо здійснювати в дискретної схемою з кроком дискретності, рівному одному місяцю. Це означає, що інформація про перебіг процесу буде видаватися на перше число кожного поточного місяця. Вирішення завдання покажемо на рисунку 5.9.
5.3.3 Дослідження характеристик функціонування станції технічного обслуговування автомобілів методом Монте-Карло
Розглянемо на прикладі порядок застосування методу статистичного моделювання для визначення числових характеристик функціонування станції технічного обслуговування (СТОА).
Приклад. Досліджується СТОА методом статистичного моделювання для однієї реалізації, яка має два канали і два місця для очікування в черзі. Інтенсивність надходження заявок λ = 1,5 заявки на годину, інтенсивність обслуговування одного каналу µ = 0,5 заявки на годину.
1. Складаємо розмічений граф станів (рис. 5.9).
де ![]() - всі канали вільні;
- всі канали вільні;
![]() - Зайнятий один канал;
- Зайнятий один канал;
![]() - Зайняті обидва канали;
- Зайняті обидва канали;
![]() - Обидва канали зайняті і одна заявка в черзі;
- Обидва канали зайняті і одна заявка в черзі;
![]() - Обидва канали зайняті і дві заявки в черзі.
- Обидва канали зайняті і дві заявки в черзі.
2. Розігруємо інтервали часу прибуття і час обслуговування заявок, для чого скористаємося алгоритмом моделювання випадкової величини Т, розподіленої за показовим законом, тобто
![]() ;
; ![]() (5.6)
(5.6)
де ![]() — інтервал часу надходження заявок на СМО;
— інтервал часу надходження заявок на СМО;
![]() - час обслуговування і-ої заявки.
- час обслуговування і-ої заявки.
λ λ λ λ
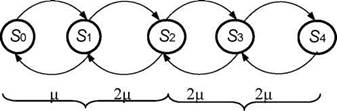
до появи черги після появи черги
Рисунок 5.9 – Розмічений граф станів
Випадкові числа ![]() від 0 до 1 беремо з таблиць 1 і 2 (Додатки).
від 0 до 1 беремо з таблиць 1 і 2 (Додатки).
Складаємо таблицю часу прибуття і часу обслуговування заявок (табл. 5.4) і зображуємо процедуру моделювання графічно (рис. 5.9).
Для графічного зображення процесу моделювання роботи СМО візьмемо кілька координатних осей, які мають один і той же масштаб відліку часу. На першій осі відкладемо астрономічний час, на другий відзначимо моменти надходження заявок на обслуговування. На осі ![]() зобразимо стан системи, коли всі канали вільні, на осях
зобразимо стан системи, коли всі канали вільні, на осях ![]() і
і ![]() - стан першого і другого каналів, на осях
- стан першого і другого каналів, на осях ![]() і
і ![]() - стан першого і другого місць у черзі.
- стан першого і другого місць у черзі.
До моменту ![]() - надходження першої заявки всі канали і всі місця в черзі вільні. У момент приходить перша заявка і займає перший канал. Скільки часу він буде зайнятий, вирішується розігруванням.
- надходження першої заявки всі канали і всі місця в черзі вільні. У момент приходить перша заявка і займає перший канал. Скільки часу він буде зайнятий, вирішується розігруванням.
Перше розігране значення часу обслуговування відкладаємо на осі ![]() від точки з абсцисою
від точки з абсцисою ![]() , відзначаємо його жирною лінією. У момент
, відзначаємо його жирною лінією. У момент
![]() - приходу другої заявки перший канал зайнятий, заявка займає другий канал. Розігруємо ще одне значення
- приходу другої заявки перший канал зайнятий, заявка займає другий канал. Розігруємо ще одне значення ![]() - і позначаємо жирною лінією
- і позначаємо жирною лінією
на осі ![]() від точки з абсцисою
від точки з абсцисою ![]() і т.д.
і т.д.
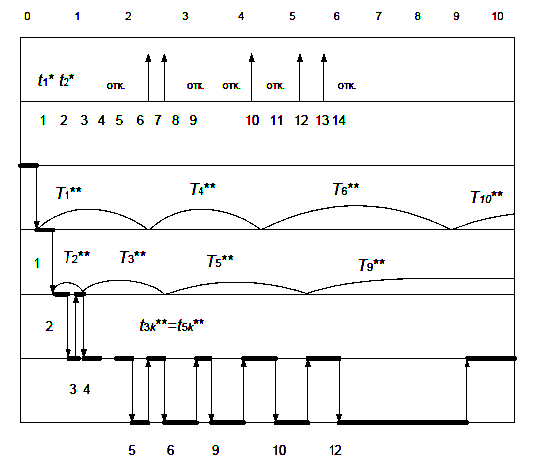
Рисунок – 5.10. Графічний процес моделювання
Заявка, що прийшла в момент, коли всі канали і місця в черзі зайняті, отримує відмову (вона покидає СМО необслуженою).
Припустимо, що моделювання реалізації продовжено нами досить довго. Визначимо ймовірні характеристики СМО. Імовірності ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() того, що система знаходиться в стані
того, що система знаходиться в стані ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , знайдемо з відношень:
, знайдемо з відношень:
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() (5.7)
(5.7)
де ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() - суми часу знаходження системи в станах
- суми часу знаходження системи в станах ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() (беруться з даних рис. 5.10);
(беруться з даних рис. 5.10);
Т - розглядуваний інтервал часу (8 годин).
Очевидно, ![]() +
+ ![]() +
+ ![]() +
+ ![]() +
+ ![]() = Т.
= Т.
Імовірність відмови знайдеться на великому проміжку часу Т як відношення числа ![]() заявок, що отримали відмову, до загального числа заявок, що надійшли в цей час:
заявок, що отримали відмову, до загального числа заявок, що надійшли в цей час:
![]() (5.8)
(5.8)
- відносна пропускна здатність
Таблиця 5.4 – Час надходження та обслуговування
Час надходження
Номер заявки (розіграшу) |
№ |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
Випадкове число |
|
37 |
54 |
20 |
48 |
05 |
64 |
89 |
47 |
42 |
96 |
24 |
80 |
Проміжок часу між двома |
|
0,23 |
0,39 |
0.11 |
0,33 |
0.02 |
0.51 |
1.11 |
0.32 |
0.27 |
1.62 |
0.14 |
0.81 |
Момент надходження |
|
0,23 |
0,62 |
0,73 |
1,06 |
1,08 |
1,59 |
1,70 |
2,02 |
2,29 |
3,90 |
4,04 |
4,85 |
Час обслуговування
Номер заявки |
№ |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
Випадкове число |
|
47 |
25 |
44 |
52 |
66 |
95 |
27 |
0,7 |
99 |
53 |
59 |
36 |
Час обслуговування |
|
1,27 |
0,32 |
1,16 |
1,47 |
2,16 |
5,99 |
0,63 |
0,15 |
9,21 |
1,51 |
1,78 |
0,89 |
Початок обслуговування |
|
0,23 |
0,62 |
0,94 |
1,50 |
2,10 |
2,97 |
Відмова |
Відмова |
4,26 |
8,96 |
Відмова |
10,47 |
Кінець обслуговування |
|
1,50 |
0,94 |
2,10 |
2,97 |
4,26 |
8,96 |
13,57 |
10,47 |
11,36 |
![]() ; (5.9)
; (5.9)
- абсолютна пропускна здатність:
![]() ; (5.10)
; (5.10)
- cереднє число зайнятих каналів:
![]() ; (5.11)
; (5.11)
- cереднє число заявок в черзі:
![]() . (5.12)
. (5.12)
5.4 Моделювання потреби підприємства в запасних частинах
При плануванні та управлінні рівнів запасних частин (вузлів, агрегатів) на складах АТП (центральному, проміжному, оборотних аг-регату) у ряді випадків необхідно враховувати кілька випадкових факторів, які мають місце в процесі функціонування технічної служби та служби постачання підприємства. До них відносяться: випадковий час відмови автомобіля, випадковий час поповнення запасів, випадкові величини потреби та обсяги поповнення запасних частин. Тому в практиці розрахунків потреби запасних частин широке поширення знайшов метод статистичних випробувань (метод Монте-Карло), дозволяючий моделювати будь-який процес, на протікання якого впливають випадкові фактори.
Розрахунок потреби в запасних частинах (вузлах, агрегатах) методом статистичного моделювання розглянемо на прикладі роботи складу, з якого в довільний момент часу t на вимогу видається випадкова кількість агрегатів (вузлів, запасних частин) одного найменування ![]() . Якщо в даний момент t запас X на складі достатній, то запит
. Якщо в даний момент t запас X на складі достатній, то запит ![]() задовольняється повністю. Якщо запас недостатній для повного задоволення вимоги, то він задовольняється лише на величину запасу, наявного на складі. В останньому випадку підприємство несе втрати від дефіциту, величина яких пропорційна кількості недоданих технічної службі агрегатів, тобто
задовольняється повністю. Якщо запас недостатній для повного задоволення вимоги, то він задовольняється лише на величину запасу, наявного на складі. В останньому випадку підприємство несе втрати від дефіциту, величина яких пропорційна кількості недоданих технічної службі агрегатів, тобто ![]() де к - втрати підприємства через простій одного автомобіля при дефіциті агрегатів на складі.
де к - втрати підприємства через простій одного автомобіля при дефіциті агрегатів на складі.
Надходження агрегатів на склад підприємства від постачальників відбувається також у випадкові моменти часу τ й у випадковому обсязі ![]() . Затрати на утримання та зберігання агрегатів на складі
. Затрати на утримання та зберігання агрегатів на складі ![]() , де λ - вартість зберігання і утримання одного агрегату на складі за період Т;
, де λ - вартість зберігання і утримання одного агрегату на складі за період Т; ![]() - середній запас на складі за період Т.
- середній запас на складі за період Т.
Необхідно знайти такий плановий рівень початкового запасу агрегатів ![]() на складі, при якому сумарні витрати підприємства будуть мінімальними (рис. 5.11)
на складі, при якому сумарні витрати підприємства будуть мінімальними (рис. 5.11) ![]() Min.
Min.
Таким чином, тут мають місце чотири випадкові величини: момент надходження вимоги на відпустку агрегатів зі складу t; обсяг цієї вимоги ![]() ; момент надходження агрегатів на склад від постачальників τ і обсяг цієї поставки
; момент надходження агрегатів на склад від постачальників τ і обсяг цієї поставки ![]() .
.
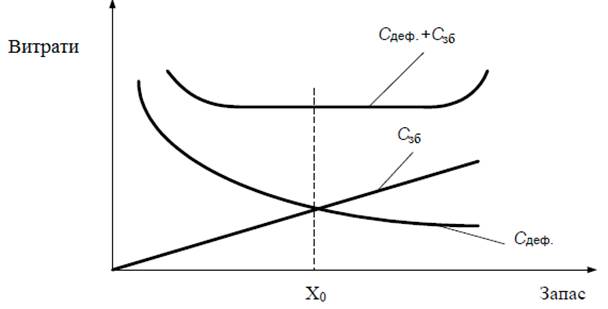
Рисунок 5.11 – Залежність витрат підприємств від величини початкового запасу
Закони розподілу зазначених випадкових величин установлюються на основі обробки інформації, що міститься у картках складського обліку.
Для подальшого вирішення завдання введемо величини:
![]() - тривалість інтервалу між (i + 1)-й і i-й видачею агрегатів зі складу;
- тривалість інтервалу між (i + 1)-й і i-й видачею агрегатів зі складу;
![]() - тривалість інтервалу між (i + 1)-й і i-й постачальниками агрегатів на склад.
- тривалість інтервалу між (i + 1)-й і i-й постачальниками агрегатів на склад.
Так як ![]() і
і ![]() - величини випадкові, отже, величини
- величини випадкові, отже, величини ![]() та
та ![]() будуть також випадковими.
будуть також випадковими.
Для вирішення даної задачі необхідні вихідні дані, в якості яких можуть служити різні значення планового рівня початкового запасу агрегатів ![]() . Розрахунки на ЕОМ при різних вихідних даних по всьому плановому періоду Т (рік) дозволяють імітувати реальні процеси, протікаючі на підприємстві, для чого значення випадкових величин встановлюємо за допомогою генератора випадкових чисел, закон розподілу яких повинен відповідати закону розподілу випадкових величин по даному підприємству. У результаті розрахунків по всіх вибраних рівням початкового запасу
. Розрахунки на ЕОМ при різних вихідних даних по всьому плановому періоду Т (рік) дозволяють імітувати реальні процеси, протікаючі на підприємстві, для чого значення випадкових величин встановлюємо за допомогою генератора випадкових чисел, закон розподілу яких повинен відповідати закону розподілу випадкових величин по даному підприємству. У результаті розрахунків по всіх вибраних рівням початкового запасу ![]() виявляємо залежність сумарних витрат за весь період по зберіганню запасу агрегатів і через дефіцит у разі відмови у задоволенні потреб через відсутність агрегатів на складі.
виявляємо залежність сумарних витрат за весь період по зберіганню запасу агрегатів і через дефіцит у разі відмови у задоволенні потреб через відсутність агрегатів на складі.
5.5 Моделювання оптимальної періодичності технічних впливів
Періодичність технічних впливів (ТВ) (frequency of impacts) це нормативне напрацювання (у кілометрах пробігу або годинах роботи) між двома послідовними проведеними однорідними роботами ТО або ТР.
Розрізняють такі методи визначення (коригування) періодичності ТВ: найпростіші (методи аналогії по прототипу); аналітичні, засновані на результатах спостережень і основних закономірностях ТЕА; імітаційні, засновані на моделюванні випадкових про-процесів.
Найбільш розробленими і переважними є аналітичні методи визначення періодичності ТВ, до яких відносяться:
а) метод визначення періодичності ТВ по допустимому рівню безвідмовності заснований на виборі такої раціональної періодичності ТО, при якій ймовірність відмови F елемента не перевищує заздалегідь заданої величини званої ризиком (рис. 5.12).
Ймовірність безвідмовної роботи ![]() , при якій напрацювання на відмову більше призначеної періодичності обслуговування lo визначає безвідмовність елемента автомобіля:
, при якій напрацювання на відмову більше призначеної періодичності обслуговування lo визначає безвідмовність елемента автомобіля:
![]() , тобто
, тобто ![]() , (5.14)
, (5.14)
де ![]() - напрацювання на відмову;
- напрацювання на відмову;
![]() - допустима ймовірність безвідмовної роботи;
- допустима ймовірність безвідмовної роботи;
![]() ;
;
![]() -
- ![]() - відсотковий ресурс;
- відсотковий ресурс;
F - ймовірність відмови.
Для агрегатів і механізмів, що забезпечують безпеку руху, ![]() = 0,90 - 0,98. Для інших вузлів і агрегатів, RД = 0,65 - 0,90;
= 0,90 - 0,98. Для інших вузлів і агрегатів, RД = 0,65 - 0,90;
б) техніко-економічний метод зводиться до визначення сумарних питомих витрат на ТО та ремонт автомобілів і їх мінімізації. Мінімальним сумарним витратам відповідає оптимальна періодичність технічного обслуговування ![]() . При цьому питомі витрати на ТО:
. При цьому питомі витрати на ТО:
![]() , (5.15)
, (5.15)
де l - періодичність ТО;
d - вартість виконання операцій ТО.
Збільшення періодичності ТО, як правило, призводить до скорочення ресурсу елемента і зростання питомих витрат на ремонт.
![]() , (5.16)
, (5.16)
де С - разові витрати на ремонт; L = l - періодичність.
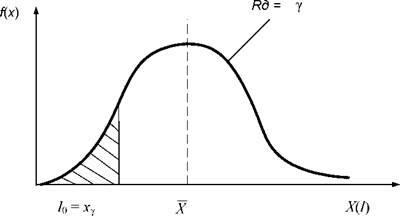
Рисунок 5.12 – Визначення періодичності ТВ по допустимому рівню безвідмовності
Вираз ![]() min є цільовою функцією, екстремальне значення якої відповідає оптимальному рішенню. Визначення мінімуму цільової функції і оптимальності lо = lопт значення періодичності ТО проводиться графіком (рис. 5.13).
min є цільовою функцією, екстремальне значення якої відповідає оптимальному рішенню. Визначення мінімуму цільової функції і оптимальності lо = lопт значення періодичності ТО проводиться графіком (рис. 5.13).
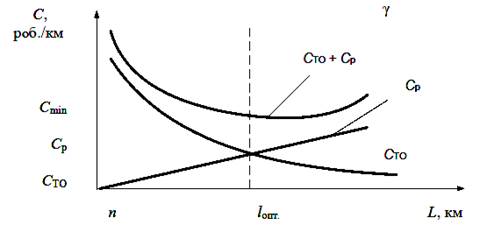
Рисунок 5.13 – Графік оптимізації періодичності ТБ техніко-економічним методом
5.5.1 Моделювання оптимальної періодичності технічних впливів за допустимим рівнем безвідмовності
У процесі роботи групи автомобілів виникають відмови конкретного вузла, механізму автомобіля, напрацювання яких ![]() , випадкова і підпорядковується одному з відомих законів розподілу: f(х);
, випадкова і підпорядковується одному з відомих законів розподілу: f(х);![]() ;
; ![]() ;
; ![]() . За даним вузлу, механізму може виконуватися попереджувальне технічне обслуговування з встановленою періодичністю l. У реальних умовах фактична періодичність ТО
. За даним вузлу, механізму може виконуватися попереджувальне технічне обслуговування з встановленою періодичністю l. У реальних умовах фактична періодичність ТО ![]() , головним чином через зміни середньодобового пробігу автомобілів також має деяку варіацію і характеризується законом розподілу φ(l),
, головним чином через зміни середньодобового пробігу автомобілів також має деяку варіацію і характеризується законом розподілу φ(l),![]() ;
;![]() і
і ![]() . Якщо періодичність визначається за допустимого рівня безвідмовності, то завдання формулюється таким чином. Необхідно визначити оптимальну періодичність ТО
. Якщо періодичність визначається за допустимого рівня безвідмовності, то завдання формулюється таким чином. Необхідно визначити оптимальну періодичність ТО ![]() , при якій ймовірність безвідмовної роботи буде не нижче заданої, тобто
, при якій ймовірність безвідмовної роботи буде не нижче заданої, тобто ![]() .
.
Розглянутий процес, відбувається під дією довільного потоку подію, то його математичну модель побудувати важко. У цьому випадку можна використовувати метод статистичного моделювання (метод Монте- Карло).
Розглянута вище методика дозволяє отримати випадкові величини ![]() і
і ![]() розподілені відповідно по законам f(x) і φ(l).
розподілені відповідно по законам f(x) і φ(l).
Отже, очевидний сенс імітаційного моделювання оптимізації періодичності в розглянутому прикладі складається:
а) у відтворенні і фіксації двох можливих подій:
А - відмови автомобіля, якщо ![]() <
< ![]() ;
;
Б - виконання ТО, тобто попередження відмови, якщо ![]() >
>![]() ;
;
б) визначенні ймовірностей цих подій, відповідно Р (А) = F (відмова) і Р (Б) = R (профілактика);
в) порівнянні фактичного (R) і заданого значення ймовірності безвідмовної роботи (![]() ).
).
5.5.2 Моделювання оптимальної періодичності технічних впливів за економічними показниками
Так як цільова функція техніко-економічного методу оптимізації періодичності технічного обслуговування елементів автомобіля в загальному вигляді описується виразом:
![]() , (5.17)
, (5.17)
де ![]() - середня (питома) вартість ремонту і технічного обслуговування;
- середня (питома) вартість ремонту і технічного обслуговування;
![]() - середня вартість усунення відмови;
- середня вартість усунення відмови;
![]() =
= ![]() - середнє напрацювання на відмову;
- середнє напрацювання на відмову;
![]() =
= ![]() - середня вартість операції технічного обслуговування;
- середня вартість операції технічного обслуговування;
![]() - напрацювання на виконання операцій технічного обслуговування.
- напрацювання на виконання операцій технічного обслуговування.
Тому при моделюванні оптимальної періодичності ТО необхідно мати дані:
[x] - масив напрацювання на відмову;
[l] - Масив напрацювання на виконання операцій ТО;
[c] - масив разових витрат на усунення відмови;
[d] - масив разових витрат виконання операцій ТО.
Послідовність імітаційного моделювання оптимальної періодичності ТО розглядаються методом зображена на рис. 5.14 і включає такі елементи:
1) завдання вихідних даних: [x], [l], [c], [d], М (блок 1);
2) генерування і реалізація ![]() ,
,![]() ,
, ![]() ,
, ![]() (блоки 2 - 8);
(блоки 2 - 8);
3) ідентифікація подій: ![]() <
< ![]() - відмова (блок 9),
- відмова (блок 9), ![]() >
> ![]() - профілактика (блок 11);
- профілактика (блок 11);
4) визначення ймовірностей подій F і R ( блоки 14, 15);
5) У блоках 8, 9 і 13 визначається сумарна питома вартість ТО і ремонту однієї реалізації:
![]() . (5.18)
. (5.18)
При багаторазовому повторенні процедури моделювання в блоці 16 обчислюється середнє значення сумарної питомої вартості ТО і ремонту для вихідної періодичності за формулою:
![]() , C (5.19)
, C (5.19)
де n - число реалізації при початковій періодичності ![]() .
.
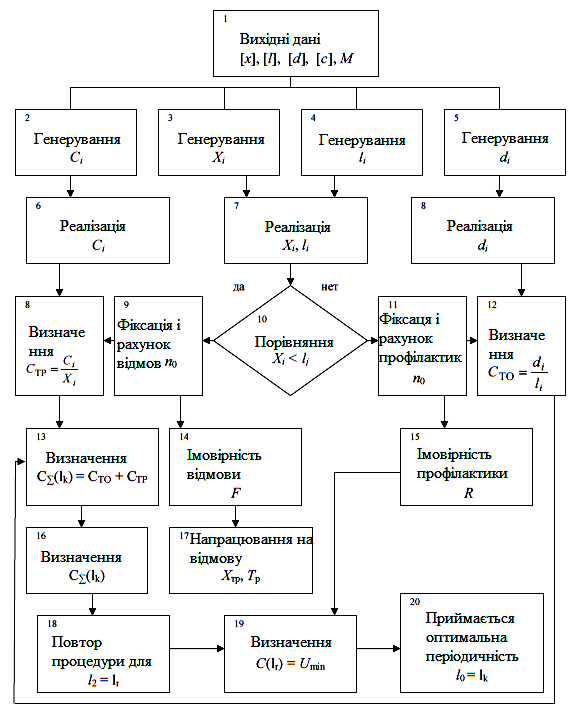
Рисунок 5.14 – Блок - схема алгоритму моделювання оптимальної
періодичності ТО техніко-економічним методом
7) Блок 18 передбачає повторення всієї процедури моделиро ¬ вання для наступних значень періодичності ТО: (![]() ;
;![]() ;
; ![]() …
… ![]() ).
).
8) У блоках 19, 20 проводиться порівняння отриманих значень ![]() та вибір оптимальної періодичності, відповідної мінімальної значенням цільової функції, тобто
та вибір оптимальної періодичності, відповідної мінімальної значенням цільової функції, тобто ![]() .
.
9) Рівень безвідмовності при оптимальному рішенні оцінюється
співвідношенням ![]() , отриманим в циклі моделювання для
, отриманим в циклі моделювання для ![]() =
= ![]() .
.
10) Замикаюча перевірка результатів здійснюється за формулою:
![]() (5.21)
(5.21)
де c і d - середні вихідні значення вартості усунення відмови і опе-рацій технічного обслуговування;
![]() - оптимальне значення періодичності ТО;
- оптимальне значення періодичності ТО;
![]() - середнє напрацювання на відмову;
- середнє напрацювання на відмову;
![]()
де z - кількість подій оптимального циклу, відповідних відмови.
Контрольні запитання
1. Перерахуйте переваги імітаційного моделювання.2. Перерахуйте основні етапи статистичного моделювання.
3. У чому сутність методу Монте-Карло.
4. Які особливості моделювання дискретної випадкової величини?
5. Які особливості моделювання безперервної випадкової величини?
6. Які типи завдань автомобільного транспорту доцільно вирішувати методом статистичного моделювання.
7. Яка послідовність розіграшу інтервалу часу прибуття заявок на обслуговування і часу обслуговування заявок.
8. Числові характеристики функціонування СТОА. Особливості моделювання функціонування СТОА методом Монте - Карло.
9. Перерахуйте випадкові чинники, які мають місце при плануванні та управлінні рівнів запасних частин на складах АТП.
10. Запишіть цільову функцію витрат підприємства від величини початкового запасу і назвіть її складові.
11. Послідовність моделювання потреби підприємства в запасних частинах.
12. Перерахуйте методи визначення та коригування періодичності технічних впливів.
13. Особливості методу визначення періодичності ТО по допустимому рівню безвідмовності елементів автомобіля.