---

---

6 МЕТОДИ МЕРЕЖЕВОГО ПЛАНУВАННЯ

Мережеве планування (network planning) – метод наукового планування та управління виробничими процесами, які виконують великі обсяги робіт.

Методи мережевого планування знаходять широке застосування в багатьох галузях народного господарства, в тому числі і на автомобільному транспорті. На автомобільному транспорті методами мережевого планування описуються процеси технічного обслуговування і ремонту автомобілей, перевізні та будівельні процеси і т.д.

Мережеве планування має ряд переваг: забезпечує наочність технологічної послідовності робіт; дозволяє скласти оперативні та поточні плани, а також прогнозувати складні процеси; дозволяє виявити приховані ресурси часу і матеріальних засобів при виконанні виробничих процесів.

Щоб приступити до мережевого планування (моделювання) того чи іншого виробничого процесу необхідно мати перелік і тривалість виконання операцій, відповідних розглядався виробничому процесу. Мережеве планування супроводжується побудовою робочих таблиць і мережевих графіків.

6.1 Основні елементи мережевих графіків

При побудові мережевих графіків використовують два логічних поняття (елемента) – робота і подія. У мережевому плануванні термін «робота» передбачає процес передує вчинення будь - якого події. Термін «подія» висловлює собою певний результат виконання роботи (або робіт).

На мережевому графіку події зображують гуртком, а роботи - орієнтованих стрілками. Частковий приклад мережевого графіка наведено на рис. 6.1.

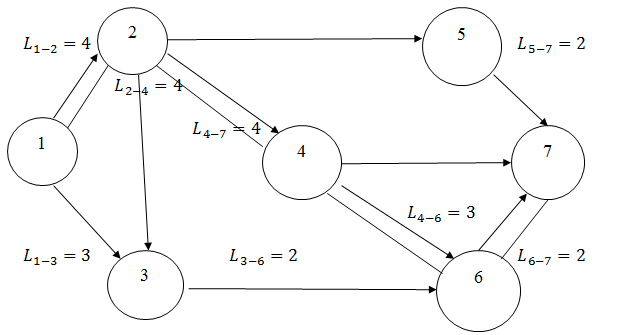
Рисунок 6.1 – Частковий приклад мережевого графіка

Кожній події присвоюється певний номер (зазвичай цифрою), тобто 1, 2, 3 і т.д. – це події. Кожна робота, зображена на мережевому графіку стрілкою, об'єднує тільки дві події, тому прийнято роботу на мережевому графіку позначати номерами попередньої (i- ої) і наступної (j-ої) подій, тобто 1 - 2, 2 - 5, 5 - 7 і т.д. – це роботи.

Тривалість роботи проставляється над стрілками, тобто L_1-2=4, L_2-5=5 і т.д. - тривалість робіт.

Мережевий графік являє собою послідовність робіт і подій, що відображають їх технологічну взаємозв'язок.

На мережевому графіку виділяють дві події: початкове (1) (вихідне) і кінцеве (7) (завершальне). Всі інші події називаються про-проміжними.

Оригінал подія відображає початок виконання всього комплексу робіт і не має попереднього події. Завершающееся подія відображає кінцеву мету всього комплексу робіт і не має подальшого події.

Термін «робота» включає три поняття:

1 «Фактична робота» - тобто трудовий процес, що приводить до досягненню певних результатів і потребують витрат часу і ресурсів;

2 «Очікування» - технологічна перерва в роботі, не вимагає витрат праці, але вимагає витрат часу (висихання фарби, затвердівання цементу і т.д.);

3- «Залежність» (фіктивна робота) - логічний зв'язок між подіями, що не вимагає витрат часу і ресурсів, але показує, що можливість початку однієї роботи залежить від результатів іншої.

На мережевих графіках фактичну роботу і очікування зображують суцільними стрілками, а залежності - пунктирними.

Мережевий графік будують в масштабі або без масштабу. В останньому випадку обов'язково над стрілками проставляють тривалість роботи в одиницях часу. Будь-яка послідовність робіт від однієї події до іншого (будь-яка) називається шляхом і позначається L (2 - 5 - 7), тобто кожен шлях позначають буквою L і номерами подій через які він проходить.

Довжина будь-якого шляху визначається сумарною тривалістю складових його робіт.

Повний шлях - це шлях від вихідного до завершального події.

У мережевому графіку, як правило, є кілька повних шляхів з різною тривалістю.

Так, для нашого прикладу маємо п'ять повних шляхів, довжина яких:

L1(1 - 2 - 5- 7) = 4 + 5 + 1 = 10;

L2(1 - 2 - 4 - 7) = 4 + 3 + 3 = 10;

L3(1 - 2 - 4 - 6 - 7) = 4 + 3 + 3 + 2 = 12;

L4(1 - 2 - 3 - 6 - 7) = 4 + 1 + 2 + 2 = 9;

L5(1 - 3 - 6 - 7) = 4 + 2 + 2 = 8.

Повний шлях, що має максимальну тривалість, називають критичним шляхом.

Роботи, що лежать на критичному шляху називається критичними роботами.

Для нашого прикладу: L_kp(1 - 2 - 4 - 6 - 7) = 12 одиниць часу. Для більшої наочності його виділяють подвійними або жирними лініями. Критичний шлях (L_kp) визначає загальну тривалість виконання всього комплексу робіт.

Повні шляху, тривалість яких менше L_kp, називаються некритичними. У них є резерв часу, в межах якого час виконання робіт може бути збільшено, що не призводить до збільшення загальної тривалості настання завершального події.

6.2 Правила побудови мережевих графіків

При побудові мережевих графіків необхідно враховувати наступні правила: 1. Між двома подіями на графіку може знаходитися тільки одна робота (рис. 6.2).

Рисунок 6.2 – Між двома подіями може знаходитися тільки одна робота

2. Якщо одна подія служить початком декількох робіт, які за-закінчуються також в одній події, то необхідно ввести фіктивні роботи і додаткові події зі своїми номерами (рис. 6.3).

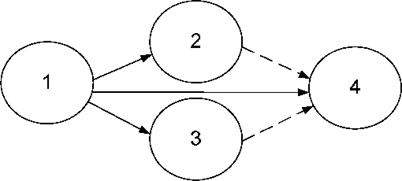
Рисунок 6.3 – Введення фіктивних робіт і додаткових подій

3. Всі події, крім завершального, повинні мати наступну роботу. Наявність «глухих кутів» у мережі вказує на помилку. Так само в мережі не повинно бути подій, в які не входять ні одна робота (виняток становить вихідні подія).

4. У мережевому графіку не повинно бути замкнутих контурів, тобто шляхів, які починаються і закінчуються в одній і тій же події.

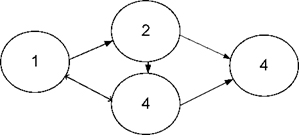
Рисунок 6.4 – Схема без замкнутих контурів

5. При побудові мережевих графіків слід уникати взаємного перетину стрілок:

 

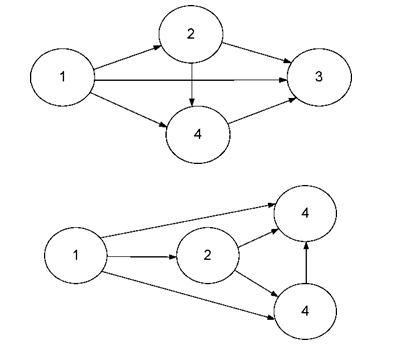
Рисунок 6.5 – Схема уникнення взаємного перетину стрілок

6.3 Процес побудови мережевих графіків

Процес мережевого планування і управління (МПУ) включає в себе чотири взаємопов'язаних етапи:

1. Опис комплексу робіт, визначення їх тривалості та послідовності.

2. Побудова мережевого графіка.

3. Розрахунок і аналіз параметрів мережного графіка.

4. Оптимізація мережевого графіка, контроль і оперативне управління ходом виконання комплексом робіт.

Приклад. Скласти мережевий графік змінно-добового плану перевезення вантажів автомобільним транспортом.

1. Визначаємо перелік робіт у складі мережевого графіка (див.
табл. 6.1).

Таблиця 6.1 – Перелік робіт у складі мережевого графіка

№ п/п	Найменування робіт	Код робіт	Протяжність, год
1	Отримання заявки на перевезення вантажів від клієнтури	1 - 2	7
2	Визначення корреспонудучих точок і відстаней між ними	2 - 3	3
3	Визначення обсягів перевезення	2 - 4	4
4	Вибір рухомого складу для здійснення перевезення	4 - 5	2
5	Фіктивна робота (залежність)	5 - 6	0
6	Розробка раціональних маршрутів перевезень	6 - 7	1,5
7	Розрахунок потрібного парку рухомого складу	7 - 8	2
8	Складання маршрутних відомостей (рознарядки)	8 - 9	4
9	Виписка шляхових листів	9 - 10	3
10	Доставка вантажів споживачам	10 - 11	8
11	Контроль за роботою рухомого складу на лінії	10 - 13	8
12	Прийом товарно-транспортних документів	11 - 12	1,5
13	Обробка товарно- транспортних документів	12 - 14	2
14	Складання диспетчерського звіту	14 - 15	2

Примітка: протяжність робіт вибрана умовно.

2. Побудова мережевого графіка. При цьому користується основними правилами побудови мережевих графіків, а також враховуємо, що взаємопов'язані роботи виконуються послідовно, незалежні роботи виконуються як послідовно, так і паралельно. Будуємо мережевий графік змінно-добового плану перевезення вантажів (див. рис. 6.6.).

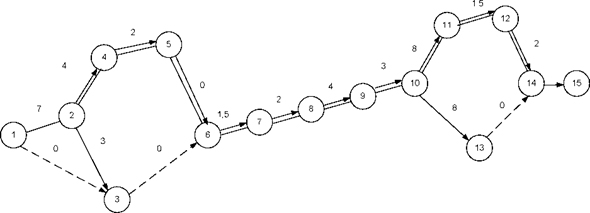
Рисунок – 6.6. Мережевий графік змінно - добового плану перевезення
вантажів

При побудові мережевого графіка використані наступні основні правила:

1. Події позначають кружечками, всередині ставиться номер події (виділяються початкова, кінцеве і проміжні події).

2. Події з'єднуються орієнтованої стрілкою, яка спрямована від попереднього події до подальшого (стрілка показує на мережевому графіку роботу).

3. Будь-які дві події можуть бути з'єднані не більше ніж однією стрілкою.

4. У початкова подія не входить жодна стрілка.

5. З кінцевого події не виходить жодна стрілка.

6. Події мережевого графіка нумеруються так, щоб для кожної роботи номер початкового події був менше, ніж номер кінцевого.

7. Кожну роботу кодують двома цифрами. Перша цифра означає початок роботи та відповідає номеру попереднього події.

8. Тривалість роботи проставляється над стрілками.

9. Частина робіт виконується послідовно (6 - 7), (7 - 8), (8 - 9) і т.д. Це означає, що початок наступної роботи залежить від закінчення попередньої.

10. Роботи (10 - 11), (10 - 13) можуть починатися в один і той же момент часу з настанням події 10. Ці роботи не залежить у часі одна від іншої і можуть виконуватися паралельно.

11. Фіктивні роботи (1 - 3), (3 - 6) і т.д. встановлюють логічний взаємозв'язок і тривалість їх дорівнює 0.

12. Весь комплекс робіт завершується, як тільки закінчиться робота (14 - 15) і здійсниться подія 15.

Складання мережного графіка змінно-добового плану перевезень цим вважається закінченим.

При розробці мережевих графіків необхідно враховувати наступні умови:

1. Ні одна умова не може відбутися доти, поки не будуть включені всі вхідні в нього роботи.

2. Жодна робота, що виходить з даної події, не може початися доти, поки дані подія не відбудеться.

На мережевому графіку видається критичний шлях для подальшої його мінімізації. Для чого визначають час початку і закінчення кожної операції, час настання кожної події, а також встановлюють можливість зміни цих параметрів з метою оптимізації мережевої моделі.

6.4 Розрахунок параметрів мережевої моделі

Розрахунок параметрів мережевої моделі ведеться для повних шляхів, подій і робіт. При розрахунках визначають наступні параметри:

- А) для повних шляхів мережного графіка:

- t (Li) - тривалість будь-якого повного шляху;

- t (Lкр) - тривалість критичного шляху;

- R-(Li) - повний резерв часу шляху.

- Б) для подій:

- T_i^(p), T_i⁽ⁿ⁾ - ранній і пізній терміни здійснення події;

- Ri, - резерв часу події.

- В) для робіт:

- t_ij^(рз), t_ij^(рз) - ранній термін початку та закінчення робіт;

- t_ij^(пп), t_ij^(пз) - пізній термін початку та закінчення робіт;

- r_ij^(п) , r_ij^(B) - повний і вільний резерв часу роботи.

При розрахунку цих параметрів використовують графічний і табличний методи.

6.4.1 Розрахунок тривалості повного шляху

1) Розрахунок тривалості будь-якого повного шляху здійснюється за формулою

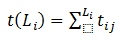(6.1)

Розрахунок зведемо таблицю 6.2.

Таблиця 6.2 –Розрахунок тривалості повного шляху

№ п/п	Шлях, Li	Протяжність шляху, t(Li)	Резерв, R(Li)	Примітка
1	1 - 2 - 4 - 5 - 6 - 7 - 8 - 9 - 10 - 11 - 12 - 14 - 15	7 + 4 + 2 + 0 + 1,5 + 2 + 4 + 3 + 8 + 1,5 + 2 + 2 = 37	0	Критичний шлях
2	1 - 2 - 4 - 5 - 6 - 2 - 8 - 9 - 10 - 13 - 14 - 15	7 + 4 + 2 + 0 + 1,5 + 2 + 4 + 3 + 8 + 0 + 2 = 33,5	3,5
3	1 - 2 - 3 - 6 - 7 - 8 - 9 - 10 - 11 - 12 - 14 - 15	+ 3 + 0 + 1,5 + 2 + 4 + 3 + + 1,5 + 2 + 2 = 34	3,0
4	1 - 2 - 3 - 6 - 7 - 8 - 9 - 10 - 13 - 14 - 15	+ 3 + 0 + 1,5 + 2 + 4 + 3 + + 0 + 2 = 30,5	4,5
5	- 3 - 6 - 7 - 8 - 9 - 10 - - 12 - 14 - 15	0 + 0 + 1,5 + 2 + 4 + 3 + 8 + 1,5 + 2 + 2 = 24	13,0
6	1 - 3 - 6 - 7 - 8 - 9 - 10 - 13 - 14 - 15	0 + 0 + 1,5 + 2 + 4 + 3 + 8 + 0 + 2 = 20,5	16,5

2)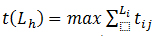 – протяжність критичного шляху (в нашому прикладі це шлях 1).

3) Повний резерв часу шляху

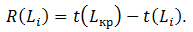(6.2)

Підвищення сумарної тривалості всіх робіт, що лежать на шляху , на величину  не збільшує час настання завершальної операції.

6.4.2 Розрахунок часу настання подій

Розрахунок проведемо на мережевому графіку рис. 6.7.

При графічному методі запису розрахункових параметрів здійснюється безпосередньо на мережевому графіку.

Для чого кожен вузол мережевого графіка ділимо на чотири частини (сектори), в цих секторах записуються такі дані:

• верхній - призначений для запису номера події - i;
• правий - для запису раннього терміну звершення події - T^p_i;
• лівий – для запису пізнього строку здійснення події - T^п_i;
• нижній – для запису резерву часу події - R_i.

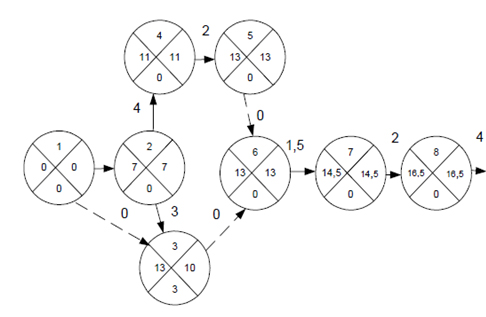
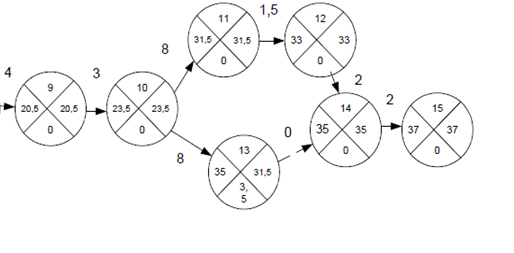
Рисунок 6.7 – Мережевий графік із зазначенням часу настання подій

1. Найбільш ранній термін надходження i-ої події в мережі T^p_i,де i = 1, 2, .. n; i - одна з подій мережі.

T^p_i- мінімально необхідний час між настанням початкової і даної події.

Для початкового події T^p_i = 0 - найбільш ранній термін дорівнює 0. При розрахунку T^p_i послідовно переходять від початкового події до події, все більш від нього віддаленого. Тоді для будь-якого іншої події у цей показник визначається за формулою:

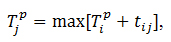(6.3)

де T^(p)_i - найбільш ранній термін надходження події i, що передує події j;

T_ij- Тривалість роботи (i-j).

Для кінцевого події мережного графіка найбільш ранній термін надходження його дорівнює тривалості критичного шляху і називається критичним часом мережевого графіка.

2. Найбільш пізній термін настання події в мережі Tⁿ_i.

Цей показник розраховується від кінця мережевого графіка до початку, тобто в напрямку, зворотному визначенню найбільш раннього терміну настання подій. Для кінцевого події (k) робиться припущення, що найбільш ранній термін його настання дорівнює найбільш пізнього терміну, тобто:

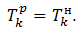(6.4)

Для критичного шляху також вірно рівність:

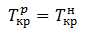(6.5)

Тоді для початкового – Tⁿ₁=0.

Для інших подій мережевого графіка Tⁿ_i визначається за формулою:

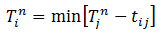(6.6)

де Tⁿ₁ - найбільш пізній термін настання подальшого події j;

t_ij- тривалість роботи (i-j).

Цей показник визначає найбільш допустимий час наступлення події, яке не потребує збільшення часу на здійснення всього комплексу робіт.

Допустимий термін настання події – T^д_i:

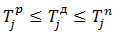(6.7)

Дана нерівність показує, що допустимий термін настання події повинні знаходитися в діапазоні змін від найбільш раннього терміну настання до найбільш пізнього строку настання даної події.

Для критичних подій:

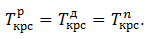(6.8)

3. Резерв часу подій - .

Розрахувавши ранні та пізні терміни настання кожної події, можна визначити резерви часу подій за формулою: .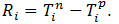

Резерви часу всього критичних подій рівні 0: R_ікр = 0.

6.4.3 Розрахунок часу виконання робіт

Розрахунок часу виконання робіт проводять після того, як визначені  і  для всіх подій:
а) Ранній термін початку робіт () дорівнює раннього терміну наступлення події, з якої виходить дана робота, тобто:

                                                  (6.9)

Якщо цю оцінку виразити через характеристики робіт, то можемо записати:
                                        (6.10)

де  - попередня робота;
 - подальша робота.

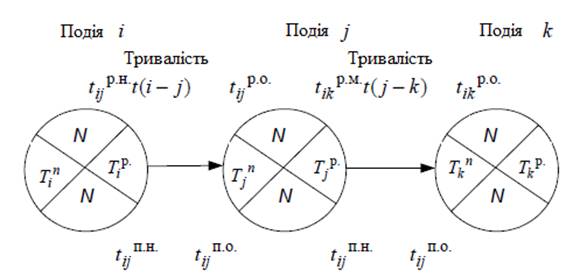
Рисунок 6.4 – Частина мережевого графіка

б) Ранній термін закінчення роботи визначається шляхом додавання до ран-нього терміну початку роботи тривалості самої роботи:

 Або .                         (6.11)
в) Пізній термін закінчення роботи дорівнює пізнього терміну наступлення подальшої події:

 або .                             (6.12)

г) Пізній термін початку роботи перебуває шляхом вирахування з пізнього терміну настання подальшого події тривалості роботи, тобто:

 або .                           (6.13)

д) Повний резерв часу роботи показує час, на який можна перенести початок даної роботи (або збільшити її протяжність), не змінюючи при цьому довжини критичного шляху і визначається за формулами

 або                      (6.14)

Для всіх робіт, що лежать на критичному шляху

.                                              (6.15)

е) Вільний резерв часу роботи - частина повного резерву часу роботи, яка зберігається у неї за умови, що початкова подія роботи сповниться в найпізніший термін, а кінцева - в самий ранній термін і визначається за формулами:

 або .                   (6.16)

Результати розрахунку часових характеристик робіт, мережевого графіка, що розглядається, зведені в табл. 6.3.

6.5 Мережевий графік ремонту автомобілів

Додатково принципи побудови мережевих графіків розглянемо на основі переліку робіт ремонту автомобіля і часу їх виконання (див. табл. 6.4.)
У табл. 6.4. зазначено, що виконання робіт ,  і  може початися тільки після закінчення роботи ; роботи  - після закінчення  і т.д. Встановлення черговості та повного переліку робіт дуже важливе питання при складанні вихідних даних для мережевої моделі та досліджуваного процесу.
Використовуючи дані табл. 6.4, можна побудувати мережевий графік (див. рис. 6.5.), Де роботи зображені векторами (стрілками), а події,що складаються у закінченні робіт і можливості почати нові роботи, - кружками.
Таблиця 6.3 – Таблиця розрахунку часових характеристик мережевого графіка

Щоб відобразити на графіку залежність безпосередньо не опираючихся один на одного робіт, вводиться фіктивна робота, що має нульові витрати часу для її виконання. Вона наноситься на графік пунктирною лінією і потрібна лише для того, щоб зобразити на мережі потребуючу черговість роботи. Наприклад, на рис. 6.5 подію 11 (початок роботи ) можливо тільки тоді, коли будуть виконані роботи  і , звязані через фіктивні роботи (9 - 11) і (10 - 11).
Частина робіт виконується послідовно (2 - 3), (3 - 6), (6 - 9) і т. д. Це означає, що початок кожної наступної роботи залежить від закінчення попередньої.

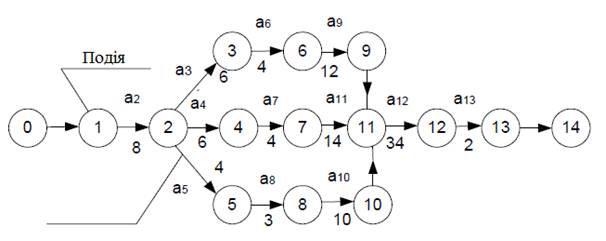
Рисунок 6.5 – Спрощений мережевий графік ремонту автомобіля
Таблиця 6.4 – Перелік робіт ремонту автомобіля і час їх виконання

Роботи (2 - 3), (2 - 4), (2 - 5) можуть починатися в один і той же момент часу з настанням події 2. Ці роботи не залежить у часі ні одна від одної і можуть виконуватися паралельно. Фіктивні роботи (9 - 11), (10 - 11) встановлюють логічний взаємозв'язок, і тривалість їх дорівнює 0. Після побудови мережевого графіка проводиться розрахунок параметрів моделі: тривалість критичного шляху, строків настання подій і часу виконання робіт.
Критичний шлях (critical path) – це послідовність технологічно взаємо-пов'язаних робіт від початкового до кінцевого подій, що має максі-мальную тривалість. Знайдемо критичний шлях для розглянутого прикладу, визначивши, час виконання робіт по кожній з трьох віток:
верхня ()
 = 2 + 8 + 6 + 4 + 12 + 34 + 2 + 0,5 = 68,5 (ч);
середня ()
 = 2 + 8 + 6 + 4 + 14 + 34 + 2 + 0,5 = 70,5 (ч);
нижня ()
 = 2 + 8 + 4 + 3 + 10 + 34 + 2 + 0,5 = 63, 5 (год).
Найбільший час виконання робіт ми отримали на середньої гілки графіка, цей шлях і є критичним:

 (ч).                                      (6.17)

Роботам, лежачим на критичному шляху, приділяється особлива увага, оскільки всяка затримка у виконанні будь-якої з цих робіт призводить до зриву закінчення всього комплексу робіт.
Розрахунок термінів настання подій ведеться в такій послідовності.
Спочатку визначається найбільш ранній термін настання у ¬ ої події в мережі (j), де j = 1, 2, ..., n; n - одна з подій мережі. Для початкової події найбільш ранній термін дорівнює 0, тобто  = 0. Для будь-якого іншої події цей показник визначається за формулою:

(j) = max[(j)+],                                (6.18)

де (i) - найбільш ранній термін настання події i, що передує
i,  - тривалість роботи (i - j) (рис. 6.6.).

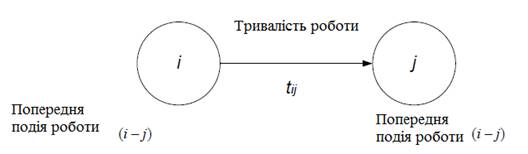
Рисунок 6.6 – Елементи мережевого графіка

Для кінцевого події мережного графіка найбільш ранній термін на ступления дорівнює тривалості критичного шляху.
Найбільш пізній термін настання події в мережі визначається за формулою:
 = min[],                             (6.19)

де  - найбільш пізній термін настання після-дме події j;
 - тривалість роботи i - j.
Цей показник розраховується від кінця мережевого графіка до початку, тобто в напрямку, зворотному визначенню найбільш раннього терміну наступлення подій. Для кінцевого події k робиться припущення, що найбільш ранній термін його настання дорівнює найбільш пізнього терміну, тобто . Для критичних подій мережевого графіка . Для початкового події  = 0.
Допустимий термін настання події .
Дана нерівність показує, що допустимий термін настання події повинен знаходитися в діапазоні змін від найбільш раннього терміну настання до найбільш пізнього допустимого терміну настання даної події. Для критичних подій:

.                               (6.20)

Результати розрахунків термінів настання подій для мережевого графіка, представленого на рис. 6.5, наведено в табл. 6.5.
У рамках мережевого графіка кожна робота характеризується дотримуюся-ські чеирьмя часовими параметрами:
1) Ранній початок роботи - визначається як тривалість шляху найбільшої довжини від початкового події до попередньої події даної роботи. Ранній початок будь-якої подальшої роботи (j-k) 162
дорівнює сумі значень раннього початку і тривалості роботи (i-j),
попередньої для даної роботи (рис. 6.4)

.                                          (6.21)

Ранній початок робіт, що виходять з першої події, дорівнює нулю. Якщо даній роботі передують дві і більша кількість робіт, то її ранній початок дорівнює максимальному значенню сумм раннього початку і тривалості попередньої роботи
Ранній початок роботи j-k рівне найбільш раннього терміну наступлення  попередньої події j, тобто
2) раннє закінчення роботи  визначається як сума раннього початку робіт і її тривалості
3) пізній початок робіт   являє собою найпізніший термін початку роботи, який не викликає затримки виконання всього комплекса в цілому.

Таблиця 6.5 – Результати розрахунків термінів настання подій для мережевого графіка

* Події, що лежать на критичному шляху.
Пізніше початок роботи розраховується в зворотному порядку, від кінця мережевого графіка до початку, і визначається як різниця між про-тривалістю критичного шляху від кінцевого стану графа до попереднього події даної роботи;
4)пізнє закінчення роботи  рівне часу закінчення роботи,
якщо вона була розпочата в пізній термін, і тому визначається як сума, пізнього початку і її тривалості  .
Якщо відомо пізніше закінчення наступної роботи, то для даної роботи значення пізнього закінчення визначиться наступним чином:

.                                         (6.22)

Пізніше закінчення роботи ГПО мережевого графіка завжди рівне найбільш пізньому терміну настання подальшого події , тобто:

.                                          (6.23)

Результати розрахунків часових параметрів робіт зведені в табл. 6.6.
З таблиці. 6.6. випливає, що значення критичного шляху визначається за максимальною величиною їх ранніх закінчень робіт і рівне 70,5.
Пізніше закінчення роботи (13 - 14), що завершується подією 14, дорівнює максимальному значенню їх ранніх закінчень робіт і також визначає тривалість критичного шляху.
Роботи, у яких ранні початку і закінчення відповідно рівні пізнім початком і закінченням, лежать на критичному шляху і не мають
запасів часу. Для даного графіка до цих робіт відносяться (0 - 1), (1
2), (2 - 4), (4 - 7), (7 - 11), (11 - 12), (12 - 13), (13 - 14).

Таблиця 6.6 – Результати розрахунків часових параметрів робіт

Повний (загальний) запас часу , що представляє собою час, на
яке можна перенести початок робіт (i-j) або, навпаки, збільшити їх тривалість без зміни загального терміну виконання комплексу
робіт, і визначений за формулою .

6.6 Поняття оптимізація і переваги мережевих моделей

Після того, як побудований вихідний мережевий графік і розраховані основні параметри мережевої моделі, необхідно дати оцінку отриманим результатам. Якщо критичний шлях більше встановленого терміну, запропонованого керівництвом, то необхідно здійснити оптимізацію мережевого графіка.
Під оптимізацією розуміють процес поліпшення мережевого графіка шляхом:
а) зменшення загального часу виконання робіт критичного шляху (оптимізація за часом);
б) забезпечення виконання всього комплексу робіт при обмежених ре-ресурсах (оптимізація по ресурсах).
Оптимізація мережевого графіка за часом полягає в зменшенні критичного шляху і проводиться в наступному порядку:
1. уточнення часу виконання робіт;
2. скорочення часу виконання критичних робіт за рахунок удосконалення технології їх виробництва;
3. вивчаються можливості заміни послідовно виконуваних робіт паралельними там, де це допускається технологією, з метою зменшення тривалості робіт;
4. перерозподіл ресурсів з некритичних на критичні роботи, виконання останніх у дві або три зміни;
5. скорочуються терміни виконання комплексу робіт за рахунок застосування додаткових ресурсів, а також застосування технологічних умов виробництва комплексу робіт.
Якщо вихідний варіант мережевого графіка має тривалість критичного шляху, відповідну директивному терміну або перевищує цей термін, то він вважається оптимальним і може бути рекомендований до затвердження та виконання.
Оптимізація мережі по ресурсах. Оптимізація мережевого графіка за часом без врахування обмежень по ресурсах передбачає, що потребність в ресурсах може бути встановлена в необхідні терміни. Однак такий підхід до розробки мережевих графіків не виключає вирішення завдання найбільш раціонального розподілу ресурсів, тому після оптимізації мережевої моделі за критерієм «часу» проводиться її оптимізація по ресурсах.
Перевагами мережевих моделей є:
1. Мережеві графіки дають чітке уявлення про загальний обсяг робіт комплексу.
2. Забезпечують наочність технологічної послідовності робіт.
3. Мережеві моделі забезпечують розподіл коштів і робочої сили, що створює умови для найкращого використання ресурсів.
4. Дозволяють здійснювати поточне планування виконання робіт, прогнозувати складні процеси, виявляти «вузькі місця» виробництва.
5. Скоротити втрати часу при виконанні всього комплексу робіт.
6. Вибрати оптимальний варіант виконання робіт.

Контрольні запитання

1. Призначення мережевого планування.
2. Елементи мережевих графіків і їх відображення на мережевий моделі.
3. Що таке «критичний шлях»?
4. Перерахуйте основні правила побудови мережевих графіків.
5. Перерахуйте етапи побудови мережевих графіків.
6. Параметри мережевих моделей для повного шляхи і способи їх обчислення.
7. Параметри мережевих моделей для подій і способи їх обчислення.
8. Параметри мережевих моделей для робіт і способи їх обчислення.
9. Допустимий термін настання події та резерв часу події.
10. Повний і вільний резерв часу роботи і способи їх обчислення.
11. Сутність оптимізації мережевого графіка за часом і за ресурсам.
12. Переваги мережевих моделей.

 

---