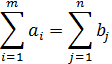7 МЕТОДИ ЛІНІЙНОГО ПРОГРАМУВАННЯ
7.1 Загальні положення
При вирішенні широкого кола завдань автомобільного транспорту використовуються методи лінійного програмування (method of linear programming). Лінійне програмування метод розв'язання екстремальних задач, в яких: 1) Показник ефективності W - представляє лінійну функцію від змінних ![]() ,
, ![]() , ...,
, ..., ![]() .
.
![]() (7.1)
(7.1)
Обмеження являють собою систему лінійних рівнянь або нерівність виду
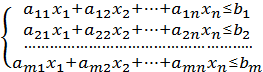 (7.2)
(7.2)
де i=1,2,…,m; j=1,2,…, n; ![]() .
.
У випадку завдання лінійного програмування (ЗЛП) формулюється таким чином: знайти величини ![]() ,
, ![]() , ...,
, ..., ![]() , при яких цільова функція (8.1) досягає максимуму (мінімуму), і задовольняє обмеженням, які являють собою систему лінійних рівнянь або нерівностей виду (7.2.).
, при яких цільова функція (8.1) досягає максимуму (мінімуму), і задовольняє обмеженням, які являють собою систему лінійних рівнянь або нерівностей виду (7.2.).
Задачі лінійного програмування мають декілька форм запису:
1) Векторна форма запису: ![]() .
.
При обмеженнях
![]() , (7.3)
, (7.3)
![]() ;
;
де ![]() ;
;
![]() – скалярна похідна.
– скалярна похідна.
Вектори ![]() ;
; ![]() ;….
;…. ![]() ,
, 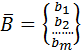 - складають відповідно з коефіцієнтів при невідомих і вільних членах.
- складають відповідно з коефіцієнтів при невідомих і вільних членах.
2) Матрична форма запису:
![]() . (7.4)
. (7.4)
При обмеженнях ![]() ,
,
де ![]() - матриця –строка;
- матриця –строка;
![]() - матриця-стовбець;
- матриця-стовбець;
![]() - матриця системи =
- матриця системи = 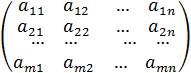 ;
;
CX і AX – похідні матриць;
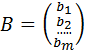 - матриця-стовбець.
- матриця-стовбець.
3) Запис за допомогою знаків підсумовування:
![]() (7.5)
(7.5)
при обмеженнях ![]() .
.
Система рівнянь (8.2) визначає область вирішення ОДР.
Зобразимо область рішень ОДР для двовимірного випадку, тобто (![]() і
і ![]() ) на площині (див. рис. 7.1.), тоді:
) на площині (див. рис. 7.1.), тоді:
1) Б1, Б2, Б3, Б4, Б5, Б1 - область вирішення ОДР.
2) А1, Б2, Б3, А2, 0, Ф1 - область допустимих рішень, тому що ![]() .
.
3) Вершини багатокутника, для яких ![]() , А1, Б2, Б3, А2 називаються опорними точками.
, А1, Б2, Б3, А2 називаються опорними точками.
4) Значення цільової функції в опорних точках називають опорними рішеннями.
5) В одній з вершин 0, А2, Б2, Б3, А2 ![]() , які називають оптимальним рішенням, тобто тільки в одній точці можемо мати оптимальне рішення.
, які називають оптимальним рішенням, тобто тільки в одній точці можемо мати оптимальне рішення.
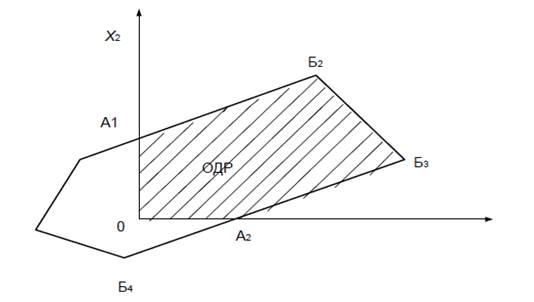
ОДР – область допустимих рішень
Рисунок 7.1 – Область рішень ЗЛП для двовимірного випадку
7.2 Двоїста задача лінійного програмування
Кожна задача лінійного програмування, що задається системою лінійних нерівностей з невід'ємними змінними, може мати форму прямої задачі та завдання, двоїстої до неї. Нехай маємо пряму задачу (вихідну).
Знайти значення ![]() і мінімум цільової функції W(x) при обмеженнях.
і мінімум цільової функції W(x) при обмеженнях.
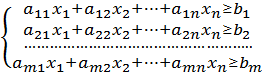 (7.6)
(7.6)
де ![]() .
.
Двоїста задача до вихідної (прямої) задачі виходить, якщо:
1) транспонувати матрицю коефіцієнтів системи обмежень;
2) поміняти ролями вільні члени системи обмежень і коефіцієнти цільової функції;
3) змінити напрямки нерівностей;
4) в цільовій функції замінити min і max.
Двоїста задача запишеться так. Знайти значення ![]() і максимум цільової функції Z(y) за умови:
і максимум цільової функції Z(y) за умови:
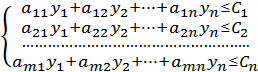 (7.7)
(7.7)
де ![]() .
.
Примітка. 1) Двоїста задача до двоїстої – є пряме завдання. 2) Перехід до двоїстої завданню дозволяє скоротити обсяги розрахунків. 3) За рішенням однієї з двоїстих завдань знаходиться оптимальне рішення іншої, що підтверджується теорією двоїстості.
Теорема (двоїстості). Якщо з пари двоїстих задач одна має оптимальним рішенням, то й інша має рішення, причому для екстремальних значень цільової функції виконується співвідношення:
![]() . (7.8)
. (7.8)
Приклад. Нехай маємо вихідну задачу лінійного програмування
![]()
при обмеженнях
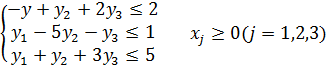 (7.9)
(7.9)
Потрібно записати двоїсту задачу. Розв’язок.
![]() (7.10)
(7.10)
при обмеженнях
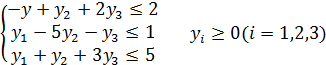 (7.11)
(7.11)
7.3 Формулювання задачі лінійного програмування
У загальному вигляді завдання можна сформулювати так: підприємство може виготовити вироби двох видів ![]() і
і ![]() . Для з-товлення цих виробів необхідно мати три види сировини
. Для з-товлення цих виробів необхідно мати три види сировини ![]() ,
, ![]() і
і ![]() , ресурси яких обмежені. На виробництво одного виробу потрібно певну кількість сировини, для конкретного випадку вони представле-ни табл. 7.1. У цій таблиці також наведені доходи від реалізації від одного виробу в умовних одиницях.
, ресурси яких обмежені. На виробництво одного виробу потрібно певну кількість сировини, для конкретного випадку вони представле-ни табл. 7.1. У цій таблиці також наведені доходи від реалізації від одного виробу в умовних одиницях.
Потрібно визначити, скільки і яких видів виробів треба виробляти, щоб дохід підприємства був максимальним.
Таблица 1.1 – Запас сировини для виробництва одного виробу
Вид сировини |
Вид продукції |
Запас cировини ( |
|
|
|
||
|
|
|
28 |
|
|
|
10 |
|
|
|
24 |
Дохід від одного виду продукції |
|
|
|
Кількістьо одиниць продукції |
|
|
|
Використовуючи дані табл. 8.1, запишемо цільову функцію нашої задачі.
![]() (7.12)
(7.12)
де ![]() ,
, ![]() – вартість виробів;
– вартість виробів;
![]() ,
, ![]() – кількість виробів.
– кількість виробів.
Система обмежень запишеться так:
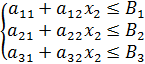 ; (7.13)
; (7.13)
Або
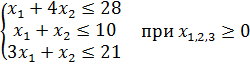 . (7.14)
. (7.14)
Отже, задача лінійного програмування (ЗЛП) сформульована у словесній і математичній формі.
ЗЛП має кілька методів рішення. Ми розглянемо графіче ¬ ський метод і метод симплексних таблиць.
7.4 Геометрична інтерпретація задачі лінійного програмування
Оскільки в задачі тільки дві змінні, а умови для них записани у вигляді нерівностей першого ступеня, можна розглянути геометричну інтерпретацію завдання у площині координат ![]() ,
,![]() .
.
Умови (7.5), що накладаються на змінні ![]() ,
, ![]() означають, що область допустимих значень
означають, що область допустимих значень ![]() ,
, ![]() для кожної умови лежить в заштрихованій напівплощині (рис. 7.2).
для кожної умови лежить в заштрихованій напівплощині (рис. 7.2).
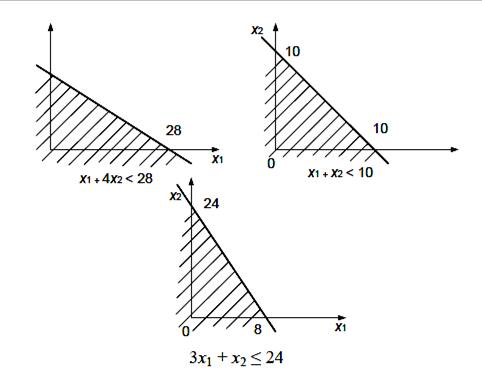
Рисунок 7.2 – Область допустимих значень ![]() ,
, ![]() для кожної умови лежить в заштрихованій напівплощині
для кожної умови лежить в заштрихованій напівплощині
Область зміни ![]() ,
,![]() , задовольняє всім трьом умовам, лежить в опуклому багатокутнику 0
, задовольняє всім трьом умовам, лежить в опуклому багатокутнику 0![]()
![]()
![]()
![]() з вершинами 0 (0, 0),
з вершинами 0 (0, 0), ![]() (0; 7),
(0; 7), ![]() (6, 4),
(6, 4), ![]() (7, 3) ,
(7, 3) , ![]() (8; 0) (рис. 7.3).
(8; 0) (рис. 7.3).
Розглянемо тепер лінії рівня функції W (![]() ,
,![]() ), сімейство паралельних прямих 3
), сімейство паралельних прямих 3![]() + 2
+ 2![]() = С.
= С.
Для W (![]() ,
,![]() ) = 0 лінія пройде через початок координат. Для більших C лінії рівня розташовані правіше. Отже, максимум функції W (
) = 0 лінія пройде через початок координат. Для більших C лінії рівня розташовані правіше. Отже, максимум функції W (![]() ,
,![]() ) = 3
) = 3![]() + 2
+ 2![]() реалізується в точці (
реалізується в точці (![]() ,
,![]() ), що лежить на лінії рівня функції W (
), що лежить на лінії рівня функції W (![]() ,
,![]() ) = С, яка розташована на найбільшій відстані від нуля вправо. З іншого боку, ми шукаємо найбільше значення W (
) = С, яка розташована на найбільшій відстані від нуля вправо. З іншого боку, ми шукаємо найбільше значення W (![]() ,
,![]() ) в області зміни змінних 0
) в області зміни змінних 0 ![]()
![]()
![]() . Отже, оптимальне рішення лежить на лінії рівня 3
. Отже, оптимальне рішення лежить на лінії рівня 3![]() + 2
+ 2![]() = С, що перетинає область 0
= С, що перетинає область 0 ![]()
![]()
![]() в точці
в точці ![]() . Таким чином, точка
. Таким чином, точка ![]() (7, 3) є точкою оптимального рішення з координатами Ж (х1, х2) = 3-7 + 2-3 = 27.
(7, 3) є точкою оптимального рішення з координатами Ж (х1, х2) = 3-7 + 2-3 = 27.
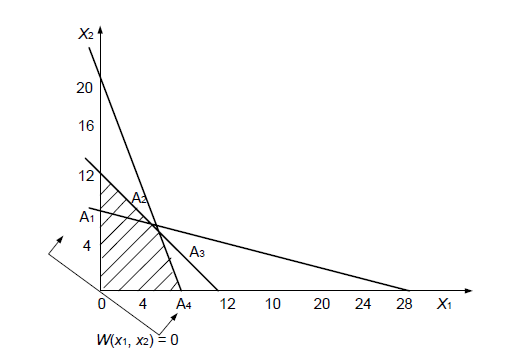
Рисунок 7.3 – Область зміни ![]() ,
,![]() , задовольняє всім трьом умовам, лежить в опуклому багатокутнику 0
, задовольняє всім трьом умовам, лежить в опуклому багатокутнику 0![]()
![]()
![]()
![]()
7.5 Симплексний метод розв'язку задач
Нехай потрібно знайти max (min) цільової функції:
![]() (7.15)
(7.15)
при обмеженнях
![]() , (7.16)
, (7.16)
де ![]() ;
; ![]() ,
, ![]() ,
, ![]() – постійні величини (коефіцієнти), тобто маємо ЗЛП.
– постійні величини (коефіцієнти), тобто маємо ЗЛП.
Для вирішення ЗЛП застосовують різні числові методи. Одним з найбільш поширених (універсальних) методів є сім-комплексний метод (табличний).
Для вирішення ЗЛП симплекс-методом попередньо необхідно провести наступні перетворення:
1) Рівняння системи обмежень (7.2) записати в канонічному вигляді, для чого замінюємо нерівності (7.2) равенствами шляхом введення додаткових невід'ємних змінних. Одержуємо:
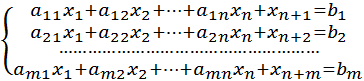 (7.17)
(7.17)
де ![]() ,
, ![]() , ... ,
, ... , ![]() - деякі нові невід'ємні змінні, які називають додатковими (фіктивними).
- деякі нові невід'ємні змінні, які називають додатковими (фіктивними).
2) Додаткові змінні можна ввести і в цільову функцію з нульовими коефіцієнтами. Тоді отримаємо:
![]() (7.18)
(7.18)
Примітка: 1) запис ЗЛП у вигляді рівнянь 8.6 і 8.7 називають канонічною;
2) додаткові змінні ![]() і т.д. позитивні, як і
і т.д. позитивні, як і ![]() , ...
, ... ![]() ; загальна кількість змінних буде
; загальна кількість змінних буде ![]() , де n - початкові, m - додаткові (дорівнює числу рівнянь); 4) завжди можливий зворотний перехід.
, де n - початкові, m - додаткові (дорівнює числу рівнянь); 4) завжди можливий зворотний перехід.
На перший погляд перехід ЗЛП до канонічного виду ускладнює задачу, але виявляється, що це дозволяє більш ефективно провести дослідження завдання на оптимальність.
7.5.1 Основні положення методу
Наведемо рівняння (8.4), (8.5) до канонічної формі. Для цього введемо додаткові змінні ![]() ,
, ![]() ,
, ![]() і запишемо задачу у вигляді:
і запишемо задачу у вигляді:
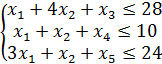 (7.19)
(7.19)
де ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
W = 3![]() + 2
+ 2![]() + 0
+ 0![]() + 0
+ 0![]() + 0
+ 0![]() (7.20)
(7.20)
Слід знайти ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , які задовольняють умовам (7.8) забезпечують максимум цільової функції W (
, які задовольняють умовам (7.8) забезпечують максимум цільової функції W (![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ).
).
Пошук оптимального рішення почнемо з вибору значень, удовле-яка творить умовам (7.8). Найлегше це зробити для ![]() =
= ![]() = 0, тоді
= 0, тоді ![]() = 28,
= 28, ![]() = 10,
= 10, ![]() = 24. Таке початкове наближення оптимального рішення назвемо опорним рішенням:
= 24. Таке початкове наближення оптимального рішення назвемо опорним рішенням: ![]() = 0,
= 0, ![]() = 0,
= 0, ![]() = 28,
= 28, ![]() = 10,
= 10, ![]() = 24.
= 24.
Йому відповідає значення цільової функції ![]() = 0.
= 0.
Визначимо з умови (7.8) ненульові змінні ![]() ,
, ![]() ,
, ![]() (назвемо їх базисними змінними) через
(назвемо їх базисними змінними) через ![]() ,
, ![]() (назвемо їх вільними):
(назвемо їх вільними):
![]() = 28 -
= 28 - ![]() - 4
- 4![]() ,
,
![]() = 10
= 10![]() -
- ![]() , (7.21)
, (7.21)
![]() = 24 - 3
= 24 - 3![]() -
- ![]() .
.
Цільова функція в змінних ![]() ,
, ![]() така: W (
така: W (![]() ) = 3
) = 3![]() + 2
+ 2![]() . Видно, що збільшуючи
. Видно, що збільшуючи ![]() ,
, ![]() , можна збільшити значення цільової функції. Нехай, наприклад,
, можна збільшити значення цільової функції. Нехай, наприклад, ![]() = 0. Тоді максимально допустиме значення
= 0. Тоді максимально допустиме значення ![]() = 8 (див.
= 8 (див.
рис. 8.3). Отримаємо нове опорне рішення ![]() = 8,
= 8, ![]() = 0,
= 0, ![]() = 20,
= 20, ![]() = 2,
= 2, ![]() = 0. Йому відповідає значення цільової функція
= 0. Йому відповідає значення цільової функція
![]() = 24>
= 24>![]() Отже, друге опорне рішення найкраще.
Отже, друге опорне рішення найкраще.
Приймемо тепер нульові змінні (![]() і
і ![]() ) за вільні, а решта (
) за вільні, а решта (![]() ,
, ![]() ,
, ![]() ) - за базисні. Із системи (8.8) отримаємо:
) - за базисні. Із системи (8.8) отримаємо:
![]() = 8 - (1/3)
= 8 - (1/3) ![]() - (1/3)
- (1/3) ![]() ,
,
![]() = 20 - (10/3)
= 20 - (10/3) ![]() + (1/3)
+ (1/3) ![]() , (7.22)
, (7.22)
![]() = 2 - (2/3)
= 2 - (2/3) ![]() + (1/3)
+ (1/3) ![]() .
.
У нових вільних змінних цільова функція має вигляд:
W = 24 + ![]() -
- ![]() . (7.23)
. (7.23)
Таким чином, для збільшення цільової функція W потрібно збільшити значення вільної змінної ![]() , залишаючи
, залишаючи ![]() = 0. З формули (7.10) видно, що найбільше допустиме значення
= 0. З формули (7.10) видно, що найбільше допустиме значення ![]() = 3. Тоді нове опорне рішення таке:
= 3. Тоді нове опорне рішення таке:
![]() = 7,
= 7, ![]() = 3,
= 3, ![]() = 10,
= 10, ![]() = 0,
= 0, ![]() = 0, а значення цільової функції
= 0, а значення цільової функції ![]() = 3*7 + 2*3 = 27>
= 3*7 + 2*3 = 27> ![]() .
.
Як і колись за вільні змінні виберемо ![]() і
і ![]() , а за базисні -
, а за базисні - ![]() ,
, ![]() і
і ![]() . Із системи (7.8) отримаємо:
. Із системи (7.8) отримаємо:
![]() = 7 +
= 7 + ![]() /2 -
/2 - ![]() /2,
/2,
![]() = 3 - 3
= 3 - 3![]() /2 +
/2 + ![]() /2, (7.24)
/2, (7.24)
![]() = 9 - 11
= 9 - 11![]() /2 - 3
/2 - 3![]() /2.
/2.
Цільова функція має вигляд W = 27 - (3/2) ![]() - (1/5)
- (1/5) ![]() . Видно, що не можна змінити значення
. Видно, що не можна змінити значення ![]() і
і ![]() , що не зменшивши значення цільової функції. Отже, останнє опорне рішення оптимально. Як і при вирішенні завдання геометричним способом, отримано оптимальне рішення
, що не зменшивши значення цільової функції. Отже, останнє опорне рішення оптимально. Як і при вирішенні завдання геометричним способом, отримано оптимальне рішення ![]() = 7,
= 7,
![]() = 3, що дає максимальне значення функції
= 3, що дає максимальне значення функції
W (![]() ,
, ![]() ) = 3
) = 3![]() + 2
+ 2![]() (7.25)
(7.25)
![]() = 7,
= 7, ![]() = 3.
= 3.
Описаний метод рішення - симплекс - метод полягає в побудові послідовності опорних рішень, що збільшують цільову функцію.
Зобразимо опорні рішення в площині ![]() ,
, ![]() , позначаючи точки цифрою, що відповідає номеру опорного рішення (рис. 8.4).
, позначаючи точки цифрою, що відповідає номеру опорного рішення (рис. 8.4).
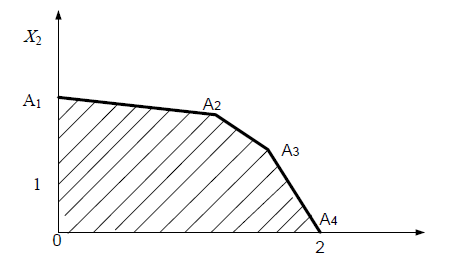
Рисунок 7.4 – Опорні рішення в площині ![]() ,
, ![]()
Таким чином ми будуємо опорні рішення симплекс-методом, пе-реходу від початку координат до оптимального рішення по периметру багатокутники 0 ![]()
![]()
![]()
![]() , який був отриманий при вирішенні завдання геометричним способом.
, який був отриманий при вирішенні завдання геометричним способом.
З опису методу на прикладі видно, що алгоритм симплекс-методу носить ітераційний характер. Один крок методу полягає в побудові чергового опорного рішення.
7.5.2 Алгоритм методу
Опишемо алгоритм симплекс-методу для загальної канонічної задачі лі-лінійного програмування (8.6), (8.7). Допустимим рішенням назвемо всяке рішення системи (8.6), що задовольняє умові ![]() . Допустиме рішення, на якому цільова функція (8.7) приймає максимальне значення, назвемо оптимальним.
. Допустиме рішення, на якому цільова функція (8.7) приймає максимальне значення, назвемо оптимальним.
Залежно від матриці системи (8.6) можливі наступні випадки:
1) Система (7.6) не має рішень, тобто несумісна. У цьому випадку завдання лінійного програмування не можна розв'язати.
2) Система (7.6) не має допустимих рішень, а значить, завдання нелінійного програмування не має рішення.
3) Система (7.6) має єдине допустиме рішення. У цьому випадку єдине рішення системи (7.6) є оптимальним.
4) Система (7.6) має нескінченну безліч допустимих рішень, але цільова функція не обмежена на цій множині допустимих рішень, а, значить, завдання лінійного програмування не розв'язна.
5) Система (7.6) має безліч допустимих рішень, і цільова функція обмежена на безлічі допустимих рішень. У цьому випадку завдання лінійного програмування має оптимальне рішення. Будемо надалі вважати, що завдання (7.6), (7.7) має оптимальне рішення.
Симплекс-метод полягає в послідовному побудові таких опорних рі-шень, що кожне наступне збільшує цільову функцію і максимум досягається за кінцеве число кроків.
Узагальнений алгоритм симплексного методу розв'язання ЗЛП наведено на рис. 7.5 і включає наступну послідовність операцій:
1) Рівняння системи обмежень запишемо в канонічному вигляді. Для цього: а) замінимо нерівності равенствами шляхом введення додаткових (фіктивних) змінних; б) добиваємося, щоб всі вільні члени системи обмежень були позитивними.
2) Знаходимо перший опорне рішення. Для цього: а) всі змінні п розбиваємо на m-базисних і k=n-m-вільних; б) в якості базисних змінних вибираємо додаткові змінні; в) вважаючи, що всі вільні змінні дорівнюють нулю отримаємо перше опорне рішення.
3) За правилами 1, 2 визначаємо оптимальність прийнятого рішення.
4) За відсутності оптимальності за певним правилом видаляємо з базисних змінних одну і вводимо іншу з числа вільних.
5) Проводимо повторну перевірку на оптимальність.
Примітка. Для впорядкування переходу від одного опорного рішення користуємося ітераційними таблицями. Ітераційні таблиці, складання за нижченаведеними правилами, дозволяють здійснювати перехід від гіршого рішення тільки на краще, до отримання оптимального рішення.
7.6 Оптимізація вантажопотоків
Завдання оптимізації вантажопотоків вирішуються методами лінійного програмування, які дозволяють встановити оптимальне закріплення споживачів вантажу за постачальниками, вибрати маршрути перевезень вантажів, вирішити питання розподілу парку рухомого складу по АТП і т.д.
В якості критеріїв оптимальності беруть пробіг рухомого складу, час доставки вантажу, грошові або трудові витрати.
7.6.1 Формулювання «транспортної задачі»
Окремим випадком задачі лінійного програмування є «транспортне завдання», яка формулюється так: Мається m постачальників (![]() ,
, ![]() , ...,
, ..., ![]() ), які розташовують запасами однорідного вантажу (Г) - (
), які розташовують запасами однорідного вантажу (Г) - (![]() ,
, ![]() , ...,
, ..., ![]() ), а також є n споживачів (
), а також є n споживачів (![]() ,
, ![]() , .. ..,
, .. .., ![]() ), яким необхідно завести (
), яким необхідно завести (![]() ,
, ![]() , ...,
, ..., ![]() ) тон вантажу, а також відомі відстані між грузопунктами.
) тон вантажу, а також відомі відстані між грузопунктами.
Необхідно так закріпити постачальників за споживачами, щоб затрати на перевезення були min (тобто min транспортної роботи).
Вихідні дані «транспортної» задачі представляють звичайно у вигляді таблиці 7.5. Математична модель транспортної задачі в загальному вигляді записується в наступній формі. Дана цільова функція
![]()
і обмеження
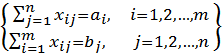 (7.26)
(7.26)
Необхідно знайти такі невід'ємні значення змінних ![]() , що задовольняють обмеженням, а цільова функція при цьому досягає мінімуму.
, що задовольняють обмеженням, а цільова функція при цьому досягає мінімуму.
При вирішенні задачі оптимального закріплення споживачів вантажу за постачальниками символіці виразів (7.11) і (7.12) можна надати наступний фізичний зміст:
m - кількість постачальників;
n - кількість споживачів;
![]() - кількість вантажу, що відправляється i-им постачальником;
- кількість вантажу, що відправляється i-им постачальником;
![]() - кількість вантажу, що доставляється j-му споживачеві;
- кількість вантажу, що доставляється j-му споживачеві;
![]() - кількість вантажу, що доставляється від i-го постачальника j-му споживачеві.
- кількість вантажу, що доставляється від i-го постачальника j-му споживачеві.
![]() - відстань між i-им і j-им пунктами.
- відстань між i-им і j-им пунктами.
Таблица 7.5 – Вихідні дані «транспортної» задачі
Пункти Відправлення |
Пункти призначення |
Запаси |
|||
|
|
… |
|
||
|
|
|
… |
|
|
|
|
|
… |
|
|
… |
… |
… |
… |
… |
… |
|
|
|
… |
|
|
Потребності |
|
|
… |
|
|
7.6.2 Послідовність розв’язку транспортної задачі
У рішенні транспортної задачі виділяють три етапи:
1. Визначення початкового плану перевезень.
2. Перевірка отриманого плану на оптимальність.
3. Перехід до нового плану перевезень з перевіркою на оптимальність.
Перший етап. Початковий план перевезень прийнято встановлювати методом північно-західного кута або методом найменшої вартості.
Метод північно-західного кута полягає в тому, що спочатку повністю задовольняються потреби першого споживача (якщо це можливо) за рахунок першого постачальника, залишок передається другому споживачу і т.д. Одночасно потрібно стежити потім, щоб дотримувався баланс по рядках і стовпцях. Цей метод дозволяє легко знайти початковий план перевезень, але він, як правило, далекий від оптимального.
Метод найменшої вартості передбачає першочергове за-конання тих клітин, які розташовують найменшою відстанню перевезень (найменшою вартістю). При цьому план перевезень, як правило, буде ближче до оптимального.
Другий етап. Перевірка початкового плану на оптимальність може здійснюватися різними методами. Найбільш поширеним є метод потенціалів. Відповідно до даного методу для отримання оптимального плану перевезень ![]() необхідно і достатньо введення допоміжних чисел (
необхідно і достатньо введення допоміжних чисел (![]() , i = 1, 2, .., m і
, i = 1, 2, .., m і ![]() , j= 1, 2, ..., n, званих потенціалами, при яких виконувалися б умови:
, j= 1, 2, ..., n, званих потенціалами, при яких виконувалися б умови:
![]() (7.27)
(7.27)
![]() (7.28)
(7.28)
де ![]() - потенціал j-го стовпця,
- потенціал j-го стовпця, ![]() - потенціал i-го рядка.
- потенціал i-го рядка.
Умова (8.13) має дотримуватися для зайнятих клітин таблиці, а умова (8.14) - для вільних. Якщо умова оптимальності (12) не дотримується хоча б для однієї клітки, це означає, що отриманий план перевозок не є оптимальним і потрібно шукати інший.
Третій етап іирішення транспортної задачі (одержання нового плану перевезень) розглянемо на конкретному прикладі.
7.6.3 Приклад розв’язку задачі
Приклад. Знайти оптимальний план перевезень вантажів. Запаси на складах, потреби пунктів призначення і відстані перевезень однорідного вантажу по пунктах призначення вказані в табл. 8.6.
Розв’язок. Складаємо початковий план перевезень методом північно-західного кута (табл. 8.7). Визначаємо потенціали за стовпцями рядках для зайнятих клітин по умові (8.13). Один з потенціалов ![]() вибираємо довільно. Наприклад
вибираємо довільно. Наприклад ![]() = 0.
= 0.
Тоді для клітини ![]()
![]() згідно з умовою
згідно з умовою ![]() , маємо
, маємо ![]() , якщо раніше прийнято
, якщо раніше прийнято ![]() = 0, то
= 0, то ![]() = 4.
= 4.
Для клітин ![]()
![]()
![]() +
+ ![]() = 5 при
= 5 при ![]() = 0,
= 0, ![]() = 5;
= 5;
![]()
![]()
![]() +
+ ![]() = 10 при
= 10 при ![]() - 5,
- 5, ![]() - 5;
- 5;
![]()
![]()
![]() +
+ ![]() = 5 при
= 5 при ![]() - 5,
- 5, ![]() - 0;
- 0;
![]()
![]()
![]() +
+ ![]() = 8 при
= 8 при ![]() - 8,
- 8, ![]() - 0;
- 0;
![]()
![]()
![]() +
+ ![]() = 6 при
= 6 при ![]() - 6,
- 6, ![]() - 0.
- 0.
Отримані значення потенціалів проставляємо у допоміжні рядки і стовпці розрахункової табл. 7.7.
Таблиця 7.6 – Значення потенціалів
Пункти відправлення |
Пункти призначення і відстані перевезень |
Запаси |
|||
|
|
|
|
||
|
4 |
8 |
3 |
12 |
100 |
|
5 |
10 |
4 |
18 |
80 |
|
7 |
5 |
8 |
6 |
240 |
Потребності |
160 |
90 |
120 |
50 |
420 |
Таблиця 7.7 – Початковий план перевезень методом північно-західного кута
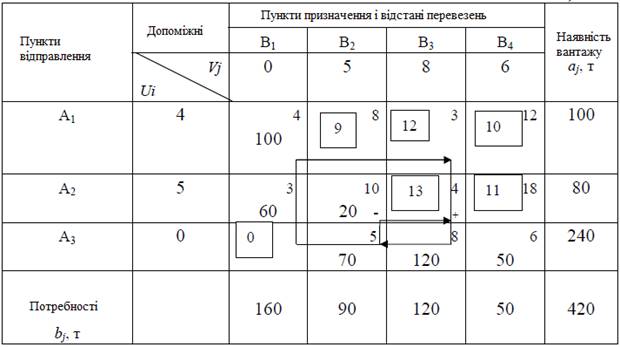
Вільні клітки, для яких ![]() = 0, перевіряємо на виконання умови (12), для чого значення суми потенціалів (
= 0, перевіряємо на виконання умови (12), для чого значення суми потенціалів (![]() +
+ ![]() ) для даних клітин проставляємо у верхні ліві кути вільних клітин табл. 7.7 і перевіряємо всі ці клітини на виконання умови
) для даних клітин проставляємо у верхні ліві кути вільних клітин табл. 7.7 і перевіряємо всі ці клітини на виконання умови ![]() +
+ ![]()
![]() .
.
Порівнянням встановлюємо, що для клітин ![]()
![]() ,
, ![]() і
і ![]()
![]() умова (12) не виконується, так як відповідно: 5 + 4 = 9> 8, 8 + 4 = 12> 3, 8 + 5 = 13> 4.
умова (12) не виконується, так як відповідно: 5 + 4 = 9> 8, 8 + 4 = 12> 3, 8 + 5 = 13> 4.
Отже, план перевезень не оптималний, і його можна поліпшити.
Удосконалення плану перевезень здійснюється наступним чином. У клітку, для якої не виконується умова (7.14), вписуємо поставку величиною Δ. Оскільки сума поставок по рядках і стовпцях повинна залишитися незмінною, то необхідно додати і відняти Δ з поставок в інших клітинах, обходячи їх у тій послідовності, при якій значення Δ компенсується відніманням і складанням зі значенням числа в клітці. Отримуємо замкнуту ламану лінію, яку прийнято називати циклом перерахунку.
При отриманні нового плану перевезень та визначенні величини поставок Δ необхідно користуватися таким правилом: починаючи з вільних кліток і рухаючись по циклу перерахунку, у вершинах циклу розставляємо почергово знаки + і -, потім переглядаємо поставки; записані в негативних вершинах, і вибираємо найменшу. Це число прибав-ляется до всіх поставок, записаним в позитивних вершинах, і вичитається з усіх поставок, записаних в негативних вершинах. Результати нового плану перевезень заносимо в табл. 7.8.
Таблиця 7.8 – Результати нового плану перевезень
Пункти відправлен-ня |
Допоміжні |
Пукти призначення і відстані |
Наявність вантажу |
|||
|
|
|
|
|||
|
4 |
2 |
3 |
3 |
||
|
0 |
4 4 |
8 |
3 |
3 12 |
100 |
|
1 |
3 |
3 10 |
4 |
4 18 |
80 |
|
3 |
7 |
5 |
6 8 |
6 |
240 |
Потребності |
|
160 |
90 |
120 |
50 |
420 |
Обчислення потенціалів табл. 7.8 проведено за умовою (11) для зайнятих клітин. Попередньо прийнято ![]() = 0.
= 0.
![]() +
+ ![]() = 3 при
= 3 при ![]() = 3,
= 3, ![]() = 0;
= 0;
![]() +
+ ![]() = 4 при
= 4 при ![]() = 3,
= 3, ![]() = 1;
= 1;
![]() +
+ ![]() = 5 при
= 5 при ![]() = 4,
= 4, ![]() = 1;
= 1;
![]() +
+ ![]() = 7 при
= 7 при ![]() = 4,
= 4, ![]() = 3;
= 3;
![]() +
+ ![]() = 6 при
= 6 при ![]() = 3,
= 3, ![]() = 3.
= 3.
Для всіх вільних клітин таблиці 7.8 умова ![]() +
+ ![]() ,
, ![]() -виконується, отже, отриманий оптимальний план перевезень. Значення цільових перевірок функцій для такого плану перевезень таке:
-виконується, отже, отриманий оптимальний план перевезень. Значення цільових перевірок функцій для такого плану перевезень таке:
W = 3-100 + 5-60 + 4-20 + 7-100 + 5-90 + 6-50 = 2130 (тис. км).
Примітка. Вище розглянуто варіант транспортної задачі в якій потреби у вантажах пунктів призначення дорівнюють запасу вантажу в пунктах відправлення;
![]() (7.29)
(7.29)
Модель такої транспортної задачі називається закритою. Якщо ж умова (7.15) виконується, то модель такої задачі називається відкритою.
У разі перевищення запасу над потребою, тобто, ![]() при вирішенні задачі вводиться фіктивний (п + 1)-й пункт призначення з потребністю
при вирішенні задачі вводиться фіктивний (п + 1)-й пункт призначення з потребністю ![]() і відповідну відстань (тариф), рівне нулю
і відповідну відстань (тариф), рівне нулю ![]() = 0, (i = 1, 2, .., m).
= 0, (i = 1, 2, .., m).
Аналогічно при ![]() , вводиться фіктивний (m + 1)-й пункт відправлення з запасом вантажу
, вводиться фіктивний (m + 1)-й пункт відправлення з запасом вантажу ![]() , і відстані (тарифи) покладаються рівними нулю:
, і відстані (тарифи) покладаються рівними нулю: ![]() = 0, (j = 1, 2, .., n). Цим завдання зводиться до звичайної (закритої) транспортній задачі.
= 0, (j = 1, 2, .., n). Цим завдання зводиться до звичайної (закритої) транспортній задачі.
7.7 Розробка раціональних маршрутів перевезень масових вантажів на підставі заявок клієнтів
Складання раціональних маршрутів перевезень масових вантажів має на меті досягнення максимального коефіцієнта використання пробігу автомобілів шляхом визначення порядку проходження автомобілів від місця розвантаження до місця навантаження з тією умовою, щоб загальний пробіг без вантажу був найменшим.
7.7.1 Постановка завдання
При вирішенні таких завдань відбираються ті заявки на перевезення вантажів, які збігаються за часом виконання перевезень і які можна здійснити одним і тим же рухомим складом.
Припустимо, що такі заявки відібрані, встановлені найкоротші відстані між усіма пунктами, обраний тип рухомого складу, визна-делено кількість поїздок з доставки вантажу від кожного постачальника відповідному споживачеві. Вихідні дані одного з варіантів подібного завдання представлені табл. 7.9, 7.10, де відповідно відображені добовий обсяг перевезень за заявками вантажовідправників і показники роботи автомобілів.
Таблиця 7.9 – Вихідні дані: кількість перевезеного вантажу кількість їздок
№ п/п |
Вантажовідправник |
Вантажоприймач |
Тип |
Кількість |
|||
т |
їздки |
||||||
1 |
Річковий порт |
|
Завод |
|
Пісок |
140 |
20 |
2 |
Річковий порт |
|
Завод ЗБК |
|
Щебень |
105 |
15 |
3 |
Котлован |
|
Будівництво 2 |
|
Грунт |
245 |
35 |
4 |
Пісщаний кар’єр |
|
Будівництво 1 |
|
Пісок |
336 |
48 |
Кожному відправникові присвоєно умовне позначення А, споживачу - Б з відповідними порядковими цифровими індексами. У таблиці 7.9 крім кількості перевезеного вантажу показано кількість їздок, яка визначена за показниками роботи обраного рухомого складу (табл. 7.10).
Таблица 7.10 – Показники роботи обраного рухомого складу
№ п/п |
Параметр |
Одиниця вимірювання |
Кількість |
1 |
Вантажопійомність МАЗ - 5551 |
т |
7,0 |
2 |
Середня технічна швидкість |
км/год |
22,0 |
3 |
Час в наряді |
год |
14,0 |
4 |
Норма часу на завантаження за їздку |
хв |
7,0 |
5 |
Норма часу на розвантаження за їздку |
хв |
6,0 |
6 |
Початок роботи пуктів розвантаження |
год |
7,0 |
Матриця відстаней між вантажними пункатми, відповідна схемі перевезень (рис. 7.6), представлена в табл. 7.11.
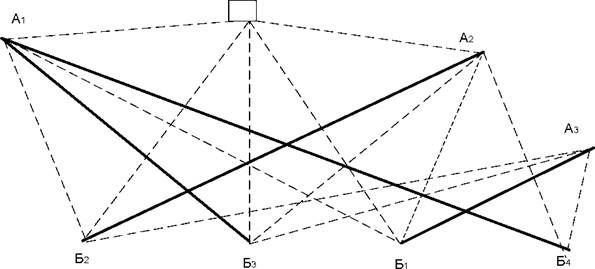
Рисунок 7.6 – Схема перевезень
Таблица 7.11 – Матриця відстаней між вантажними пункатми
Вантажні пункти |
|
|
|
АТП |
|
12 |
13 |
11 |
10 |
|
9 |
12 |
13 |
9 |
|
11 |
15 |
12 |
11 |
|
14 |
8 |
5 |
9 |
АТП |
6 |
4 |
7 |
0 |
7.7.2 Розробка раціональних маршрутів
На підставі заявок договірної клієнтури заповнюють розрахункову таблицю (наприклад методом північно-західного кута), в клітинах якої вказують кількість порожніх їздок з пунктів ![]() в пункти
в пункти ![]() і відстані між пунктами (останні проставляються у верхніх правих кутах відповідних клітин). Отримаємо початковий план холостих їздок. Перевіримо цей план на оптимальність, наприклад методом потенціалів, і доб'ємося такого розподілу порожніх їздок автомобілів, при яких їх пробіг без вантажу буде мінімальним.
і відстані між пунктами (останні проставляються у верхніх правих кутах відповідних клітин). Отримаємо початковий план холостих їздок. Перевіримо цей план на оптимальність, наприклад методом потенціалів, і доб'ємося такого розподілу порожніх їздок автомобілів, при яких їх пробіг без вантажу буде мінімальним.
Результати розрахунку оптимального розподілу їздок автомобілів без вантажу, забезпечують мінімальний порожній пробіг всіх автомо-білів, що беруть участь у планованих перевезеннях, наведено в табл. 7.12. У даній таблиці вказано, що з пункту ![]() в пункт А необхідно зробити 35 їздок без вантажу, з пункту
в пункт А необхідно зробити 35 їздок без вантажу, з пункту ![]() до пункту
до пункту ![]() – 20 їздок і т.д.
– 20 їздок і т.д.
Таблиця 7.12 – Результати розрахунку оптимального розподілу їздок
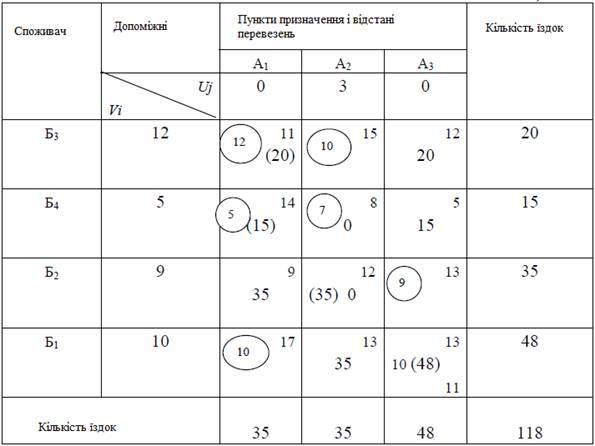
Після отримання оптимального плану розподілу порожніх їздок в цю ж таблицю вносимо план навантажених їздок (цифри в дужках).
У тих клітинах, де є дві цифри, призначаються митників маршрути, кількість їздок за якими одно найменшою цифрі. Так, в клітці А3 Б1 маємо маятниковий маршрут № 1: ![]()
![]()
![]()
![]() з 13 оборотами. Ця кількість їздок виключається з подальшого розгляду.
з 13 оборотами. Ця кількість їздок виключається з подальшого розгляду.
Коли всі митників маршрути знайдені, в матриці будуємо подружжя-рехугольние (шестикутні і т.д.) контури, всі вершини яких лежать в завантажених клітинах, причому вершини з навантаженого перевезення повинні чергуватися з вершинами порожніх їздок. У даному прикладі отримано два таких контуру, які показані пунктирними лініями. Кожен з них становить кільцевий маршрут.
Маршрут № 2:![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() - 20 оборотів;
- 20 оборотів;
Маршрут № 3:![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() - 15 оборотів.
- 15 оборотів.
Кількість оборотів на маршруті визначається найменшим числом у вершинах контуру. Обрана кількість їздок з клітин таблиці виключається. Рішення ведеться до повного виключення всієї кількості їздок з матриці.
Після призначення маршрутів необхідно вибрати початкові пункти навантаження на кільцевих маршрутах і визначити, яка кількість автомобілів слід направити на кожен маршрут, щоб забезпечити виконання плану перевезень.
Початковий пункт навантаження вибирається з умови мінімуму нульового пробігу ![]() . Для нашого прикладу мінімальний нульовий пробіг
. Для нашого прикладу мінімальний нульовий пробіг ![]() =
= ![]() +
+ ![]() = 4 + 10 = 14 км для початкового пункту навантаження А2. Схема кільцевого маршруту № 3 наведена на рис. 7.7.
= 4 + 10 = 14 км для початкового пункту навантаження А2. Схема кільцевого маршруту № 3 наведена на рис. 7.7.
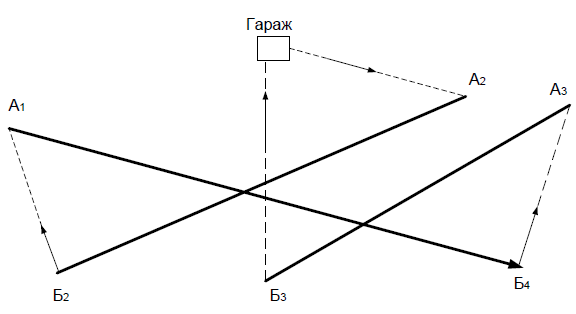
Рисунок 7.7 – Схема кільцевого маршруту №3
Перевезення за маршрутом можна починати з пункту ![]() або
або ![]() , тоді автомобіль буде повертатися в гараж з пункту
, тоді автомобіль буде повертатися в гараж з пункту ![]() або
або ![]() відповідно. Це доводиться часто робити з метою виключення одночасної подачі на один і той же пункт навантаження великої кількості автомобілів і створення черг, хоча при цьому нульові пробіги автомобілів можуть дещо збільшуватися.
відповідно. Це доводиться часто робити з метою виключення одночасної подачі на один і той же пункт навантаження великої кількості автомобілів і створення черг, хоча при цьому нульові пробіги автомобілів можуть дещо збільшуватися.
7.7.3 Розрахунок потрібного числа рухомого складу на маршруті
Розрахунок потрібного числа автомобілів на маршруті і коефіцієнта використання парку проводиться за нижче наведеними співвідношенням.
Число оборотів автомобілів по маршруту за час у наряді:
![]() (7.30)
(7.30)
де Т – час в наряді, год;
![]() – перший нульовий пробіг, км;
– перший нульовий пробіг, км;
![]() – другий нульовий пробіг, км;
– другий нульовий пробіг, км; ![]() - остання холоста їздка на маршруті, км;
- остання холоста їздка на маршруті, км;
![]() – середня технічна швидкість, км / год;
– середня технічна швидкість, км / год;
![]() – час обороту автомобіля на маршруті, ч.
– час обороту автомобіля на маршруті, ч.
![]() – маятниковий маршрут;
– маятниковий маршрут;
![]() – кільцевий маршрут,
– кільцевий маршрут,
де ![]() - відстань їздки з вантажем, км;
- відстань їздки з вантажем, км;
![]() - час вантажно-розвантажувальних робіт за їздку, год;
- час вантажно-розвантажувальних робіт за їздку, год;
![]() - довжина маршруту, км;
- довжина маршруту, км;
n - число їздок за оборот.
Потрібне число автомобілів на маршруті:
![]() , (7.31)
, (7.31)
де ![]() - плановий обсяг перевезень на маршруті за добу, т;
- плановий обсяг перевезень на маршруті за добу, т;
![]() - номінальна вантажопідйомність, т;
- номінальна вантажопідйомність, т;
![]() - коефіцієнт використання вантажопідйомність.
- коефіцієнт використання вантажопідйомність.
Коефіцієнт використання пробігу за день
![]() , (7.32)
, (7.32)
де ![]() - пробіг з вантажем автомобіля за день, км.
- пробіг з вантажем автомобіля за день, км.
![]() (7.33)
(7.33)
де ![]() - сумарний пробіг з вантажем за оборот автомобіля на маршруті;
- сумарний пробіг з вантажем за оборот автомобіля на маршруті;
![]() - cумарний нульовий пробіг, км;
- cумарний нульовий пробіг, км;
![]() - довжина маршруту.
- довжина маршруту.
Контрольні запитання
- Сформулюйте задачу лінійного програмування.
- Запишіть задачу лінійного програмування в матричної формі і у вигляді знаків підсумовування.
- Що таке область допустимих рішень, опорні точки і опорні рішення?
- Перерахуйте правила переходу від вихідної завдання лінійного програмування до двоїстої завданню.
- Послідовність виконання завдання лінійного програмування геометричним способом.
- Особливості вирішення завдань лінійного програмування сим-плекс-методом.
- Що таке канонічна форма запису задачі лінійного програмування?
- Послідовність виконання завдання лінійного програмування сим-плекс-методом.
- Сформулюйте «транспортну задачу».
- Послідовність рішення «транспортної задачі».
- Особливості запису і рішення відкритої «транспортної задачі».