---

---

8 МЕТОДИ ДИНАМІЧНОГО МОДЕЛЮВАННЯ

Динамічне програмування (dynamic programming) – особливий метод вирішення оптимізатора-заційну завдань. Особливістю даного методу є те, що для знаходження оптимального рішення завдання розбивається на етапи (кроки) і оптимальна рішення відшукується поступово крок за кроком.

Методом динамічного програмування вирішуються такі завдання автомобільного транспорту:

• завдання маршрутизації;
• завдання заміни обладнання та рухомого складу;
• оптимізація управління запчастинами;
• оптимізація розподілу ресурсів та ін

8.1 Постановка задачі

Нехай маємо деяку фізичну систему (автомобіль), яка з плином часу може міняти свій стан (процес старіння авто-мобіля тощо), тобто в системі відбувається якийсь процес. Поставимо за ¬ дачу керувати цим процесом.
Отже, система S (автомобіль) може з початкового стану перейти в кінцевий стан , але не просто, а під дією деякого управління U (рис. 8.1.)

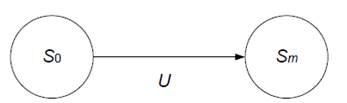
Рисунок 8.1 – Схема станів системи

Управління має бути таким, щоб воно дало деякий «виграш», який позначимо через W. Цей виграш залежить від управління, тобто:

W = f(U).                                                    (8.1)

Очевидно, що ми повинні знайти таке управління, при якому виграш буде максимальним, тобто:

,                                        (8.2)

де U – можливі управління;
u – оптимальне управління;
max – «максимум по u, тобто максимальне значення f(u) при всіх можливих управліннях U.
Отже, загальну задачу динамічного програмування можна сформульовані так: з безлічі можливих управлінь U треба знайти таке оптимальний управління U, яке переводить фізичну систему S з початкового стану  в кінцевий стан  так, щоб при цьому виграш W звертається в максимум.

8.2 Принципи оптимізації

Принципи оптимізації зводяться до наступного:
а) Процес переміщення системи зі стану  в стан  розбивається штучно або природно на кілька кроків (етапів) (рис. 8.2. та 8.3.).

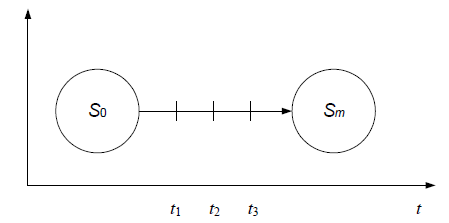
Рисунок 8.2 –Процес переміщення системи зі стану  в стан

У даному випадку маємо t кроків.
б) Виконується покрокова оптимізація (turn-based optimization), яка полягає в отриманні виграшу на кожному кроці.

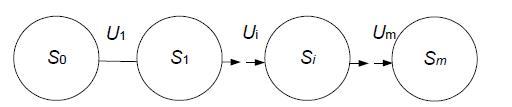
Рисунок 8.3 –Процес переміщення системи зі стану  в стан , розбитий на кілька кроків

Якщо виберемо на першому кроці управління , то виграш на цьому кроці від прийнятого управління складе:

.                                         (8.3)

Для i-го кроку з керуванням і  виграш складе:

 і т.д.                                   (8.4)
Тобто виграш на i-му кроці є функція стану і прийнятого управління.
Процедура побудови оптимального управління включає дві стадії: попередню (умовну); остаточну (безумовну).
Попередня (умовна) оптимізація (сonventional optimization) проводиться по кроках у зворотному порядку – від останнього кроку до першого. На попередній стадії визначається для кожного кроку умовне оптимальне управління і умовний оптимальний виграш.
Остаточна (безумовна) оптимізація проводиться також по кроках, але в природному порядку - від першого кроку до останнього.
На остаточній стадії визначається для кожного кроку остаточне (безумовне) оптимальне управління і безумовний оптимальний виграш.
В основі процедури оптимізації задач динамічного програмування лежить рівняння Беллмана, до розгляду якого і перейдемо.

8.3 Основне рівняння динамічного програмування

Нехай маємо задачу динамічного програмування, розглядаючу процес переходу системи S зі стану  у стан .
Для вирішення даної задачі процес переходу системи зі стану  в со-стояння  розбиваємо на m кроків. Отримуємо (рис. 8.4.).

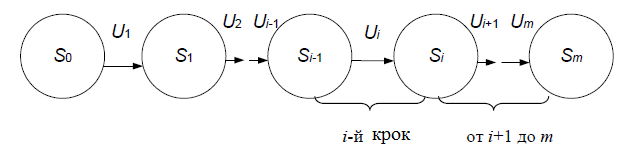Рисунок 8.4 – Процес переходу системи зі стану  в со-стояння  розбиваємо на m кроків

Будемо керувати цим процесом, тобто приймати управління  і т.д.
1. Виберемо на i-му кроці управління , яке дає на цьому кроці виграш ,

.                          (8.5)

Подібний виграш ми можемо мати на кожному кроці від 1 до m.
2. Позначимо оптимальний загальний виграш, одержуваний на всіх кроках наступних за i через

                                                 (8.6)

загальний виграш на кроках від (i+1), ... , до m, який вибирається оптимальним.
3. Таким чином, загальний виграш, який ми маємо на всіх кроках, починаючи з i- го, можемо представити формулою:

                       (8.7)

тобто загальний виграш дорівнює сумі виграшів:

• виграш на,i-му кроці -;
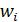• і оптимальний виграш на всіх наступних кроках, починаючи з,i + 1 до m - ()

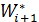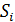4. Відповідно до принципу оптимізації, ми повинні вибирати на,-му кроці таке управління і, = і,, при якому виграш був би максимальним, тобто:

                     (8.8)

Вираз (8.1) характеризує умовний оптимальний виграш на всіх кроках з, i-го до m (до кінця) і називається рекурентним рівнянням Беллмана.
Обчислення складових виразу (8.1) починають з останнього т-го кроку.

8.3.1 Попередня (умовна) оптимізація

Використовуючи рівняння (8.1) визначимо умовний оптимальний виграш на останньому кроці m:

                         (8.9)

Зазначимо, що останній доданок у формулі (8.1) дорівнює 0, тому за  немає іншого стану.
Вираз (8.2) визначає умовний оптимальний виграш на останньому кроці, який досягається при управлінні:

.                                     (8.10)

Схематичні співвідношення (8.1) і (8.2) можемо проілюструвати рисунком 8.5.
Отже, знаючи виграш на т кроці, можемо знайти виграш на кроці m - 1 для чого використовуємо рекуррентную формулу (8.1), тобто використовуючи висловлювання (8.1), можемо побудувати весь ланцюжок умовних оптимальних управлінь і умовних оптимальних виграшів.
Дійсно, знаючи  можна по рекурентного рівняння Беллмана (7.1) знайти  і , а потім  і  і т. д. до останнього від кінця (першого) кроку.

 і                                       (8.11)

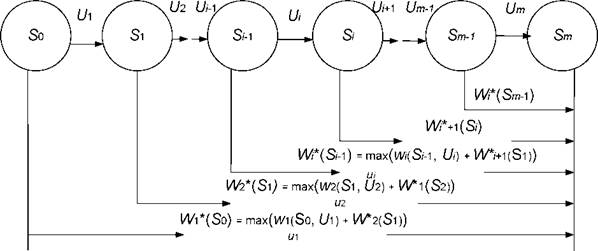
Рис. 8.5 – Ілюстрація співвідношення (7.1) і (7.2)

Функція  – є умовний оптимальний виграш за всю операцію, тобто на всіх кроках, починаючи з останнього, і до першого.
На цьому попередня оптимізація закінчується: знайдені умовно оптимальний виграш і умовні оптимальне керування для кожного кроку.

8.3.2 Остаточна (безумовна) оптимізація

Припустимо, що початковий стан  нам повністю відомо. Підставимо цей стан  у формулу для умовного оптимального виграшу ().
Отримаємо:
(),                                         (8.12)

а оптимальне управління на цьому кроці:

 ()                                           (8.13)

Далі, знаючи початковий стан  і керування , можемо знайти
стан  системи після першого кроку:

.                                    (8.14)

Знаючи стан , можна знайти оптимальне управління на другому
кроці
 ()                                          (8.15)
а потім
 ()                                     (8.16)
і т.д.
Таким чином, йдучи по ланцюгу (рис. 8.6.), Ми визначимо одним за одним всі кроки оптимального управління та оптимальне управління операцією в цілому
).                                    (8.17)

На цьому процес оптимізації закінчується.

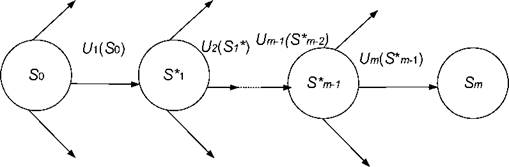
Рисунок 8.6 – Кроки оптимального управління

Принципи та методи динамічного програмування розглянемо на прикладі задачі вибору найкоротшого маршруту на транспортній мережі.

8.4. Задача про маршрутизації

8.4.1 Постановка завдання

Знайти найкоротший шлях з пункту А в пункт В на мережі, зображеної на рис. 8.7, де пункти позначені кружками, а що з'єднують їх шляхи відрізками (стрілками). Відстані  між пунктами проставлені над стрілками.
З точки зору інтересів оптимізації після кожного найближчого кроку (вибору найкоротшого відстані з точки -в точку ) То слід рухатися за маршрутом  -  -  -  - - В.

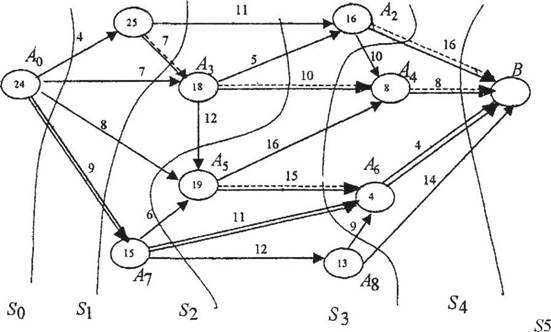
Рисунок 8.7 – Найкоротший шлях з пункту А в пункт В
Довжина цього маршруту (4 + 7 + 5 + 10 + 8) дорівнює 34.
Вирішивши цю задачу методом динамічного програмування ми переконаємося, що цей маршрут не є оптимальним.

8.4.2 Побудова математичної моделі

Нехай задана орієнтована мережа, що містить N точок (вузлів). Знайти найкоротший шлях з точки 1 в точку N (рис. 8.8), якщо задана матриця  відстаней з точки i, в точку j .

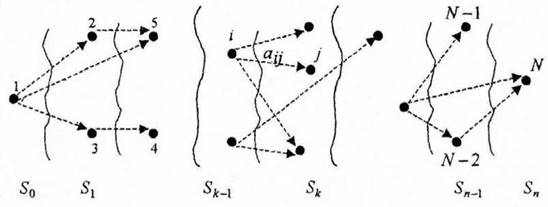
Рисунок 8.8 – Найкоротший шлях з точки 1 в точку N

Позначимо через   мінімальний шлях з точки i, в точку N. Оптимальний маршрут з будь-якої точки, повинен володіти тим властивістю, що яким би не був спосіб досягнення пункту i, подальше рішення повинне бути оптимальним для частини шляху, який починається в точці і (принцип оптимальності).
Нехай з точки i можемо перейти в току j, відстань між цими точками дорівнює . Точка j повинна вибратися таким чином, щоб шлях з j в N  був частиною оптимального з и в N. Позначимо мінімальний шлях із j
в N через . Тоді i вибирається з умови мінімізації суми:

                                             (8.18)

Таким чином отримуємо рівняння Беллмана.

                                          (8.19)

Для реалізації рівняння (7.3) розділимо умовно всі точки мережі на п множин за кількістю кроків 1, 2, ..., n (див. рис. 7.8.). До безлічі віднесем точки, з яких можна потрапити в N не більше ніж за n кроків, до  - точки з яких можна потрапити в N не більше ніж за n - 1 кроків і т.д.
Якщо i Є , то будемо вважати, що j Є . Тоді рівняння, (7.3) прийме вигляд
                          (8.20)

Оскільки точка N єдина і відноситься до безлічі , тоді

.                                         (8.21)

Безліч  складається з точок i, з яких можна потрапити в N не більше ніж за один крок, тому

,                        (8.22)

де  – умовні оптимальне управління (рішення) на n-му переході з точки i в N по найкоротшому шляху. Аналогічно для точок i Є :

,     (8.23)

і т.д. У підсумку умовної оптимізації отримаємо сукупність умовних оптимальних рішень , використовуючи які послідовно визначимо точки, відповідні оптимальним маршрутом.

8.4.3 Послідовність розв’язку задачі

Ррозв’язок. Віднесемо до безлічі S4 точки і , з яких можна по-пащу в точку B не більше ніж за один крок; до  - точки ,  і , з яких можна потрапити в точку В не більше ніж за два кроки; до  - точки
і , з яких можна потрапити в точку В не більше ніж за три кроки; до  - точку , (не більше ніж за чотири кроки до точки В), до  - точку .
Умовні оптимальні маршрути, що починаються в точці , і йдучі в точку , будемо зображати додаткової пунктирною стрілкою, а умовні мінімальні шляху від , до В записувати в гуртках точки . Спочатку знайдемо


Далі визначаємо

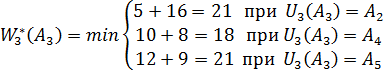
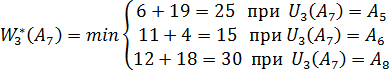
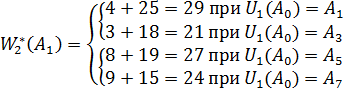
Отримуємо, що мінімальний шлях дорівнює  = 24. Відповідний маршрут проходить через точки , , , В. На рис. 8.7 він виділений подвійною лінією.

8.5 Задачі заміни обладнання

8.5.1 Постановка завдання

Однією з проблем, з якою доводиться стикатися при організації роботи автомобільного транспорту, є заміна старого обладнання (верстатів, агрегатів, машин) і автомобілів на нові.
Старе обладнання (автомобіль) має фізичний і моральний знос, в результаті чого зростають виробничі витрати з випуску продукції на старому обладнанні, збільшуються витрати на його ремонт та обслуговування, а разом з тим знижуються його продуктивність і ліквідна вартість.
Настає момент, коли старе обладнання (автомобіль) більш вигідно продати (замінити новим), ніж експлуатувати ціною великих витрат.
Оптимальна стратегія (optimal strategy) заміни обладнання полягає у визначенні оптимальних термінів заміни. Критеріями оптимальності при визначенні строків заміни можуть служити або прибуток від експлуатації, яку слід максимізувати, або сумарні витрати на експлуатацію протягом розглянутого проміжку часу, які підлягають мінімізації.
Домовимося вважати, що рішення про заміну обладнання приймається періодично на початку кожного проміжку (року), на який розбитий плановий період.
Основними функціональними характеристиками обладнання є при-ляють:
t - Вік обладнання (t = 0, 1, 2, 3, ..., n), де t = 0 - використання нового обладнання,
t = 1 - використання обладнання віку одного року і т.д.;
f(t) - вартість продукції (для автомобіля - виручка за транспортні послуги), виробленої за рік на обладнанні віку t;
r(t) - експлуатаційні витрати за рік на обладнання віку t;
φ(t) - залишкова вартість обладнання віку t;
Р - ціна нового обладнання;
 - початковий вік обладнання;
n - тривалість планового періоду (кількість років у плановому періоді).
Схема можливих станів обладнання може виглядати так (рис. 8.9).

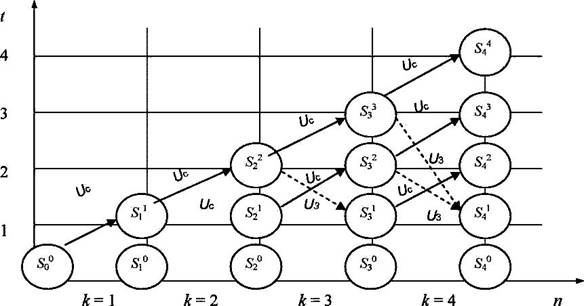
- збереження і тривалість використання обладнання;  - заменяемость обладнання новим; - cтан обладнання, відповідне віку t

Рисунок 8.9 –Схема можливих станів обладнання

8.5.2 Побудова математичної моделі

Поставлену задачу можна розглядати як завдання динамічно го програмування, в якій в якості системи S виступає устаткування. Стану цієї системи визначається фактичним часом користування обладнання (його віку) t, тобто описується єдиним параметром t.
Алгоритм рішення задачі методом ДП реалізується у два етапи.
Перший етап. При русі від початку n-го року до початку 1-го року для кожного допустимого стану обладнання знаходиться умовне оптимальних управління (рішення) – u(t).
Другий етап. При русі від початку 1-го року до початку n-го року з ус-умовних оптимальних рішень складається оптимальний план заміни
обладнання – (t).
Розглянемо n-кроковий процес (див. рис. 8.9), вважаючи k-м кроком номер k-го року від початку експлуатації (k = 1, 2, 3, ..., n). Рівняння на k-му кроці вибирається з двох можливих рішень:  - зберегти і продожити використання старого обладнання або  - замінити обладнання новим.
Стан  системи на початку k-го кроку характеризується параметром t - вік обладнання, який може приймати значення 0, 1, 2, ... , k - 1, тобто . Якщо до початку k-го кроку система перебуває в стані  і вік її дорівнює t рокам (  = t), то під впливом рівняння  врешті k-го кроку вона перейде в стан  з віком обладнання t + 1 ( = t + 1) (рис. 8.9), тобто вік обладнання збільшиться на один рік. Під впливом рівняння , прийнятого на k-му кроці, система перейде в стан з віком обладнання, рівним одному року. Заміну справили на початку k-го кроку ( = 1).
Визначимо прибуток на k-му кроці (показник ефективності k-го кроку) відповідну кожному з альтернативних управлінь  і .
Вибираючи на k-му кроці управління і, ми зможемо виробити продукцію вартістю f(t) на старому обладнанні, що зажадає витрат r(t), тому прибуток дорівнює f(t)-r(t). Позначимо її через:

.                                 (8.24)

При управлінні  отримаємо дохід f(t) від продажу старого обладнання (ліквідну вартість) та f(0) від виробленої на новому обладнанні продукції, витративши Р гривень на придбання нового обладнання, і r(0) - на утримання нового обладнання. У цьому випадку прибуток складе:

.                         (8.25)

Так як на останньому етапі процесу планування ми можемо діяти без врахування попередніх етапів і вважати, що оптимальне управління на останньому етапі має забезпечити максимальний дохід за останній рік, то функціональне рівняння, що відбиває можливі рішення, буде наступним:

              (8.26)

Порівнявши ці дві величини для всіх можливих i <n отримаємо значення  і відповідне значення оптимального управління .
Припустимо, що для всіх значень t - про стан системи максимальний прибуток, отримана за п - k кроків з k + 1-го по n-й включно. Тому основні рекурентні співвідношення можна за-писати у вигляді:

 (8.27)
У рівнянні (7.5) величина  - умовна максимальна прибуток, отримана за n - до кроків, якщо до початку (k + 1)-го кроку системи знаходились в змозі  і t = 1 (вік обладнання становив 1 року).

8.5.3 Послідовність розв’язку задачі

Рішення завдання заміни обладнання методом динамічного програмування розглянемо на конкретному прикладі.
Приклад. Скласти план заміни обладнання протягом п'яти років, при якому загальний прибуток за даний період часу максимальна, якщо витрати, пов'язані з придбанням і установкою нового обладнання складають
40 тис. грн. Залежність продуктивності обладнання від часу його використання, а також залежність витрат на утримання та ремонт обладнання при різному часі його використання приведені в табл. 8.1.
        
Таблиця 8.1 – Залежність продуктивності обладнання від часу його використання, витрат на утримання та ремонт обладнання при різному часі його використання

1. Знаходження рішеня вихідної задачі починаємо з визначення умовного оптимального управління(рішення) для останнього 5-го року і знаходим множину допустимих станів обладнання до початку данного року. Так як в початковий момент є нове обладнання ( = 0), то вік обладнання до початку 5-го року може складати 1,2,3,4 роки. Тому допустимі стина системи на даний період часу такі:  =1;  = 2,  = 3,  = 4. Для кожного з цих станів знайдемо умовне оптимальне рішення і відповідне значення функції .
Використовуючи рівняння (8.4) і співвідношення  = 0 (так як розглядуваний останній рік розрахункового періоду), отримаєм:

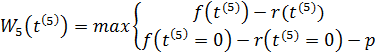                 (8.28)

Підставляючи тепер в формулу (8.6) замість  його значення, яке рівне 1; і приймаючи до уваги данні таблиці 8.1, знаходим:

.
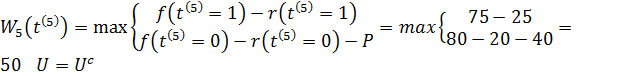Значить, умовне оптимальне рішення в даному випадку – зберегти обладнання. Проведемо аналогічні розрахунки для інших допустимих станів обладнання до початку 5-го року. Результати зводимо в табл. 8.2.

;
;
.

  Таблица 8.2 – Результати розрахунків

2. Розглянемо тепер можливі стану обладнання до початку 4-го року. Очевидно, що допустимими станами = 1, = 2, = 3. Для кожного з них визначається умовне оптимальне рішення і відповідне значення функції  Для цього використовуємо рівняння (8.5) і дані табл. 8.1, 8.2. Так, зокрема, для  маємо:

.

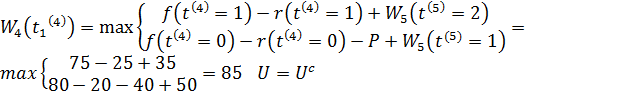Значить, умовне оптимальне рішення в даному випадку зберегти обладнання. Проведемо аналогічні обчислення для інших допустимих станів обладнання до початку 4-го року.

;

.

Отримані результати розрахунків занесемо в табл. 8.3.
3. Визначаємо тепер умовне оптимальне рішення для кожного із допустимих станів обладнання до початку 3-го року. Очевидно, що такими станами являються , . У відповідності з рівнянням (8.5) і табл. 8.1, 8.3 маємо:
Таблица 8.3 – Результати розрахунків

;
.

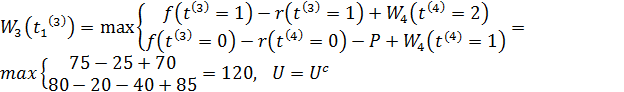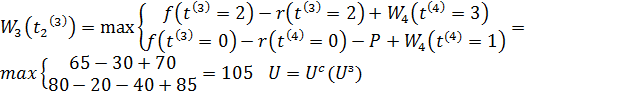З останнього виразу видно, що якщо до початку 3-го року вік обладнання становить 2 роки, то незалежно від того, чи буде прийнято рішення  чи . величина прибутку виявиться однією і тією ж. Це означає, що в якості умовного оптимального рішення можна взяти будь-яке, наприклад . Отримані значення для  і відповідні умовні оптимальні рішення записуємо в табл. 8.4.

Таблиця 8.4 – Отримані значення для  і відповідні рішення

4. Нарешті, розглянемо допустимі стану обладнання до початку 2-го року. Очевидно, що на даний момент часу вік обладнання може бути рівний тільки одному року. У відповідності з рівнянням (8.5) маємо (табл. 8.5):

.

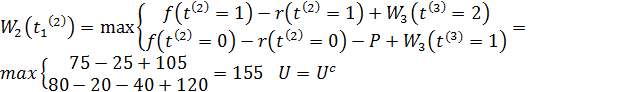Таблиця 8.5 – Результати розрахунків

5. В початковий момент встановлено нове обладнання ( = 0). Проблеми вибору між збереженням і заміною обладнання не існує обладнання слід зберегти. Умовним оптимальним рішенням є , і значення функції:

= 80 - 20 + 155 = 215

6. В результаті реалізації другого етапу обчислювального процесу. складається в проходженні всіх розглянутих кроків з початку першого до початку п'ятого року, максимальна прибуток підприємства може дорівнювати 215 тис. грн., що відповідає оптимальному плану заміни устаткування.
7. Для 1-го року рішення єдине - треба зберегти устаткування. Значить, вік обладнання до початку 2-го року дорівнює одному року, та обладнання (згідно табл. 8.5) треба зберегти. Реалізація такого рішення призводить до того, що вік обладнання до початку 3-го року стає рівним двом рокам, та обладнання (згідно табл. 8.4) треба зберігати, тобто його вік до початку
4-го року стає рівним трьом рокам, та обладнання (згідно табл. 8.3) треба замінювати. Після заміни обладнання його вік до початку 5-го року складе один рік. Як видно з табл. 8.2, при такому віці устаткування його міняти не слід. Отже, виходить оптимальний план заміни обладнання (рис. 8.10).

Рисунок 8.10 – Оптимальний план заміни обладнання

Контрольні запитання

1. Які завдання автомобільного транспорту вирішуються методами ді-наміческіх програмування.
2. Сформулюйте загальну задачу динамічного програмування.
3. Перерахуйте принципи оптимізації завдань динамічного про-граммирования. Запишіть основні рівняння динамічного програмування (рівняння Беллмана) і перепишіть його складові.
4. Особливості попередньої (умовної) оптимізації.
5. Особливості остаточної (безумовної) оптимізації.
6. Сформулюйте задачу про маршрутизації.
7. Запишіть математичну модель вирішення задачі про маршрутіза ¬ ції методом динамічного програмування.
8. Послідовність рішення задачі про маршрутизації методом динамічного програмування. Сформулюйте завдання про заміну обладнання.
9. Запишіть математичну модель вирішення задачі заміни обо ¬ ладнання методом динамічного програмування.
10. Послідовність рішення задачі заміни обладнання методом динамічного програмування.

 

---