Практичне заняття № 2
Проектування робочого процесу технологічного комплексу
Функціональні зв’язки складових систем І та ІІ вібропресового обладнання в аналітичній формі, розглянуті, головним чином, на рівні внутрішніх системних зв’язків між параметрами заготовки та ІВПМ. Сукупність міжсистемних функціональних зв’язків досліджуваного обладнання в аналітичній формі з врахуванням параметрів всіх складових систем являє собою математичну модель робочого процесу ВУП, на основі якої можливий розв’язок задач його оптимізації.
Згідно з установленими для ІВПМ зв’язками (рис. 2.1) параметри р2, що характеризують робочий процес (система ІІ) визначаються параметрами р1 та р3, які пов’язані відповідно з об’єктом обробки (система І) і машиною (система ІІІ). Реалізація заданих параметрів р3 відбувається в результаті взаємодії підсистем ІІІ.1...ІІІ.4. Величина р3 залежить від значень параметрів р1. Дослідження функціонального міжсистемного зв’язку виду Ф1 (р1, р3), проведене шляхом фіксації кінцевих значень параметрів р1 для визначених значень р3, виявилось достатньо складним та трудомістким, а для деяких випадків і недостатньо коректним, оскільки враховувалися не всі фактори (параметри), що впливають, в тому числі р2.
Тому при вивченні можливості виявлення функціонального зв’язку між параметрами систем І, ІІ, ІІІ вібропресового обладнання в аналітичній формі необхідно провести попередній детальний аналіз даних параметрів з метою виділення серед них основних, визначення яких, виходячи із сукупності решти параметрів систем, неможливо.
Ф (р1, р2, р3) (2.1)
Стан системи І ІВПМ можна охарактеризувати поточними значеннями фізико-механічних та геометричних параметрів заготовки: середньою щільністю (rзі, кг/м3); масою навішування (mзаг, кг); динамічним модулем умовної пружності (Kзі, МПа); площею відкритої поверхні з боку пуансона (Sзаг, м2); висотою (hзі, м). Для заготовок складної конфігурації крім вказаних параметрів необхідно врахувати площу перерізу по лінії дії навантаження (Sоі, м2), периметр даного перерізу (Пі, м) і лінійний середньостатистичний розмір частинки матеріалу (а, м).
Аналіз сукупності перерахованих параметрів р1 заготовки показує, що ряд з них (з індексом “і”) в процесі ВУП змінюється від значень, що характеризують початковий стан заготовки (і=0) в підсистемі І.1, до значень, що характеризують її кінцевий стан (і=k) в підсистемі І.2.
З метою скорочення загального числа параметрів р1 за умови збереження потрібної інформації про стан заготовки (система І), а також виключення другорядних параметрів виконаємо такі додаткові заходи:
- введемо параметр 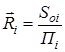 , що характеризує геометричну форму заготовки за аналогією з параметром „гідравлічний радіус” [57] і визначимо його як „геометричний фактор” (Ri, м) для заготовок простої конфігурації
, що характеризує геометричну форму заготовки за аналогією з параметром „гідравлічний радіус” [57] і визначимо його як „геометричний фактор” (Ri, м) для заготовок простої конфігурації ![]() ;
;
- введемо поняття відносної щільності 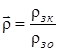 , що дозволяє охарактеризувати кінцевий стан заготовки у порівнянні із початковим і розглядати „геометричний фактор” R0 тільки для початкового стану;
, що дозволяє охарактеризувати кінцевий стан заготовки у порівнянні із початковим і розглядати „геометричний фактор” R0 тільки для початкового стану;
- виключимо із сукупності параметрів р1 параметр Kзі, який разом із параметрами ![]() (або hзі) та rзі визначає фактор часу (t0, с) – тривалість зовнішнього імпульсного силового впливу на заготовку, що є основним параметром робочого процесу (система ІІ), оскільки при об’єднанні параметрів систем ІВПМ один з них буде другорядним.
(або hзі) та rзі визначає фактор часу (t0, с) – тривалість зовнішнього імпульсного силового впливу на заготовку, що є основним параметром робочого процесу (система ІІ), оскільки при об’єднанні параметрів систем ІВПМ один з них буде другорядним.
В результаті реалізацій наведених вище заходів число основних параметрів системи І скорочується до ряду: ![]() . Однак для проведення досліджень багатофакторних систем загальне число параметрів доцільно зменшити і розглядати комплексно [78]. Для виділених основних параметрів системи І таким комплексним параметром може бути добуток R0·Sзаг (або hз0·Sзаг), що характеризує початковий об’єм заготовки. З врахуванням параметра R0·Sзаг для заданої величини rз0 не важко визначити mзаг.
. Однак для проведення досліджень багатофакторних систем загальне число параметрів доцільно зменшити і розглядати комплексно [78]. Для виділених основних параметрів системи І таким комплексним параметром може бути добуток R0·Sзаг (або hз0·Sзаг), що характеризує початковий об’єм заготовки. З врахуванням параметра R0·Sзаг для заданої величини rз0 не важко визначити mзаг.
У зв’язку з вищевикладеним, скорочену сукупність параметрів системи І можна записати у вигляді
р1 ![]() .
(2.2)
.
(2.2)
Основні параметри системи ІІ характеризують спосіб і режим силового впливу системи ІІІ на систему І. До даних параметрів р2, крім виділеного раніше t0, відносяться: зусилля додаткового статичного навантаження заготовки (Рст, Н), максимальне зусилля навантаження заготовки (Fз.max, Н) в процесі ВУП заготовки, загальне число ходів робочого столу ІВПМ (n) і частоту (fр, Гц) їх здійснення. Причому параметри n та fр можна об’єднати і описати одним параметром, що характеризує повний час робочого процесу (tвуп = n·fр-1, с).
Сукупність основних параметрів системи ІІ подамо у вигляді
р2 ![]() .
(2.3)
.
(2.3)
На основі параметрів (2.3) обираються параметри р3 системи ІІІ. У випадку, що нами розглядається (див. рис. 1.1) системою ІІІ є ІВПМ, що характеризується параметрами ГІП Eа, Wа, Kпр, Qн1, віброзбуджувача р1 та системи рухомих ланок m1, m2, m3, су, св. Параметри прес-форми аналогічні геометричним параметрам заготовки і враховуються в системі І.
Відомі аналітичні залежності, що установлюють зв’язок між вказаними параметрами р3 дозволяють однозначно обрати серед них основні. Використовуючи даний підхід, розглянемо комплекс параметрів {Ea, Wa, p1, Kпр}, об’єднаних відомою залежністю. В даному комплексі будь-які три параметри однозначно визначають четвертий, який можна виділити в число основних параметрів системи ІІІ. З врахуванням експериментальних даних основним параметром слід вважати енергію Еа.
До основних параметрів системи ІІІ необхідно віднести маси m1, m2 та жорсткість пружин повернення су. При цьому вважаємо, що маса станини m3 та жорсткість віброізоляторів св достатньо великі і не впливають на хід робочого процесу.
Використовуючи відношення m2/m1=a (m2=am1), параметри конструкції ІВПМ при незмінній масі робочого столу доцільно записати як m1, a·m1, су.
Для системи ІІІ скорочена сукупність основних параметрів записується таким чином
р3 {Ea, m1, a, m1, су} . (2.4)
В результаті об’єднання основних параметрів систем (2.2) – (2.4) знаходимо сукупність параметрів технологічного комплексу
р1р2р3![]() . (2.5)
. (2.5)
При визначенні параметрів сукупності (2.5) можна виключити постійні за величиною конструктивні параметри ІВПМ m1 та су, замість зусилля Fз.max розглянути зовнішнє примусове зусилля, яке однозначно визначається за допомогою незалежних параметрів Ea, m1, t0, су, а зусилля статичного навантаження Рст з врахуванням параметра Sзаг замінити питомим статичним зусиллям Руд = Рст/ Sзаг. У зв’язку з вищевикладеним, загальне число параметрів порівняно із (2.5) скорочується до восьми, за допомогою яких функціональний зв’язок (2.1) може бути описане залежністю
![]() (2.6)
(2.6)
Вивчення можливості подання функціональної залежності (2.6) у вигляді аналітичного виразу, що зв’язує основні параметри комплексу, показало, що розв’язання даної задачі теоретичним шляхом утруднено. Основною причиною цього, на наш погляд, є зміна з ущільненням неоднорідного середовища порошкового матеріалу заготовки функції його стану. У зв’язку з цим, теоретичний розв’язок може бути знайденим тільки для деяких станів заготовки, при цьому ряд параметрів комплексу залишаються не врахованими.
Для отримання залежності (2.6) в аналітичній формі можна використати наближені методи [2], основані на обробці результатів повного факторного експерименту (ПФЕ). Залежність, отримана таким чином, має окремий характер і може бути використана для розв’язання задач оптимізації параметрів робочого процесу ВУП в обмеженому діапазоні їх зміни.
В даному випадку, на нашу думку, перспективними є методи подібності та моделювання [78], які дозволяють розглядати робочий процес як клас подібних явищ, а “еталонні” зразки – як моделі об’єктів обробки (заготовок).
З цією метою основні параметри технологічного комплексу на основі p-теореми [113] перетворюються у загальні змінні (критерії подібності), а аналітична залежність між ними записується у вигляді критеріального рівняння подібності в степеневій формі. Охоплюваний даним рівнянням клас подібних явищ визначається на основі зворотної теореми подібності [113]: робочі процеси ВУП можна вважати подібними, якщо вони мають однакові визначальні критерії і подібні умови однозначності.
Умови однозначності або граничні крайові умови ВУП в загальному випадку визначаються такими основними параметрами технологічного комплексу:
- геометричними, що характеризують форму і розміри об’єкта обробки – ![]() ;
;
- фізичними, що характеризують фізичні властивості об’єкта обробки – ![]() ;
;
- початкового стану системи – ![]() ;
;
- взаємодії об’єкта обробки та зовнішнього середовища (прес-форми) – ![]() ;
;
- граничними, що характеризують протікання процесу в граничних точках об’єкта обробки та зовнішнього середовища – ![]() ;
;
- часу, що характеризує особливості протікання процесу в часі – ![]() .
.
Характерною особливістю даних параметрів є їх одночасна приналежність до різних умов однозначності.
В укладанні критеріального рівняння використовуємо результати аналізу формул розмірностей (табл. 2.1) основних параметрів, виділених в (7.6).
Для трьох незалежних (k=3) одиниць розмірності MLT, достатніх для опису механічних систем даного типу, критеріальне рівняння подібності містить m–k=5критеріїв подібності, причому будь-який з них є функцією інших m–k–1=4 критеріїв.
У випадку, що розглядається, критеріальне рівняння подібності має вигляд
π=f (π1, π2, π3, π4) (2.7)
і містить тільки чотири змінні – визначальні критерії подібності, для яких слід планувати ПФЕ.
Таблиця 2.1 – Формули розмірностей основних параметрів технологічного комплексу
| Параметр комплексу | Розмірність | Параметр комплексу | Розмірність | ||||
| М, кг | L, м | Т, с | М, кг | L, м | Т, с | ||
|
|
0 | 0 | 0 | Еа, Дж | 1 | 2 | -2 |
| Руд, Па | 1 | -1 | -2 | а, м | 0 | 1 | 0 |
|
|
0 | 0 | 1 | tвуп, с | 0 | 0 | 1 |
| R0·Sзаг, м3 | 0 | 3 | 0 |
|
1 | 0 | 0 |
Визначальними критеріями подібності в рівнянні (2.7) для основних незалежних параметрів технологічного комплексу Руд, R0 · Sзаг, ![]() можуть служити узагальнені змінні
можуть служити узагальнені змінні
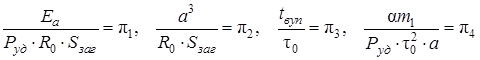 , (2.8)
, (2.8)
а функцією відгуку або не визначальним критерієм подібності – основний параметр ![]() .
.
З врахуванням (2.8) критеріальне рівняння набуває (2.7) приймає вигляду
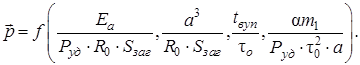 (2.9)
(2.9)
Критерії подібності або узагальнені змінні, що містяться в рівнянні (2.9), мають визначене фізичне значення. Для досліджуваного процесу їх можна охарактеризувати таким чином:
p1 – відношення щільності заготовки, досягнутої після завершення процесу формоутворення, до щільності заготовки у вихідному стані;
p2 – відношення енергії, що витрачається на здійснення одного робочого ходу ІВПМ, до енергії напруженого стану заготовки під дією статичного навантаження у вихідному стані;
p3 – відношення умовних об’ємів частинки порошкового матеріалу і заготовки у вихідному стані;
p4 – відношення повного часу процесу ВУП до часу дії зовнішньої примусової сили (є по суті стандартним критерієм подоби) Струхана [78] або критерію гомохронності;
p5 – відношення динамічного зусилля навантаження заготовки до його статичної складової (є по суті стандартним критерієм подібності Ньютона [78]).
Аналітичний зв’язок між критеріями подібності або узагальненими перемінними, що входять до рівняння (2.7) з врахуванням відомих рекомендацій [2, 78] можна подати у вигляді степеневої залежності
![]() (2.10)
(2.10)
де А – постійна, що відображує вплив на процес неврахованих факторів, наприклад, вмісту наповнювача, відносну нерівнощільність і т.п.; a, b, g, d – показники степеню, що визначаються експериментально.
Значення постійної А і показників степеню a, b, g, d у критеріальному рівнянні (2.10) знаходяться за відомою [78] методикою за допомогою матриць планування ПФЕ типу 24, розроблюваних для процесів ВУП „еталонних” зразків із визначених порошкових матеріалів.
Критеріальні рівняння подібності, отримані у вигляді (2.10), можуть бути використані при проектуванні процесів ВУП заготовок в реальних технологічних комплексах, наприклад, для розрахунку масштабних коефіцієнтів переходу [78].
В якості незалежних базисних параметрів при плануванні ПФЕ можна взяти ![]() для яких базисний визначник D≠0 [78]. Для прийнятих незалежних параметрів
для яких базисний визначник D≠0 [78]. Для прийнятих незалежних параметрів
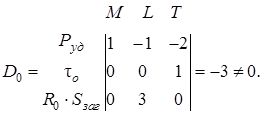 (2.11)
(2.11)
В цьому випадку визначальні критерії подібності або узагальнені змінні знаходяться у вигляді
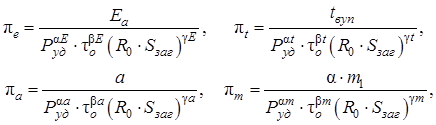 (2.12)
(2.12)
а невизначальний критерій відповідає відносній густині
![]()
Для знаходження показників степенів для незалежних параметрів використовувалась відома [78] методика, згідно із якою, наприклад,
![]() (2.13)
(2.13)
де ![]() ,
, ![]() ,
, ![]() – визначники, одержані шляхом підстановки у відповідні горизонтальні рядки базисного визначника D0 формули розмірності параметра
– визначники, одержані шляхом підстановки у відповідні горизонтальні рядки базисного визначника D0 формули розмірності параметра ![]() :
:
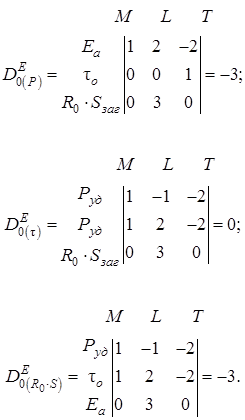 (2.14)
(2.14)
Шляхом підстановки в (2.12) значень виразів (2.13), одержаних з врахуванням (2.11) та (2.14), знаходяться показники αЕ = 1, βЕ = 0, γЕ = 1.
Аналогічно, підстановкою у D0 формули розмірностей [α], [tвуп] та [α·m1] знаходяться інші показники степенів у виразах (2.12):
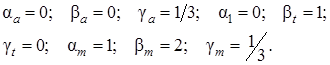 (2.15)
(2.15)
Після підстановки (2.15) в (2.12) визначальні критерії можуть бути записані такими виразами:
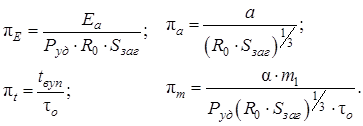 (2.16)
(2.16)
Після еквівалентних перетворень [78], припускаючи ![]() визначальні критерії, або узагальнені змінні можна подати у вигляді:
визначальні критерії, або узагальнені змінні можна подати у вигляді:
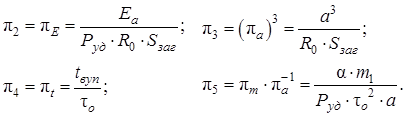 (2.17)
(2.17)
Отримані критерії (2.17), наприклад, π4 можна розглядати як стандартний критерій подібності [2, 78] Струхана (πSh) або критерій гомохронності (πSh), якщо вважати
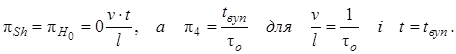
Критерій π5 можна розглядати як стандартний критерій Ньютона πNe:
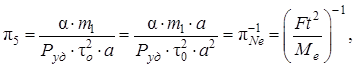
де руд·а2 ≡ F, τ02 ≡ t2, α·m1 ≡ M та a ≡ l.
В даній монографії визначальні критерії (2.17) використані для запису критеріального рівняння подібності (2.9). Така форма запису, отримана з врахуванням результату попередніх експериментів має найбільшу простоту та гнучкість.
Показники степенів критеріального рівняння та постійна, що відображують вплив на процес неврахованих факторів, визначались на основі багатофакторного експерименту.
Оскільки в експерименті беруть участь чотири фактори (π2, π3, π4, π5), можна проводити ПФЕ 24 або ДФЕ 24-1 [78]. На нашу думку, перевагу має ПФЕ 24, при постановці якого не має необхідності виявляти статично несуттєву взаємодію різних факторів, що пов¢язано зі значними витратами часу.
Основні рівні факторів πі0 встановлювались сукупністю найраціональніших параметрів процесу ВУП для досліджуваних порошкових матеріалів М1, М2, М3, М4, а інтервали зміни πін–πів визначались виходячи з умов роботи ІВПМ-5Л та вимог технологічного процесу.
Вказані фактори зручно представити у вигляді нових змінних:
![]() (2.18)
(2.18)
В цьому випадку умови ПФЕ декілька змінюються, оскільки необхідне корегування, наприклад, нижнього рівня інтервалу варіювання фактора πін, вважаючи, що основний і верхній рівні факторів в обох системах є незмінними:
![]() (2.19)
(2.19)
В нових змінних
![]() (2.20)
(2.20)
Тоді нижній рівень фактора після корегування визначається за допомогою виразу
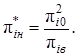 (2.21)
(2.21)
Після постановки ПФЕ 24 в нових змінних аналітичний зв¢язок між ними на першому етапі досліджень можна подати поліномом першого степеня [2] у вигляді
![]() , (2.22)
, (2.22)
коефіцієнти якого а0, а1, а2, а3, а4 знаходяться за відомим алгоритмом [78].
В таблиці 2.2 наведені умови, а в таблиці 2.4 план та результати ПФЕ 24 досліджень процесу ВУП “еталонних” зразків з порошкового матеріалу М2.
Розрахунок коефіцієнтів полінома (2.22) здійснений за відомою формулою [78]
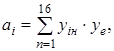 (2.23)
(2.23)
де уе – середній відгук по трьох точках; уin – значення уі в n-oму досліді.
Достовірність одержаної залежності (2.23) перевірена методом статистичного аналізу.
Для характеристики помилок встановлені дисперсії коефіцієнтів полінома (7.22) за відомою формулою [78]
![]() (2.24)
(2.24)
де ![]() – дисперсія дослідів; N – кількість серій дослідів (N=16); m – кількість дослідів в серії (m=3).
– дисперсія дослідів; N – кількість серій дослідів (N=16); m – кількість дослідів в серії (m=3).
Дисперсія дослідів (з врахуванням даних табл. 2.3)
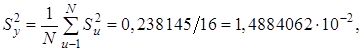 (2.25)
(2.25)
де 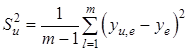 – оцінка дисперсії в точках досліду (див. графу 10 табл. 2.4); l - номер досліду в серії (l =1, 2, 3); yе – середній відгук по трьох точках (див. графу 9 табл. 2.3).
– оцінка дисперсії в точках досліду (див. графу 10 табл. 2.4); l - номер досліду в серії (l =1, 2, 3); yе – середній відгук по трьох точках (див. графу 9 табл. 2.3).
Підстановка результату (2.25) в (2.24) дає
![]() 1,4884062·10-2/16·3 = 3,1008462·10-4.
1,4884062·10-2/16·3 = 3,1008462·10-4.
Звідки
![]() 1,7609219·10-2.
1,7609219·10-2.
Статистична значущість коефіцієнтів аі перевірялась за робочим критерієм Ст’юдента [78], знайденим з виразу
![]() (2.26)
(2.26)
і зіставленим з табличним значенням [177] критерію tSt=2,04, що обчислювався для рівня значущості 0,05 і степеня вільності ft=N(m-1)=32.
В розглянутому випадку умовa tSpi > tSt не виконується тільки для коефіцієнта а2 (tSp2=0,0217/1,7609219·10-2=1,232 < tSt), що свідчить про його статистичну незначущість і дозволяє взяти а2=0.
Неадекватність емпіричної моделі для кількості дослідів в серії m>1 і кількості коефіцієнтів в поліномі (2.22) меншим N=16 перевірена за критерієм Фішера [2]:
![]() (2.27)
(2.27)
де ![]() – оцінка дисперсії адекватності.
– оцінка дисперсії адекватності.
За відомою формулою [78]
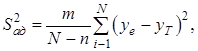 (2.28)
(2.28)
де n – число статистично значимих коефіцієнтів апроксимуючого полінома (n=4); ![]() – відгук, розрахований за виразом (2.22) і наведений в табл. 7.3 (графа 11).
– відгук, розрахований за виразом (2.22) і наведений в табл. 7.3 (графа 11).
З врахуванням даних табл. 2.3 для n=4
![]() 3·0,113247/(16-4) = 2,831175·10-2,
3·0,113247/(16-4) = 2,831175·10-2,
Тоді розрахунковий критерій Фішера за виразом (2.27)
![]() 2,831175·10-2/1,488062·10-2 ≈1,902.
2,831175·10-2/1,488062·10-2 ≈1,902.
Табличне значення критерію Фішера ![]() 2,07 [177] для рівня значущості 0,05 для степеней вільності дисперсії адекватності
2,07 [177] для рівня значущості 0,05 для степеней вільності дисперсії адекватності ![]() = 12 і дисперсії відновлюваності
= 12 і дисперсії відновлюваності ![]() =32.
=32.
Оскільки ![]() , то рівняння є адекватним з надійністю виведення 0,95
, то рівняння є адекватним з надійністю виведення 0,95
При перевірці нуль-гіпотези [2] встановлено, що полінома першого степеню достатньо для описання шуканої залежності. Так середнє значення дослідів в центральній точці ![]() = 0,46536319≈0,4654, а похибка експерименту Sy = 0,122 (див. вираз (2.25)).
= 0,46536319≈0,4654, а похибка експерименту Sy = 0,122 (див. вираз (2.25)).
Отже, ![]() = |0,4545 – 0,4654| = 0,0109 < Sy, що свідчить про відсутність квадратичних ефектів і адекватності лінійної моделі.
= |0,4545 – 0,4654| = 0,0109 < Sy, що свідчить про відсутність квадратичних ефектів і адекватності лінійної моделі.
Після потенціювання рівняння (2.22) та підстановки узагальнених змінних (2.17) шукане критеріальне рівняння (2.9) для ВУП порошкового матеріалу М2 на ІВПМ матиме вигляд
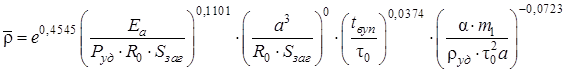 . (2.29)
. (2.29)
Аналогічно визначені показники степенів критеріальних рівнянь для процесів ВУП порошкових матеріалів М1, М3 та М4. Значення цих показників приведені у табл. 2.3. Постійні Аі, що відображують впливи на процес ВУП неврахованих факторів, в критеріальних рівняннях подані у вигляді Аі =еΘі.
Користуючись критеріальними рівняннями для процесів ВУП заготовок виробів з різних порошкових матеріалів на ІВПМ можна розв’язувати задачі оптимізація умов їх реалізації.
Таблиця 2.2 – Умови експериментального дослідження
| Рівні УП | Інтервал варіювання (Δ) | Нижній рівень (Н) | Верхній рівень (В) | Основний рівень (О) | |
|
Незалежні узагальнензмінні (УП) або визначальні критерії подібності |
π2 | 4,5906 | 0,6472/(1,6530)* | 5,2378 | 2,9425 |
| y1=lnπ2 | 1,1533097 | (-0,4351)**/ 0,5025918 | 1,6559015 | 1,0792575 | |
| π3 | 6,062·10-6 | 6,1261·10-6/ (6,8798·10-6) | 12,1881·10-6 | 9,1571·10-6 | |
| y1=lnπ3 | 0,57187 | (-12,002952)/ -11,886921 | 11,315051 | -11,600981 | |
| π4 | 0,8·103 | 0,6·103/ (0,7142·103) | 1,4·103 | 103 | |
| y1=ln4 | 0,6730645 | (6,3969296)/ 6,571163 | 7,2442275 | 6,9077553 | |
| π5 | 9,6·103 | 3,2·103/ (5·103) | 12,8·103 | 8·103 | |
| y1=ln5 | 0,9400072 | (8,00709062)/ 8,5171932 | 9,4572004 | 8,9871968 | |
Примітки:
1. В дужках в знаменнику наведений нижній рівень фактора πі після корегування;
2. В дужках в чисельнику наведений нижній рівень фактора yі=lnπі без корегування.
Таблиця 2.3 – Показники степенів критеріальних рівнянь для досліджуваних процесів ВУП
| Порошковий матеріал | Показники степенів | ||||
|
|
|
|
|
|
|
| М1 | 0,3121 | 0,2721 | (+0,016) | 0,0625 | -0,0714 |
| М2 | 0,4545 | 0,1101 | (-0,0217) | 0,0374 | -0,0723 |
| М3 | 0,4832 | 0,1208 | -0,0324 | 0,0481 | -0,0829 |
| М4 | 0,5877 | 0,1492 | -0,0401 | 0,0990 | -0,0653 |
Таблиця 2.4 – Матриця планування та результатів ПФЕ 24 (процес ВУП матеріалу М2)
| № дос-ліду | у0 | у1 | у2 | у3 | у4 | Середній відгук по 3-х точках | Серед. Відгук по 3-х точк. уэ | Оцін-ка lnπ1 за рівн. | Дис-персія для рядка Sи2 | (ут–уe)2 | |
| ρзср, г/см3 | ρ=ρзср/ρз0 | ||||||||||
| 1 | + | + | + | + | + | 2,2 | 1,6296 | 0,4883 | 0,469 | 0,0020 | 3,6·10-4 |
| 2 | + | – | + | + | + | 1,7 | 1,2592 | 0,2305 | 0,337 | 0,0355 | 112·10-4 |
| 3 | + | + | + | + | + | 2,4 | 1,7777 | 0,5753 | 0,481 | 0,0073 | 88·10-4 |
| 4 | + | – | – | + | + | 1,8 | 1,3333 | 0,2877 | 0,349 | 0,0234 | 37·10-4 |
| 5 | + | + | + | + | + | 2,0 | 1,4814 | 0,3930 | 0,444 | 0,0026 | 26·10-4 |
| 6 | + | – | + | - | + | 1,9 | 1,4074 | 0,3418 | 0,312 | 0,0050 | 19·10-4 |
| 7 | + | + | – | - | + | 2,2 | 1,6296 | 0,4884 | 0,456 | 0,0170 | 10·10-4 |
| 8 | + | – | – | - | + | 1,7 | 1,2592 | 0,2305 | 0,324 | 0,0370 | 86·10-4 |
| 9 | + | + | + | + | - | 2,7 | 2,0000 | 0,6931 | 0,537 | 0,0021 | 243·10-4 |
| 10 | + | – | + | + | - | 2,1 | 1,5555 | 0,4418 | 0,405 | 0,0150 | 14·10-4 |
| 11 | + | + | – | + | - | 2,8 | 2,0741 | 0,7295 | 0,549 | 0,0016 | 324·10-4 |
| 12 | + | – | – | + | - | 2,2 | 1,6296 | 0,4884 | 0,417 | 0,0270 | 50·10-4 |
| 13 | + | + | + | – | - | 2,3 | 1,7037 | 0,5328 | 0,562 | 0,0063 | 9·10-4 |
| 14 | + | – | + | – | - | 1,9 | 1,4074 | 0,3418 | 0,430 | 0,0254 | 77·10-4 |
| 15 | + | + | – | – | - | 2,5 | 1,8518 | 0,6162 | 0,574 | 0,0208 | 18·10-4 |
| 16 | + | – | – | – | - | 2,0 | 1,4814 | 0,3930 | 0,442 | 0,0101 | 24·10-4 |
|
|
а0= 0,45 | а1= 0,1101 | а2= -0,0217 | а3= 0,0374 | а4= 0,0723 | ρср= 2,2 | ρср= 1,5925 | уэср= 0,4653 | Σ Sи2= 0,2381 | Σ(ут–уе)2=0,1 | |

 Назад
Назад Зміст
Зміст Вперед
Вперед

