4 РОЗРАХУНОК БАЛОК НА МІЦНІСТЬ ПРИ ПЛОСКОМУ ЗГИНІ

 

 

4.1 Теоретичні відомості і методичні вказівки

 

4.1.1 Геометричні характеристики плоских поперечних перерізів

 

При деформації плоского  згину балки необхідно враховувати геометричні характеристики плоских поперечних перерізів.

Добуток площі dS (рис. 4.1) на відстань її від деякої осі називається елементарним моментом площі відносно осі. Тоді, складаючи елементарні моменти по всій площі поперечного перерізу, отримаємо

 

 

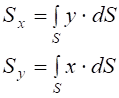
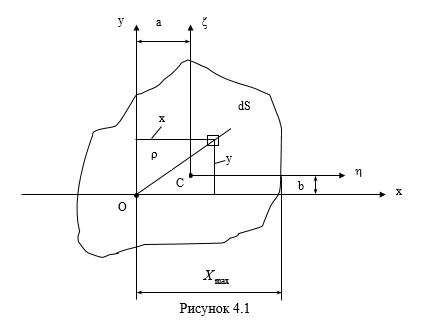
Статичні моменти площі 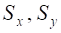 використовуються при визначенні центра ваги поперечного перерізу

 

,

 

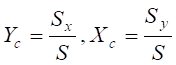де S – площа поперечного перерізу.

 

Момент інерції поперечного перерізу відносно осей x і y знайдемо таким чином:

 

.

 

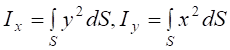При розрахунках на кручення використовується полярний момент інерції:

 

.

 

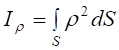У розрахунках на міцність зустрічаються з відношенням осьових моментів інерції до відстані точок, найбільш віддалених від відповідної осі (рис. 4.1).

 

,

 

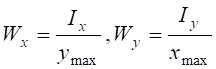де 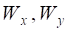 – осьові моменти опору відносно осей x та y.

 

Момент інерції поперечного перерізу відносно осі, що не проходить через центр маси С знаходиться за формулою.

 

.

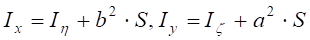де  І_η, І_ζ – моменти інерції поперечного перерізу тіла відносно центральних осей η і ζ (рис. 4.1).

Геометричні характеристики деяких плоских поперечних перерізів:

а) в формі прямокутника (рис.4.2);

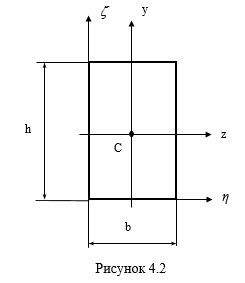
Моменти інерції поперечного перерізу відносно осей z, y, η та ζ

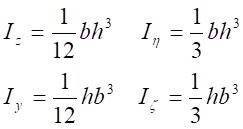
      Моменти опору поперечного перерізу відносно осей  z та y

 

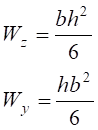
б) в формі круга (рис. 4.3);

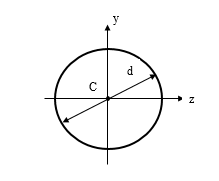
Рисунок 4.3

Моменти інерції поперечного перерізу відносно осей z і y та полярний момент інерції відносно центра мас С

 

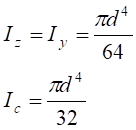
Моменти опору поперечного перерізу відносно осей z і y та центра  мас С