3.1.5 Приклад побудови епюр Q і М для балок

 

Побудуємо епюри поперечних сил і згинальних моментів для балки, показаної на рис. 3.6, а.

 

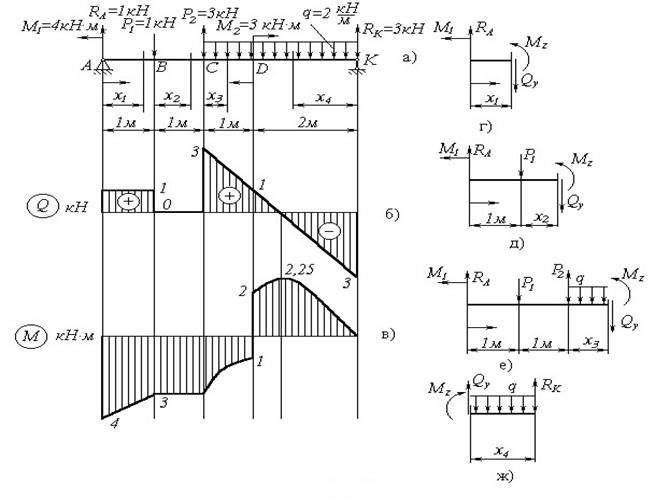
Рисунок 3.6

 

Розв’язання

Спочатку визначимо реакції опор R_A i R_K із рівнянь рівноваги статики (в опорі А горизонтальна складова реакції R_A дорівнює нулю, оскільки в системі відсутні сили, що проектуються на вісь стержня):

 

SМ_А = 0;

M₁ – Р₁×1 + Р₂×2 – q×3(2 + 3/2) – M₂  + R_к×5 = 0;

 

SМ_А  ;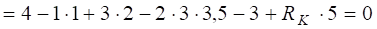

R_к = 3 кН.

 

SМ_К  = 0;

M₁ – R_А×5 + Р₁×4 – Р₂×3 – q×3(3/2) – M₂  = 0;

 

SМ_К  = ;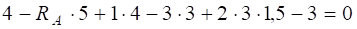

R_А = 1 кН.

 

Перевірка:

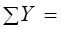     R_А – Р₁ + Р₂ – q×3  + R_к .

 

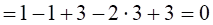Отже, реакції розраховані правильно.

Розділяємо балку на чотири ділянки і складаємо рівняння поперечних сил та згинальних моментів для кожної з них.

Будуємо епюри Q_y i M_z для ділянки АВ. Для цього зробимо переріз m₁-n₁ на відстані х від опори А і розглянемо рівновагу відсіченої частини (рис. 3.6, г). Згинальний момент M_z  і поперечну силу Q_y в перерізі будемо зображати додатними.

Ділянка АВ: 0 £ x₁ £ 1 м.

 

Q_y(x₁)  = R_A = 1 кН;                                                                                   (3.2)

 

M_z (x₁) = R_A×x₁ - M₁ = x₁ - 4;                                                                     (3.3)

 

при x₁=0 м,    M_z (0) = -4 кН×м,

при x₁=1 м,    M_z(1) = 1-4 = –3 кН×м.    

Як видно із рівнянь (3.2) і (3.3) поперечна сила залишається сталою на всій довжині ділянки АВ, а згинальний момент змінюється за лінійним законом. Графіки цих залежностей показані на рисунках 3.6, б та 3.6, в. Додатні значення сили Q_y будемо відкладати вгору від базової прямої, а від’ємні - вниз. Епюри згинальних моментів будуємо на стиснутих волокнах. Тому вгору від базової лінії будемо відкладати в масштабі додатні значення згинального моменту, а вниз - від’ємні.

Вказівка. При побудові епюр згинальних моментів на розтягнутих волокнах додатні значення згинального моменту відкладаються вниз, а вверх – від’ємні).

Будуємо епюри М_z i Q_y для ділянки ВС. Для цього зробимо переріз m₂-n₂ і розглянемо рівновагу лівої відрізаної частини балки (рис. 3.6, д)

Ділянка ВС: 0 £ x₂ £ 1 м;

 

Q_y(x₂)  = R_A - P₁ = 1-1 = 0 кН;                                                       

 

M_z(x₂)  = R_A(1+x₂) - P₁x₂  - M₁ =  1(1+x₂)  - 1×x₂ - 4 =  –3 кН×м. 

 

Будуємо графіки епюри  Q_y і M_z  на ділянці ВС (риc. 3.6, б, в).

Із умов рівноваги лівої відсіченої частини балки знаходимо закони, за якими змінюються Q_y i M_z на ділянці CD.

Ділянка CD: 0 £ x₃ £ 1 м.

 

Q_y(x₃) = R_A - P₁ + P₂ - qx₃ = 3 – 2×x₃;                                              

 

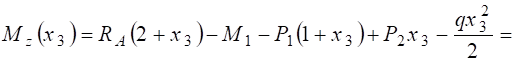 1(2 + x₃) – 4 – 1 (1 + +x₃) + 3x₃ – 2×x₃²/2 = -3 + 3x₃ – x₃² ;

 

при x₃ = 0 м,   Q_y(0) = 3 кН; M_z(0) = -3 кН×м;

при x₃ = 1 м,   Q_y(1) = 1 кН; M_z(1) = -1 кН×м.

Для побудови епюр Q_y i M_z на ділянці DK розглянемо рівновагу правої відрізаної частини балки (переріз m₃-n₃ , рисунок 3.6, е)

Ділянка DK: 0 £ x₄ £ 2 м.

 

Q_y(x₄)  = q×x₄-R_K = 2x₄-3;                                                                          (3.4)

 

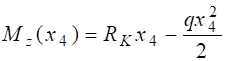= 3x₄ – x₄² ;                                                          (3.5)

 

при x₄ = 0 м,   Q_y(0) = –3 кН; M_z(0) = 0 кН×м;

при x₄ = 2 м,   Q_y(2) = 1 кН;  M_z(2) = 2 кН×м.

Епюра Q_y(x₄)  перетинає вісь х, (рис. 3.6, б), це означає що в точці перетину момент M_z набуде екстремального значення. Знайдемо цю точку із умови

 

Q_y(x₄) = 0,  або  2x₄-3 = 0, звідки 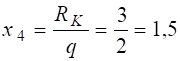   м.

 

Величина згинального моменту при х₄ = 1,5 м,

 

M_z (1,5) = 3x₄ – x₄²  = 3×1,5 – 1,5²  = 2,25 кН×м.

 

Будуємо епюри Q_y i M_z на ділянці DK (рис. 3.6, б, в).

Як видно із рисунків 3.6, б і в на ділянках, де немає розподіленого навантаження (q=0), поперечна сила Q_y залишається сталою, а момент M_z змінюється за лінійним законом (ділянка АВ). На ділянці ВС Q_y=0, а M_z=const. На ділянках CD та СК з рівномірно розподіленим навантаженням (q=const), епюра Q_y - лінійна (3.4), а згинальний момент M_z змінюється за законом квадратичної параболи (3.5).

Оскільки епюра M_z побудована на стиснутих волокнах, то опуклість параболи звернена в бік протилежний напрямку дії навантаження q (ділянки CD та СК).

Вказівка. При побудові епюр згинальних моментів на розтягнутих волокнах опуклість параболи звернена в бік, що збігається з напрямком дії навантаження q).

В перерізах, де прикладені зосереджені сили, на епюрі Q_y мають місце стрибки на величину цих сил в напрямку вектора сили, а на епюрі M_z - злами.

В перерізах, де прикладені тільки зосереджені моменти, на епюрі Q_y змін немає, а на епюрі M_z мають місце стрибки на величину цих моментів.

На ділянках, де Q_y = 0, момент M_z сталий, а в перерізах, де Q_y = 0, згинальний момент набуває екстремального значення.

 

Питання для самоперевірки знань

та контролю засвоєння матеріалу

 

1. Види навантажень на тіла.

2. Внутрішні та зовнішні сили.

3. Як визначаються внутрішні сили?

4. Правило знаків при визначенні внутрішніх сил.

5. Чи залежать внутрішні сили в тілах від зовнішніх?

6. Дати означення видів внутрішніх сил..

7. Методика визначення внутрішніх зусиль..