
|
ТЕОРЕТИЧНА ТА ПРИКЛАДНА МЕХАНІКА
|

|
ТЕОРЕТИЧНА ТА ПРИКЛАДНА МЕХАНІКА
|
4.2 Завдання для самостійної та індивідуальної роботи. Розрахунок балок на міцність при плоскому згині
Приклад:Для балки ( задачі 1 – 30, підрозділ 2.3) при α = 0 побудувати епюри згинальних моментів та поперечних сил і на підставі епюри згинальних моментів М підібрати стальну балку прямокутного (рис. 4.2) поперечного профілю (h=2b) при [s]=160 МН/м2 .
Рисунок 4.5 Розв’язання Розглянемо просту балку на двох опорах (рис. 4.5, а): опора А – нерухомий шарнір; опора В – рухомий шарнір. Дію в’язей (шарнірів) на балку замінюємо реакціями в’язей Перевірка: Балка має чотири ділянки, тому проводимо чотири довільні перерізи (рис. 4.5, а) і знаходимо поперечну силу Qі та згинальний момент Мі у кожному перерізі. Переріз I-I: при при Переріз II-II : при при Переріз III-III: при при Переріз IV-IV: при при За отриманими даними Qі та Мі (і=1,2,3,4) будуємо епюри Q (рис. 4.5, б) та М (рис. 4.5, в). Ординати Qі та Мі відкладаємо перпендикулярно до осі балки. Для поперечної сили Qі додатні значення відкладаємо над базовою лінією (відносно балки), а епюру Мі будуємо на розтягнутих волокнах. Розміри поперечного перерізу балки будемо знаходити із умови міцності (4.12) де Так як за умовою h=2b, то Знайдемо мінімальне значення ширини b поперечного профілю балки: де Відповідь: приймаємо b=60мм, h=120мм.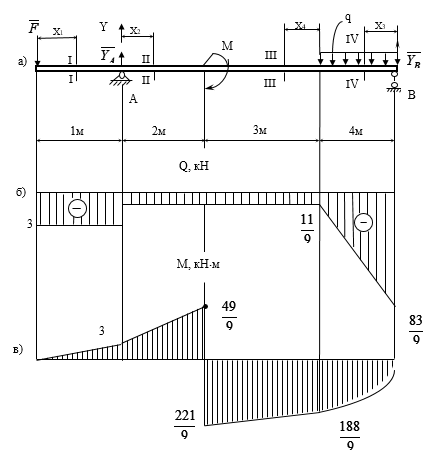
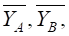 які знаходимо з рівнянь рівноваги при F=3кН, q=2кН/м, М=30кН×м
які знаходимо з рівнянь рівноваги при F=3кН, q=2кН/м, М=30кН×м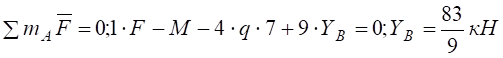 ,
,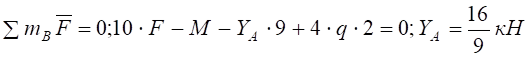 .
.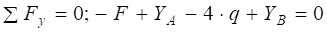 ,
,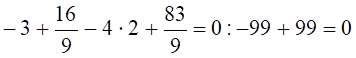 .
.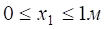
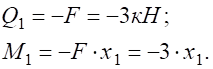
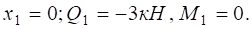
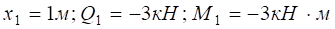 .
.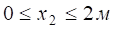
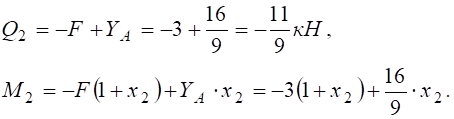
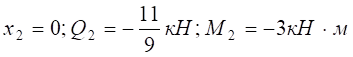 .
. 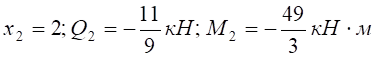 .
.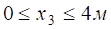
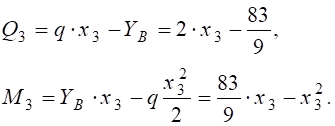
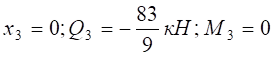 .
.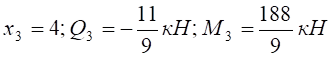 .
.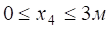
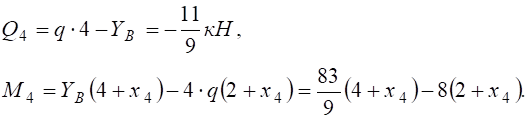
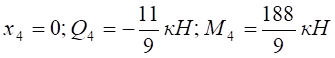 .
.
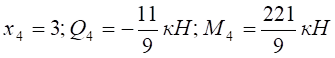 .
.
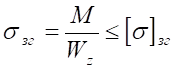 ,
,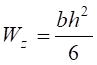 – момент опору.
– момент опору.
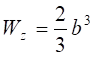 .
.
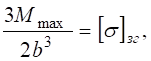
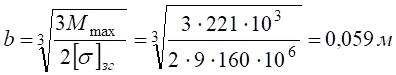 ,
,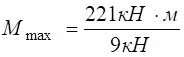 – максимальне значення згинального моменту (рис. 4.5, в).
– максимальне значення згинального моменту (рис. 4.5, в).