5 КІНЕМАТИКА ТОЧКИ

5.1 Теоретичні відомості і методичні вказівки

При координатному способі завдання руху точки М (рис. 5.1) її положення  у просторі, використовуючи декартову систему координат, Oxyz задається трьома функціями:

, , .

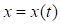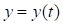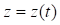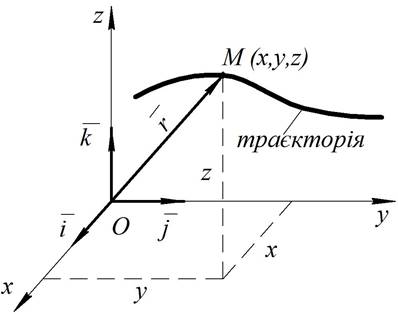
Рисунок 5.1

Проекції вектора швидкості на координатні осі знаходять за формулами

, , ,

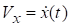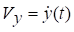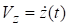а вектора прискорення

, , .

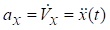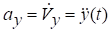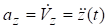За цими формулами можна обчислити: траєкторію руху  точки, проекції швидкостей і прискорення у будь-який заданий момент часу. Величини швидкості та прискорення точки М, спрямовуючи косинуси векторів швидкості і прискорення обчислюються наступним чином:

,

,

;;,

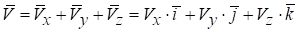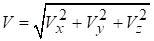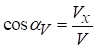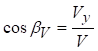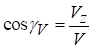де α_V, β_V, γ_V ‑ відповідні кути між вектором швидкості 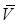 і відповідною віссю.

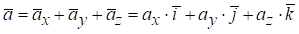
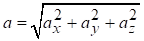 ‑ модуль прискорення точки,

де a_x, a_y, a_z  ‑ проекції вектора прискорення на вісі x, y, z.

;;,

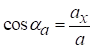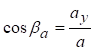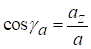де α_а, β_а, γ_а ‑ відповідні кути між вектором прискорення 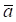 і відповідною віссю.

Проекції прискорення вектора прискорення точки на дотичну та нормальні осі натуральних осей координат знаходяться за формулами:

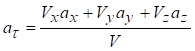 ‑ дотичне прискорення, що характеризує зміну швидкості за величиною і завжди спрямоване вздовж дотичної до траєкторії в точці;

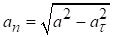 ‑ нормальне прискорення, яке напрямлене в бік угнутості траєкторії до центра кривизни і характеризує зміну швидкості за напрямком.

Радіус кривизни траєкторії в даній точці: .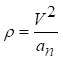

Питання для самоперевірки знань

та контролю засвоєння матеріалу

1. Які кінематичні способи завдання руху точки?

2. Чому дорівнює проекція швидкості точки на дотичну до її траєкторії та модуль її швидкості?

3. Як визначаються проекції швидкості та прискорення точки на нерухомі вісі декартових координат?

4. В який момент часу нормальне прискорення при криволінійному русі дорівнює нулю?