1.2 Сутність і принципи системного підходу. Поняття системи
Теорія систем і системного аналізу, у загальному випадку, як галузь науки, може бути розділена на дві, причому досить умовні, частини:
– теоретичну, що використовує такі галузі як теорія ймовірностей, теорія інформації, теорія ігор, теорія графів, теорія розкладів, теорія рішень, топологія, факторний аналіз і таке інше;
– прикладну, що заснована на прикладній математичній статистиці, методах дослідження операцій, системотехніці і т.п. Таким чином, ТССА широко використовує досягнення багатьох галузей науки і це «охоплення» безупинно розширюється.
Разом з тим, теорія систем має власне «ядро», тобто, свій особливий метод – системний підхід до задач, що виникають. Сутність цього методу досить проста: всі елементи системи і всі операції в ній повинні розглядатися лише як одне ціле, і не у сукупності, а у взаємозв’язку.
Невдалий досвід багатьох спроб вирішити системні питання з ігноруванням цього принципу, тобто спроб використання "містечкового" підходу досить добре вивчений і показує, що локальні рішення, врахування недостатнього числа факторів, локальна оптимізація – на рівні окремих елементів майже завжди приводили до неефективного, у цілому, а іноді і небезпечного за наслідками, результату. Отже:
- Перший принцип ТССА – це вимога розглядати сукупність елементів системи як одне ціле або, більш жорстко, – заборона розглядати систему як просте об’єднання елементів;
- Другий принцип полягає у визнанні того, що властивості системи є не просто сумою властивостей її елементів. Тобто, Вона характеризується особливими властивостями, які можуть і не мати окремі її елементи.
- Важливим атрибутом системи є її ефективність. Теоретично доведено, що завжди існує функція цінності системи – у вигляді залежності її ефективності (це майже завжди економічний показник) від умов побудови і функціонування. Крім того, ця функція обмежена, а значить можна і потрібно шукати її максимум. Максимум ефективності системи може вважатися третім основним принципом.
- Четвертий принцип забороняє розглядати систему окремо від навколишнього середовища, тобто як автономну, відособлену. Це означає обов’язковість врахування зовнішніх зв’язків або вимогу розглядати досліджувану систему як частину (підсистему) деякої більш загальної системи.
- З урахуванням четвертого принципу приходимо до п’ятого принципу – можливості (а іноді і необхідності) декомпозиції системи на частини, підсистеми. Якщо останні виявляються недостатньо простими для аналізу, то до них застосовується цей самий принцип. Однак в процесі такої декомпозиції не можна порушувати попередні принципи. Поки вони дотримаються, декомпозиція виправдана, тобто дозволена в тому сенсі, що гарантує можливість застосування практичних методів, прийомів, алгоритмів розв’язання задач системного аналізу.
- Усе вищесказане дозволяє формалізувати визначення терміну система. Системою є багаторівнева конструкція взаємодіючих елементів, що поєднуються у підсистеми декількох рівнів, з точки зору досягнення єдиної мети її функціонування (деякої цільової функції).
Класифікація систем
Складні і прості системи. Однією з характерних тенденцій розвитку суспільства на даний час є поява великих і надзвичайно складних систем (великі автоматизовані, технологічні, енергетичні, гідротехнічні, інформаційні й інші комплекси). З іншого боку прагнення пізнати світ, у якому живе людство, як складну багатофункціональну систему стало реальністю сьогоднішнього дня. Усе це призвело до необхідності визначити поняття складної системи, розробити методичні принципи її дослідження, керування і проектування.
На даний час однозначного, чіткого означення складної системи немає. Відомі різні підходи і запропоновані різні формальні ознаки її означення. Так, наприклад, Г. Н. Поворов пропонував відносити до складних системи, що характеризуються великим числом (104 -107 і більше) елементів. Недолік такого підходу полягає у тому, що дане означення складності є відносним, а не абсолютним.
Англійський кібернетик С. Бор пропонує до складних відносити системи, які описуються мовою теоретико-імовірнісних методів (мозок, економіка, форма і т.п.).
Найчіткішим, на наш погляд, є таке означення складних систем.
Означення: Складною системою називається система, у моделі якої недостатньо інформації для ефективного керування цією системою.
Таким чином, ознакою простоти системи є достатність інформації для її керування. Якщо ж результат керування, отриманий за допомогою моделі, буде несподіваним, то таку систему відносять до складної.
Для занесення системи в розряд проста необхідно отримати відсутню інформацію про неї і включити її в модель.
Від складних систем необхідно відрізняти великі системи.
Означення: Система, для актуалізації моделі якої з метою керування бракує матеріальних ресурсів (машинного часу, ємності пам’яті, інших матеріальних засобів моделювання) називається великою.
До таких систем відносяться, наприклад, економічні, організаційно-управлінські, нейрофізіологічні, біологічні і т.п. системи.
Способом переводу великих систем у прості є створення нових потужніших засобів обчислювальної техніки.
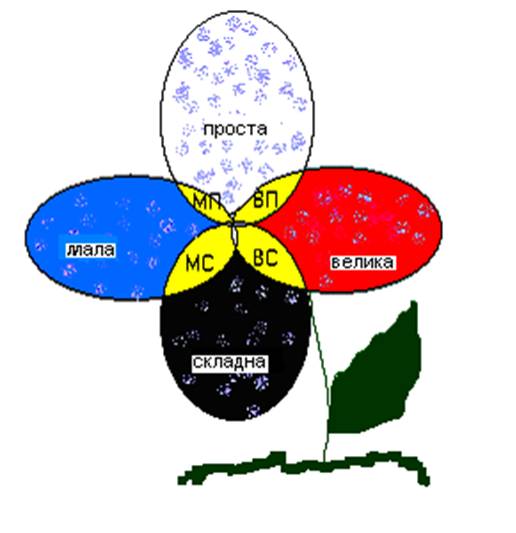
Як видно з наведених означень, поняття великої і складної системи є різними. Однак у літературі ці поняття визначені не однозначно. Деякі автори взагалі не використовують цих понять, інші використовують їх як синоніми, а деякі вважають різницю між ними лише кількісною. Для того, щоб ще раз підкреслити різницю між поняттями «велика» і «складна» системи наведемо приклади , що подані у табл. 1.1.
У наведеній таблиці знаком «+» розпізнані класифікаційні ознаки систем. Пояснимо, наприклад, чому шифрозамок віднесено до класу великих і простих систем. Ця система – велика, оскільки у викрадача може не вистачити ресурсу часу для розкриття замка, а також і проста – оскільки розкриття зводиться до простого перебору шифрів.
| № | Система | Мала | Велика | Проста | Складна |
|---|---|---|---|---|---|
| 1 | Справний побутовий прилад для користувача | + | + | ||
| 2 | Несправний побутовий прилад для майстра | + | + | ||
| 3 | Шифрозамок для викрадача | + | + | ||
| 4 | Мозок, живий організм | + | + |
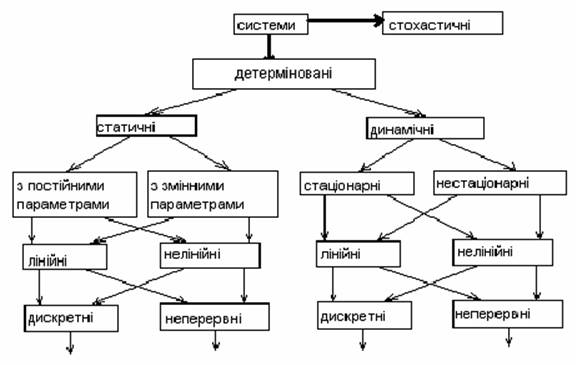
На рис. 1.1 ілюструються можливі сполучення ознак систем.
Класифікація систем за їх основними властивостями. Наведена нижче класифікація має принципово важливе значення, оскільки вона використовується для побудови математичних моделей систем. Відповідно їй системи можуть бути класифіковані за такими ознаками.
Динамічні системи характеризуються тим, що їх вихідні сигнали на даний момент часу визначаються характером вхідних впливів у минулому (залежать від передісторії). Інакше, системи називають статичними.
Прикладом динамічних систем можуть бути біологічні, економічні, соціальні системи і такі штучні системи як завод, підприємство, поточна лінія і т.д.
Детермінованною називають систему, якщо її роботу можна абсолютно точно передбачити. Системи, стани яких залежать не тільки від контрольованих, але і від неконтрольованих впливів або якщо в них самих знаходиться джерело випадковості, називають стохастичними. До стохастичних систем можна віднести, наприклад, заводи, аеропорти, мережі і системи ЕОМ, магазини, підприємства побутового обслуговування та інші.
Розрізняють системи лінійні і нелінійні. Для лінійних систем реакція на суму двох чи більше різних впливів еквівалентна сумі реакцій на кожне збурювання окремо, для нелінійних – це не виконується.
Якщо параметри систем змінюються у часі, то вони називаються нестаціонарними. Протилежним поняттям є поняття стаціонарних систем.
Приклад нестаціонарних систем – це системи, де процеси, наприклад, старіння є на даному інтервалі часу істотними.
Якщо вхід і вихід системи вимірюється чи змінюється в часі дискретно, через крок t, то система називається дискретною. Протилежним поняттям є поняття неперервної системи. Наприклад: ЕОМ, електронні годинник, електролічильник – дискретні системи; пісковий годинник, сонячний годинник, нагрівальні прилади і т.д. – неперервні системи.
На рис. 1.2 наведена класифікація систем за їх властивостями, де стрілки вказують можливий набір властивостей систем.