2.3 Основні етапи математичного моделювання
Для побудови математичних моделей конкретних задач системного аналізу можна рекомендувати таку послідовність робіт:
- вивчення умови задачі (предметної області);
- визначення найважливіших факторів;
- виділення відомих і невідомих параметрів;
- виявлення керованих і некерованих параметрів;
- доповнення умови задачі відсутніми відомостями;
- введення системи позначень;
- побудова математичної моделі задачі (математичний опис найважливіших факторів, співвідношень і зв’язків між параметрами).
Розглянемо наведені етапи моделювання на конкретних прикладах.
Приклад 2.1. Планування добового випуску продукції. Процес виготовлення виробів двох типів полягає у послідовній обробці кожного з них на трьох верстатах. Нам відомі: час експлуатації кожного верстата за добу, час обробки одиниці кожного виробу на кожному верстаті, вартість реалізації одиниці кожного виробу. Потрібно скласти план добового випуску виробів таким чином, щоб дохід від їх продажу був максимальним.
Під час аналізу найважливіших факторів будемо виходити тільки з умови поставленої задачі, відповідно яким:
– ОПР – орган планування фірми;
– мета – досягнення максимуму прибутку від продажу випущених за добу виробів двох видів;
– прийняття рішення для ОПР полягає у визначенні добових обсягів випуску кожного з двох видів виробів;
– можливості ОПР обмежені часовими ресурсами експлуатації верстатів трьох видів;
– про інші обмеження або умовах у задачі нічого не говориться.
Після виявлення найважливіших факторів слід аналізувати всі параметри задачі: значення яких параметрів відомо (задано); які параметри є невідомими (шуканими) величинами; якими з параметрів ми можемо керувати (керовані змінні), а якими немає (некеровані параметри).
У наведеному прикладі відомими є такі параметри:
– добова норма b1 експлуатації верстата 1;
– добова норма b2 експлуатації верстата 2;
– добова норма b3 експлуатації верстата 3;
– час aij обробки одиниці виробу виду i на верстаті типу j;
– вартість с1 (продажу) одиниці виробу виду 1;
– вартість c2 (продажу) одиниці виробу виду 2;
Усі ці параметри є некерованими, оскільки вони задані (їх значення можна знайти в довідниках або нормативах, визначити з минулого досвіду). Шуканими ж є такі величини:
– обсяг добового випуску виробу виду 1;
– обсяг добового випуски виробу виду 2.
Ці два параметри можна вважати керованими, оскільки фірма сама визначає їх величину, виходячи з реальних умов.
Далі для складання математичної моделі задачі потрібно ввести систему позначень невідомих параметрів задачі. Для нашого прикладу зробимо такі позначення:
x1 – обсяг добового випуску одиниць виробу виду 1;
x2 – обсяг добового випуску одиниць виробу виду 2.
Тоді прибуток від продажу x1 і x2 буде визначатися як c1 x1 + c2 x2, а час, що необхідний для обробки x1, x2 одиниць виробів на верстаті j – як
aij x1 + a2j x1, (j = l, 2, 3),(2.8)
Тепер поставлену задачу можна сформулювати математично:
c1 x1 + c2 x2 → max,(2.9)
a11 x1 + a21 x2 ≤ b1,(2.10)
a12 x1 + a22 x2 ≤ b1, (2.11)
a13 x1 + a23 x2 ≤ b1,(2.12)
x1 ≥ 0, x2 ≥ 0.(2.13)
Умови невід’ємності змінних випливає з того, що величини x1 і x2 – це доповнення моделі, хоча і відсутньою, однак, очевидною інформацією.
Наведений запис і є задачею математичного програмування з цільовою функцією c1 x1 + c2x2 і множиною допустимих рішень X, що описується п’ятьма нерівностями (на площині це багатокутник, що утворений перетинанням п’яти півплощин).
У наведених нижче прикладах побудови моделей простежте етапи математичного моделювання, які ми виконаємо без коментарів (див. з цього приводу Приклад 2.1).
Приклад 2.2. Розміщення замовлень. Фірма отримала замовлення на кілька тисяч нових виробів, що збираються з окремих блоків. Керівництво фірми прийняло рішення розмістити замовлення на виготовлення n блоків і вибрало nфірм-постачальників. Кожне замовлення настільки велике, що фірма-постачальник не може виконати більш одного замовлення. Кожному постачальнику запропоновано визначити вартість виконання замовлення, тобто ціну, по якій він готовий поставити фірмі різні блоки. Фірма повинна укласти n контрактів на постачання їй n видів блоків, мінімізувавши при цьому свої загальні витрати на придбання комплектуючих вузлів з боку.
Позначимо: i – номер (назва) блоку, i = 1,...,n; j – номер (назва) фірми-постачальника, j = 1,...,n; сij - вартість виконання i-ro блоку j-ої фірми (задане число). Крім того, введемо для кожного i та j число
(2.14)
Цільова функція, що має зміст загальних витрат на покупку комплектуючих блоків, запишеться таким чином
, (2.15)
Обмеження задачі (на змінні хij) мають такий зміст:
– кожен i-й блок повинен бути виконаний;
– кожен j-й постачальник повинен виконати один який-небудь блок .
Математично ці умови запишуться відповідно як:
xi1+xi2 +…+xin = 1, xij + x2j+…+ xnj =1,(2.16)
Таким чином, приходимо до такої задачі оптимізації (моделі):
(2.17)
(2.18)
Приклад 2.3. Вибір портфеля цінних паперів. Фахівцю з фінансового аналізу, що працює в банку (або в страховій компанії) потрібно визначити найкращий набір акцій, облігації та інших цінних паперів на виділену суму з метою мінімізації ризику, пов’язаного з придбанням набору цінних паперів. Прибуток до кінця планового періоду на кожен долар, вкладений у папір j-го виду, характеризується двома показниками: аj – фактичний прибуток (випадкове число), αj – очікуваний прибуток. Потрібно, щоб очікуваний прибуток на долар інвестицій був для всього набору цінних паперів не нижче заданої величини b.
Для визначення моделі приймемо всі фонди, що виділені для придбання цінних паперів, рівними одиниці і позначимо через xj – частку від усіх фондів, що виділяються для придбання цінних паперів виду j. Ризик враховується за допомогою коваріації σij = М (аi – αi) (аj – αj) прибутку для цінних паперів виду i і виду j (термін з теорії ймовірностей). Математична модель, при цьому, запишеться як
(2.19)
за обмежень:
xj ≥ 0, j = 1,…,n, (2.20)
де n – число різновидів цінних паперів.
Цільова функція має сенс дисперсії фактичного прибутку (розсіювання фактичного прибутку від очікуваної), перше обмеження є умова на очікуваний прибуток, а останнє – не перевищення фондів, виділених на покупку цінних паперів.
Приклад 2.4. Задача про рекламу. Фірма планує проведення радіо-рекламної кампанії по збуті автомобілів в одному з регіонів, де розташовано s радіостанцій, протягом двох тижнів. Фірма оцінила попередньо, що якщо радіостанції j виділити уj доларів, то чистий прибуток від збільшення збуту дорівнює Rj(yj) (Rj – функція реалізації прибутку від обсягу фінансування реклами). На рекламу виділена сума у N доларів. Число рекламних оголошень на день не повинно перевищувати M. Якщо фірма виділила j-ій радіостанції уj доларів, то число рекламних оголошень буде Kj(yj) (Kj – функція, що кожній виділеній сумі ставить у відповідність кількість рекламних оголошень на день, і вважається відомою). Як потрібно фінансувати s радіостанцій, щоб отримати сумарний максимальний прибуток від реакції збуту на рекламу ?
Очевидно, що математична модель буде мати вигляд:
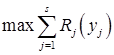 , (2.21)
, (2.21)
за обмежень:
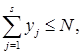
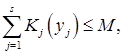 yj ≥ 0, j = 1, …, s, (2.22)
yj ≥ 0, j = 1, …, s, (2.22)
Приклад 2.5. Задача керування виробництвом. Фірма повинна розробити календарну програму випуску деякого виду виробів на плановий період, що складається з Т відрізків (тижнів, місяців, кварталів, років). Передбачається, що для кожного з цих відрізків є точний прогноз попиту на продукцію, що випускається. Час виготовлення партії виробів настільки малий, що їм можна зневажити. Для різних відрізків попит неоднаковий, крім того, на економічні показники виробництва впливають обсяги виготовлених партій. Збереження запасів, що виникають при цьому, (перевищення випуску над попитом на деяких відрізках) пов’язано з визначеними витратами. Потрібно розробити таку програму, за якою загальна сума витрат на виробництво і зміст запасів буде мінімальною за умови повного задоволення попиту на продукцію.
Позначимо через:
xt – випуск продукції протягом деякого відрізка t;
yt – рівень запасів на кінець відрізка t;
Dt – попит на продукцію для відрізка t;
Витрати на відрізку t (позначимо їх через Сt) залежать від випуску xt і рівня запасів yt, тобто є функцією від цих невідомих величин ct = ct (xt, yt).
Вимога задоволення попиту в межах кожного часового відрізка означає, що рівень запасів на кінець відрізка t (тобто yt) повинен дорівнювати сумі рівня запасів на початок відрізка t (тобто yt-1) і випуску продукції на відрізку t (тобто xt) мінус попит на відрізку t (тобто Dt).
Звідси отримуємо таку модель:
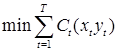 , (2.23)
, (2.23)
за обмежень:
уt–1 + xt – yt = Dt, t = 1, 2, …, T; yТ = 0, xt, yt ≥ 0 для всіх t, (2.24)
де y0 – заданий рівень запасів на початок планового періоду, а yТ – рівень запасу на кінець періоду.
Приклад 2.6. Оптимізація схеми обслуговуванн). Система обслуговування складається з n типів різних приладів (наприклад каси в магазинах, телефонні лінії, автозаправні стовпчики та інші.). Кожен прилад у будь-який момент часу обслуговує не більш однієї заявки (наприклад покупця, телефонної розмови, автомобіля та інші.). Відома кількість приладів j-го типу і число заявок i-го типу, що прибули в систему на момент часу t. Відома також ефективність j-го приладу під час обслуговування заявки i-го виду. Потрібно розподілити вільні прилади за заявками таким чином, щоб сумарна ефективність була найбільшою.
Для побудови моделі спочатку введемо позначення вільних величин:
Nj – кількість приладів j-го типу;
dit – число заявок i-го типу на момент часу t;
μij – ефективність j-го приладу при обслуговуванні заявки i-го виду.
Позначимо шукану величину через xij – число приладів j-го виду, відведених для обслуговування заявок i-го типу. Цих даних досить для побудови математичної моделі вигляду:
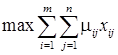 , (2.25)
, (2.25)
за обмежень:
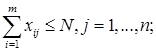
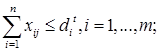 (2.26)
(2.26)
де xij – цілі невід’ємні числа для всіх i, j;
m і n задані числа кількості видів заявок і приладів.
Приклад 2.7. (Вибір оптимального виду посівної культури). Фермер може посіяти одну з трьох культур: A1, А2 або А3. Врожаї цих культур багато в чому залежать від погоди. Потрібно визначити, яку з цих культур сіяти, щоб забезпечити найбільший прибуток, якщо відома ціна аi одного центнера культури Ai, i = 1, 2, 3, і середня врожайність кожної культури залежно від погоди (літо буде посушливим, нормальним або дощовим). Достовірний прогноз погоди відсутній.
Позначимо через hij – врожайність i-ої культури за погодних умов j (тут j = 1 – літо посушливе, j = 2 – нормальне літо, j = 3 – дощове літо). Числа hij, як і числа ai задані і відомі. Реально може мати місце тільки одна із ситуацій (i, j), i = l, 2, 3; j = l, 2, 2. Причому (i, j) означає, що посіяно культуру Aj, а погода знаходиться у стані j. Усього таких ситуацій дев’ять. Очевидно, що фермер може вибрати тільки вид культури (стан погоди від нього не залежить). Якщо фермер засіяв культуру A1, то він може отримати (залежно від погоди) один з таких прибутоків: a1h11, a1h12, a1h13, щодо культури A2: a2h21, a2h22, a2h23, і для культури А3: a3h31, a3h32, a3h33 .
Запишемо всі ці результати в одну таблицю (матриця А). Ця матриця і буде математичною моделлю вихідної задачі. У ній дія фермера зводиться до вибору одного з рядків матриці (однієї з трьох стратегій). Його прибуток залежить від "вибору" природою одного зі своїх станів (одного із трьох стовпців матриці). Наприклад, якщо фермер посіяв культуру A2, а літо вийшло дощовим, то прибуток фермера дорівнює a2h22.
(2.27)
Приклад 2.8. Вибір асортименту товарів. На базі торгової організації є n типів одного з товарів асортиментного мінімуму. У магазин повинен бути завезений тільки один з типів даного товару. Потрібно вибрати той тип товару, що доцільно завезти в магазин. Якщо товар типу j буде користатися попитом, то магазин від його реалізації дістане прибуток pj, якщо ж він не буде користатися попитом – то збиток qj. Скласти математичну модель цієї задачі в умовах невизначеного попиту. Керуючись формалізацією задачі прикладу 1.7, обґрунтуйте, що шукана модель має вигляд:
(2.28)
Поясніть задачу магазина на цій моделі.
Приклад 2.9. Планування оптимального терміну закінчення робіт. Компанія повинна реалізувати проект будівництва об’єкта, що складає з n операцій (робіт). Керівники комплексу оцінили тривалість виконання кожної операції та установили послідовність операцій, тобто точно визначили, які операції обов’язково повинні бути закінчені, щоб могла початися кожна з операцій, що входять у комплекс. Керівництву компанії треба з’ясувати, яка найменша можлива тривалість реалізації всього проекту, тобто найбільш ранній із усіх можливих термінів його завершення.
Під час побудови математичної моделі припустимо, що проект складається з п’яти операція А, В, С, D, Е. За умовою відома послідовність операцій і їх тривалість (табл. 2.1).
Фіктивна операція F, що починається в момент завершення проекту, вводиться для зручності (див. нижче). Другий стовпчик таблиці означає, що операцію С не можна почати, перш ніж незакінчена операція А і т.д.
| Операції | Безпосередньо попередні операції | Тривалість операцій |
|---|---|---|
| А | — | t |
| В | — | t |
| С | А | t |
| D | А | t |
| Е | B,D | tE |
| F | С,Е | — |
Приймемо, що змінними є терміни початку операції (введемо лише ті з них, що потрібні для рішення задачі):
yCD – момент початку операцій С і D;
yЕ – момент початку операції Е;
yF – момент початку операції F.
Тут, yF – момент завершення всього комплексу. Моменти yА і yВ – моменти 0 початку операцій, оскільки операції А і В не мають попередніх. При цьому математична модель має вигляд:
min yF, (2.29)
за обмежень:
yCD ≥ tA; yE ≥ tB; yE ≥ tD + yCD; yF ≥ tC + yCD; yF ≥ tE + yE , (2.30 – 2.34)