2.5 Моделювання систем в умовах визначеності
Класичним прикладом найпростішої задачі системного аналізу в умовах визначеності може бути задача виробництва і постачання товару. Нехай деяка фірма повинна виробляти і поставляти продукцію клієнтам рівномірними партіями у кількості N = 24000 одиниць за рік. Зрив постачань неприпустимий, оскільки штраф за це можна вважати нескінченно великим. Запускати у виробництво слід відразу всю партию (такі умови технології). Вартість збереження одиниці продукції Cx = 10 копійок на місяць, а вартість запуску однієї партії у виробництво (незалежно від її обсягу) складає Cp = 400 грн. Таким чином, запускати в рік багато партій явно невигідно, але й невигідно і випустити всього 2 партії в рік – занадто великі витрати на збереження! Скільки ж партій на рік найкраще буде випускати?
Побудуємо математичну модель такої системи. Позначимо через n розмір партії і знайдемо кількість партій за рік – p = N/n = 24000/n. Виходить, що інтервал часу між партіями складає t = 12/p (місяців), а середній запас виробів на складі – n/2 штук. Скільки ж нам буде коштувати випуск партії в n штук за один раз?
Підрахувати неважко – 0.1×12×n/2 гривень на складські витрати у рік і 400×p гривень за запуск партій з n штук виробів у кожній.
У загальному вигляді річні витрати складають
E = Cx T n / 2 + Cp N / n,(2.35)
де T = 12 – повний час спостереження у місяцях.
Таким чином, перед нами постає типова варіаційна задача: знайти таке n0, за яким сума E досягає мінімуму.
Розв’язок цієї задачі знайти зовсім просто – треба взяти похідну за n і прирівняти цю похідну до нуля. Це дає:
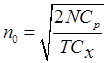, (2.36)
що для нашого прикладу складає 4000 одиниць в одній партії і відповідає інтервалу випуску партій величиною у 2 місяці. Витрати при цьому мінімальні і визначаються як:
, (2.37)
що для нашого прикладу складає 4800 гривень в рік.
Співставимо цю суму з витратами за умови випуску 2000 виробів у партії або випуску партії один раз на місяць з точки зору недобрих традицій соціалістичного планового господарства:
E1 = 0.1×12×2000/2 + 400×24000/ 2000 = 6000 гривень у рік.
Коментарі, як кажуть, – зайві!
Зазвичай, так просто розв’язувати задачі прийняття оптимальних стратегій вдається далеко не завжди, навіть якщо мова йде про детерміновані дані щодо опису життя системи – її моделі. Існує цілий клас задач системного аналізу і відповідних їм моделей систем, де мова йде про необхідність мінімізувати одну функцію багатьох змінних такого типу:
E = a1X1 + a2X2 + ... + anXn, (2.38)
де Xi – шукані змінні; ai – відповідні їм коефіцієнти або «ваги змінних» і, при цьому, мають місце обмеження як на змінні, так і на їх ваги.
Такі задачі добре досліджені у спеціальному розділі прикладної математики – лінійному програмуванні. Ще в докомп’ютерні часи були розроблено алгоритми пошуку екстремумів функцій E = f (a, X), які назвали – цільовими. Вони використовуються і зараз, і є основою для розробки прикладних програм системного аналізу. При цьому, системний підхід до розв’язання практичних задач керування, зокрема, для задач з багатьма змінних призвів до появи спеціалізованих типових напрямків як у області теорії аналізу, так і у практиці. «Найстарішими» і, отже, найперевіренішими є методи, що давно вже називають класичними. Фахівцям у галузі ділового адміністрування треба знати ці задачі хоча б на рівні постановки (див. підрозділ 2.1) і, головне, у плані моделювання відповідних систем.
Початки теоретичного обґрунтування і розробки практичних методів розв’язання задач лінійного програмування були покладені Д. Данцигом (за іншою версією – Л. В. Канторовичем). Для більшості конкретних додатків універсальним вважається так званий симплекс-метод. Для нього і супутніх йому методів розроблено багато спеціальних пакетів прикладних програм (ППП).